信息熵基础

信息熵

1. 熵

1.1 熵的定义

定义一个用来描述事件的不确定程度的量，即信息量，假设某一事件$x$发生的概率是$p(x)$,信息量为$I(x)$：

1. 当$p(x)=0$的时候，$I(x)=+\infty$;
2. 当$p(x)=1$的时候，$I(x)=0$
3. 当$p(x)<p(y)$的时候，$I(x)>I(y)$
4. $I(x)>=0$
5. 当事件相互独立的时候，联合概率密度$p(x,y)=p(x)p(y)$,信息量为$I(x,y)=I(x)+I(y)$.即独立事件同时发生的的信息量等于单个事件信息量之和

$$I(x)=-clog(p(x))$$

满足上面的性质，$c$是常数，对数的底数任意，于是就将$I(x)=-log(p(x))$，称作信息量。信息量的表达形式是人为设定的，用来满足一些对于信息量抽象概念的性质。

熵是用来描述一个系统的平均信息量的，即一个系统的平均不确定程度，假设某一系统(随机变量)由很多事件（观测值）$(x_0,x_1,....,x_{n-1})$构成，事件的概率分布为$(p(x_0),p(x_1),...,p(x_{n-1}))$,定义：

信息熵

$$H(x)=\sum_{i=0}^{n-1}p(x_i)I(x_i)=-\sum_{i=0}^{n-1}p(x_i)log(p(x_i))$$

1.2 熵的极大值定理证明：

一个随机变量的熵值在各个取值的概率都相等的时候取得最大（每个系统的熵是相对的，只有同一系统才能比较熵值的大小，不同的系统不能比较）

简化写为

$$H=-\sum_i p_ilog(p_i)\\ p_j=1-\sum_i p_i,i\ne j\\ \dfrac{\partial H}{\partial p_i}=-[1+log(p_i)-1-log(p_j)]\\ =-log(\dfrac{p_i}{1-p_i-\sum_k^{k\ne i,j }p_k}) 　　　　　　(1)\\ \dfrac{\partial ^2 H}{\partial p_i^2}=-\dfrac{1}{p_i}-\dfrac{1}{1-p_i-\sum_k^{k\ne i,j }p_k}<0　　　　　(2)$$
(1)式是熵的一阶导数，(2)式是熵的二阶导，由于:

a . 二阶导小于零

b . $p_i=0$的时候一阶导$\to +\infty$，$p_i=1$的时候一阶导$\to -\infty$

得出则熵的函数是一个上凸的函数，函数的极值点就是最大值点。

对于每一个$i\ne j$ 都有式子$\dfrac{p_i}{1-p_i-\sum_k^{k\ne i,j }p_k}=1$,则有所有$p_i(i\ne j)$相等，记为p，则有

$$\dfrac{p}{1-(n-1)p}=1\\ p=\dfrac{1}{n}$$
即当且仅当随机变量所有的事件的概率相等时，随机变量的熵值取得最大值。

1.3 凸函数性质

注意：这里的凸函数是指的下凸，上凸称作凹

凸函数$f(x)$有两个性质

1. 二阶导大于零
2. 对所有$0<=\lambda<=1 x_1\ne x_2$，有$f(\lambda x_1+(1-\lambda)x_2)<=\lambda f(x_1)+(1-\lambda)f(x_2)$

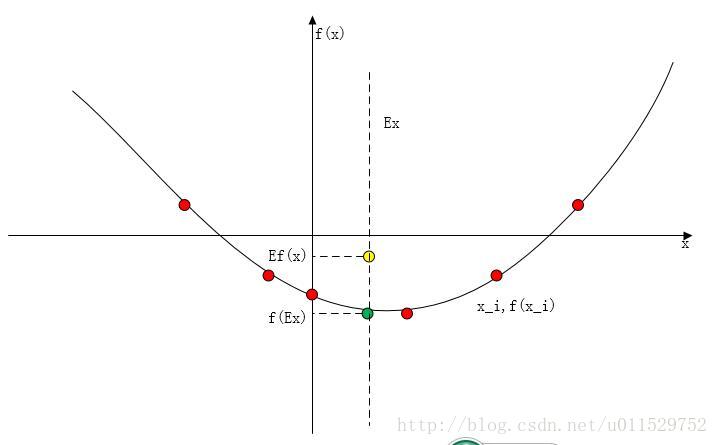
Jensen不等式：

对于一个下凸的函数f和一个随机变量X，有

$$Ef(X)>=f(EX)$$
证明：

考虑离散情况，使用数学归纳法：

当只有二项分布的时候，由凸函数的性质，有$p_1f(x_1)+p_2f(x_2)>=f(p_1x_1+p_2x_2)$，显然成立。

假设有n-1个分布点的时候，不等式成立，即已知

$$\sum_{i=1}^{n-1}p_if(x_i)>=f(\sum_{i=1}^{k-1}p_ix_i)$$
对于n个分布点：
$$\sum_{i=1}^np_if(x_i)=p_nf(x_n)+\sum_{i=1}^{n-1}p_if(x_i)\\ =p_nf(x_n)+(1-p_n)\sum_{i=1}^{n-1}\frac{p_i}{1-p_n}f(x_i)\\ >=p_nf(x_n)+(1-p_n)f(\sum_{i=1}^{n-1}\frac{p_i}{1-p_n}x_i)\\ >=f(p_nx_n+(1-p_n)\sum_{i=1}^{n-1}\frac{p_i}{1-p_n}x_i)\\ =f(\sum_{i=1}^{n}p_ix_i)$$
即得证。

形象地：

红点是随机分布的分布点，绿点是$f(Ex)$,黄点所在的纵坐标是$E(f(x))$,显然有$f(E(x))<=E(f(x))$ 的

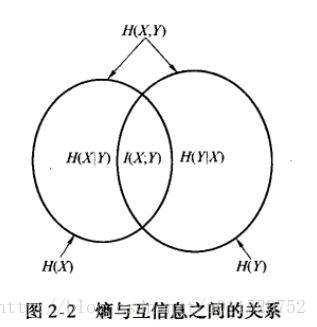
2. 联合熵与条件熵

2.1 联合熵

对于二元的概率，联合熵为

$$H(X,Y)=-\sum p(x,y)log(p(x,y))\\ =E(I(x,y))$$

2.2 条件熵

当X取某一观测值，条件概率为$p(Y|X=x)$,此时对于随机变量Y来说，在X=x的条件下熵是：

$$H(Y|X=x)=-\sum p(y|x)log(p(y|x))$$
条件熵就定义为当X取遍所有观测值时，随机变量Y的熵的期望
$$H(Y|X)=\sum p(x)H(Y|X=x)\\ =-\sum_x p(x)\sum_y p(y|x)log(p(y|x))\\ =-\sum_x \sum_y p(x,y)log(p(y|x))$$
链式法则：
$$H(X,Y)=-\sum_x \sum_y p(x,y)log(p(x,y))\\ =-\sum_x \sum_y p(x,y)log(p(y|x)p(x))\\ =-\sum_x \sum_y p(x,y)log(p(y|x))-\sum_x \sum_y p(x,y)log(p(x))\\ =H(Y|X)-\sum_x \sum_y p(x,y)log(p(x))\\ =H(Y|X)-\sum_xp(x)log(x)\\ =H(Y|X)+H(X)$$
也可以由
$$-log(p(x,y))=-log(p(y|x))-log(x)$$
两边同时取期望得到

2.3 联合熵和条件熵的辨析

​ 条件熵是在确定某一条件的情况下，系统的平均不确定度。此时如果加上自身的不确定度，则等于系统的整体不确定度。即条件确定，条件下的状态确定，则系统确定。

3. 相对熵与互信息

3.1 相对熵

假设有一个随机变量X，对于他所有的取值x，都对应着两个分布p和q，即

$$\begin{vmatrix} X \\ p \\ q \end{vmatrix}\begin{vmatrix} x_0 & x_1&... &x_{n-1} \\ p_0 & p_1&... &p_{n-1}\\ q_0 & q_1&... &q_{n-1}\\ \end{vmatrix}$$
假设相对熵描述对于相同取值的随机变量的不同分布之间的距离
$$D(p||q)=\sum_i p_ilog(\dfrac{p_i}{q_i})$$
辨析：

a. 距离是相对的而且是不对称的，$D(p||q)\ne D(q||p)$,在度量的时候要么在$D(p||q)$的框架下，要么反之，不能混用。

b.$D(p||q)>=0$,当且仅当所有$p_i=q_i$的时候取等号。

证明：

$$-D(p||q)=-\sum_ip_ilog(\dfrac{p_i}{q_i})\\ =\sum_ip_ilog(\dfrac{q_i}{p_i})\\ <=log(\sum_ip_i\dfrac{q_i}{p_i})\\ =log(sum_i p_i)=log(1)=0$$
得 $D(p||q)>=0$,只有当所有 $p_i=cq_i$，的时候取等号，又 $\sum_ip_i=\sum_iq_i=1$,有 $\sum_ip_i=c\sum_iq_i=\sum_iq_i$,得c=1 。即只有当所有 $p_i=q_i$的时候，才能取等号。

c.约定$0log\dfrac{0}{0}=0$,$0log(\dfrac{0}{q})=0$,$plog(\dfrac{p}{0})=\infty$

3.2 互信息

互信息用来描述两个随机变量之间的相关性，定义为联合概率密度和概率密度之积 的相对熵。

$$I(X;Y)=\sum_x\sum_yp(x,y)log(\dfrac{p(x,y)}{p(x)p(y)})\\ =D(p(x,y)||p(x)p(y))$$
辨析：

a. 当I(X;Y)值比较大的时候，表明相关性很强，因为p(x)p(y)表示如果两个随机变量独立分布的时候的概率密度。反之，如果I(X;Y)的值很小甚至接近于0，表明X和Y的相关性很弱，因为联合概率密度接近于独立分布的概率密度。

b.互信息是对称的，I(X;Y)=I(Y;X)，只是分母分子不能反。

c.互信息的链式规则：

$$I(X;Y)=\sum_x\sum_yp(x,y)log(\dfrac{p(x,y)}{p(x)p(y)})\\ =\sum_{x,y}p(x,y)log(\dfrac{p(x|y)}{p(x)})\\ =-\sum_x p(x)log(p(x))-(-\sum_{x,y}p(x,y)log(p(x|y)))\\ =H(X)-H(X|Y)=H(Y)-H(Y|X)$$
互信息也可以解释为给定Y的情况下X的不确定程度的减少量，如果给定Y，X的熵并没有变少，则X和Y相对独立，减少量就少。反之，给定Y后熵的减少量多，则X和Y之间存在很强的相关性。

3.3 自信息

现有的链式法则有：

$$H(X,Y)=H(X)+H(Y|X)=H(Y)+H(X|Y)\\ I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)$$
得
$$I(X;Y)=H(X)+H(Y)-H(X,Y)$$
自信息
$$I(X;X)=H(X)+H(X)-H(X,X)=H(X)$$