C++ 朴素贝叶斯模型（Naive Bayesian Model，NBM）实现， 西瓜实验数据集 基于周志华老师机器学习

最新推荐文章于 2024-08-28 06:28:25 发布
最新推荐文章于 2024-08-28 06:28:25 发布
阅读量5.5k 收藏 18
点赞数 7
分类专栏： 大数据算法 文章标签： C++ 统计学习 朴素贝叶斯 C++实现 x
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/u011557212/article/details/52786108
版权

C++ 朴素贝叶斯模型（Naive Bayesian Model，NBM）实现， 西瓜实验数据集 基于周志华老师机器学习

版权声明：本文为博主原创文章，未经博主允许不得转载。

标注

学习朴素贝叶斯算法得了解一些基本知识，比如全概率公式和贝叶斯公式。大学基本都学过不在赘述。

数据样本

编号色泽根蒂敲声纹理脐部触感密度含糖率好瓜
12221310.6970.461
23231310.7440.3761
33221310.6340.2641
42231310.6080.3181
51221310.5560.2151
62121220.4030.2371
73122220.4810.1491
83121210.4370.2111
93132210.6660.0910
102311120.2430.2670
111313110.2450.0570
121223120.3430.0990
132122310.6390.1610
141132310.6570.1980
153121220.360.370
161223110.5930.0420
172232210.7190.1030

表格含义

色泽 1-3代表 浅白 青绿 乌黑
根蒂 1-3代表 稍蜷 蜷缩 硬挺
敲声 1-3代表 清脆 浊响 沉闷
纹理 1-3代表 清晰 稍糊 模糊
脐部 1-3代表 平坦 稍凹 凹陷
好瓜 1代表 是 0 代表 不是

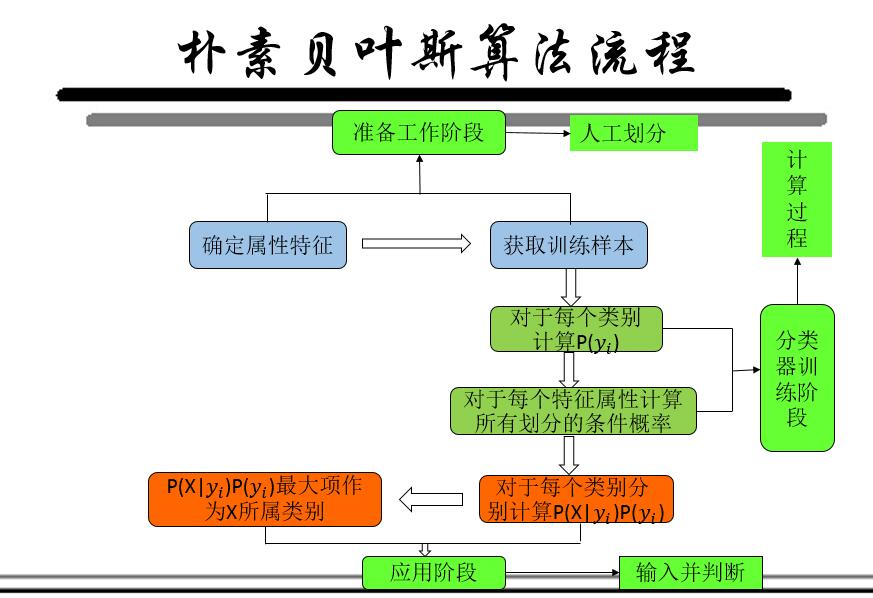
算法定义

朴素贝叶斯算法定义如下：
这里写图片描述
这里写图片描述

代码块

//bayesian.h
#pragma once
//定义训练数据  
#define M 17  
#define N 9  
/*
*色泽 1—3代表 浅白 青绿 乌黑
*根蒂 1-3代表 稍蜷 蜷缩 硬挺
*敲声1-3代表 清脆 浊响 沉闷
*纹理 1-3代表 清晰 稍糊 模糊         
*脐部1-3代表 平坦 稍凹 凹陷          
*触感 1-2 代表 硬滑 软粘            
*好瓜 1代表是 0 代表不是                             
*/  
double A[M][N]= {  
    {2,2,2,1,3,1,0.697,0.460,1},//  1
    {3,2,3,1,3,1,0.744,0.376,1},//  2
    {3,2,2,1,3,1,0.634,0.264,1},//  3
    {2,2,3,1,3,1,0.608,0.318,1},//  4
    {1,2,2,1,3,1,0.556,0.215,1},//  5
    {2,1,2,1,2,2,0.403,0.237,1},//  6
    {3,1,2,2,2,2,0.481,0.149,1},//  7
    {3,1,2,1,2,1,0.437,0.211,1},//  8
    {3,1,3,2,2,1,0.666,0.091,0},//  9
    {2,3,1,1,1,2,0.243,0.267,0},//  10
    {1,3,1,3,1,1,0.245,0.057,0},//  11
    {1,2,2,3,1,2,0.343,0.099,0},//  12
    {2,1,2,2,3,1,0.639,0.161,0},//  13
    {1,1,3,2,3,1,0.657,0.198,0},//  14
    {3,1,2,1,2,2,0.360,0.370,0},//  15
    {1,2,2,3,1,1,0.593,0.042,0},//  16
    {2,2,3,2,2,1,0.719,0.103,0} //  17

};  

struct Px1  
{  
    double x1;  
    double y;  
    double p_x1y;  
};  

struct Px2  
{  
    double x2;  
    double y;  
    double p_x2y;  
};  

struct Px3  
{  
    double x3;  
    double y;  
    double p_x3y;  
};  
struct Px4  
{  
    double x4;  
    double y;  
    double p_x4y;  
};  
struct Px5  
{  
    double x5;  
    double y;  
    double p_x5y;  
};  
struct Px6  
{  
    double x6;  
    double y;  
    double p_x6y;  
};  
struct Px7  
{  
    double x7;  
    double y;  
    double p_x7y;  
};  
struct Px8  
{  
    double x8;  
    double y;  
    double p_x8y;  
};  
// struct MeAVa 
// {  
//  double mean;  
//  double stdev;  
// };  

double p[2];  
Px1 px1[6];  
Px2 px2[6];
Px3 px3[6];
Px4 px4[6];
Px5 px5[6];
Px6 px6[6];
Px7 px7[2];
Px8 px8[2];  

//bayesian .cpp
#include "bayesian.h"
#include <iostream>  
#include <set>  
#include <vector>  
#include <numeric>
#include <algorithm>
#include <iomanip>
//#include <math.h>
#include <cmath>
using namespace std;  
//好瓜密度概率计算
double m_MeansAndAver(double x)
{

    double resultSet[17];
    double p;
    for (int i = 0; i < M; i++)
    {
        resultSet[i]=A[i][6];
    }
    double sum = std::accumulate(std::begin(resultSet), std::begin(resultSet)+8, 0.0);
    double mean=  sum /8; //均值
    double accum  = 0.0;
    std::for_each (std::begin(resultSet), std::begin(resultSet)+8, [&](const double d) {
        accum  += (d-mean)*(d-mean);
    });

    double stdev = sqrt(accum/(7)); //方差
//  std::cout<<"--------------------test1-------------------------------"<<stdev<<endl;
//  std::cout<<"均值为"<<mean<<"方差为："<<stdev<<endl;
//  std::cout<<"--------------test---------------"<<endl;
    p = (1/(sqrt(2*3.14)*stdev))*exp(-(pow((x-mean),2)/(2*pow(stdev,2))));
    //px7[0]=p;
    px7[0].p_x7y=p ;
    return p;
}
//坏瓜密度概率计算
double m_w_MeansAndAver(double x)
{

    double resultSet[17];
    double p;
    for (int i = 0; i < M; i++)
    {
        resultSet[i]=A[i][6];
    }
    double sum = std::accumulate(std::begin(resultSet)+8, std::end(resultSet), 0.0);
    double mean=  sum /9; //均值
    double accum  = 0.0;
    std::for_each ( std::begin(resultSet)+8,std::end(resultSet), [&](const double d) {
        accum  += (d-mean)*(d-mean);
    });

    double stdev = sqrt(accum/(8)); //方差
//  std::cout<<"--------------------test2-------------------------------"<<stdev<<endl;
//  std::cout<<"均值为"<<mean<<"方差为："<<stdev<<endl;
//  std::cout<<"--------------test---------------"<<endl;
    p = (1/(sqrt(2*3.14)*stdev))*exp(-(pow((x-mean),2)/(2*pow(stdev,2))));
    px7[1].p_x7y=p ;
    return p;
}
//好瓜含糖量概率计算
double h_MeansAndAver(double x)
{

    double resultSet[17];
    double p;
    for (int i = 0; i < M; i++)
    {
        resultSet[i]=A[i][7];
    }
    double sum = std::accumulate(std::begin(resultSet), std::begin(resultSet)+8, 0.0);
    double mean=  sum /8; //均值
    double accum  = 0.0;
    std::for_each (std::begin(resultSet), std::begin(resultSet)+8, [&](const double d) {
        accum  += (d-mean)*(d-mean);
    });

    double stdev = sqrt(accum/(7)); //方差
//  std::cout<<"--------------------test3--------------------------------"<<stdev<<endl;
//  std::cout<<"均值为"<<mean<<"方差为："<<stdev<<endl;
//  std::cout<<"--------------test---------------"<<endl;
    p = (1/(sqrt(2*3.14)*stdev))*exp(-(pow((x-mean),2)/(2*pow(stdev,2))));
    px8[0].p_x8y=p;
    return p;
}

//坏瓜含糖量概率计算
double h_w_MeansAndAver(double x)
{

    double resultSet[17];
    double p;
    for (int i = 0; i < M; i++)
    {
        resultSet[i]=A[i][7];
    }
    double sum = std::accumulate(std::begin(resultSet)+8, std::end(resultSet), 0.0);
    double mean=  sum /9; //均值
    double accum  = 0.0;
    std::for_each (std::begin(resultSet)+8,  std::end(resultSet), [&](const double d) {
        accum  += (d-mean)*(d-mean);
    });

    double stdev = sqrt(accum/(8)); //方差
//  std::cout<<"--------------------test4--------------------------------"<<stdev<<endl;
//  std::cout<<"均值为"<<mean<<"方差为："<<stdev<<endl;
//  std::cout<<"--------------test---------------"<<endl;
    p = (1/(sqrt(2*3.14)*stdev))*exp(-(pow((x-mean),2)/(2*pow(stdev,2))));
    px8[1].p_x8y=p;
    return p;
}
//计算先验概率和条件概率  
void calP()  
{
    //计算先验  
    //double p[2];  
    int i, j, k;  
    multiset<double> m_x1, m_x2,m_x3, m_x4,m_x5, m_x6,m_x7, m_x8, m_y;//多重集容器  
    multiset<double>::iterator pos1;  

    set<double> x1, x2,x3, x4,x5, x6,x7, x8, y;//集合容器  
    set<double>::iterator pos2, pos3;  

    //运用多重集容器和集合容器  
    for(i = 0; i < M; i++) 
    {
        m_x1.insert(A[i][0]);  
        m_x2.insert(A[i][1]);
        m_x3.insert(A[i][2]);
        m_x4.insert(A[i][3]);
        m_x5.insert(A[i][4]);
        m_x6.insert(A[i][5]);
        m_x7.insert(A[i][6]);
        m_x8.insert(A[i][7]);
        m_y.insert(A[i][8]);  

        x1.insert(A[i][0]);  
        x2.insert(A[i][1]);
        x3.insert(A[i][2]);
        x4.insert(A[i][3]);
        x5.insert(A[i][4]);
        x6.insert(A[i][5]);
        x7.insert(A[i][6]);
        x8.insert(A[i][7]);
        y.insert(A[i][8]); 

    }  


    p[0] = m_y.count(1) / (double)M;    //p(Y = 1)  
    p[1] = m_y.count(0) / (double)M;    //p(Y = 2)  
    cout << endl << "************先验***********" << endl; 
//p[0]代表好瓜所占的比例  p[1]代表坏瓜所占的比例
    cout << "p(Y = 1) = " << p[0] << endl;  
    cout << "p(Y = 0) = " << p[1] << endl; 

//计算条件概率  
    cout << endl;  
    cout << "*********条件概率********" << endl;  
    //  int px1_num = 3 * 2;  
    //  int px2_num = 3 * 2;  
//p(x1 | y)概率
    j=0; 
    for(pos2 = y.begin(); pos2 != y.end(); pos2++)  
    { 
        for(pos3 = x1.begin(); pos3 != x1.end(); pos3++)  
        {       
            px1[j].y = *pos2;  
            px1[j].x1 = *pos3;  

            int count_x1y = 0;  
            for(k = 0; k < M; k++)  
            {  
                if(A[k][0] == px1[j].x1 && A[k][8] == px1[j].y)  
                    count_x1y++;  
            }  
            px1[j].p_x1y = count_x1y / (double)m_y.count(px1[j].y);//计算p(x1 | y)的概率  
            j++;  
        }  
    }  

    cout << "p(x1 | y):" << endl;  
    for(j = 0; j < 6; j++)  
    {  
        cout << px1[j].x1 << " " <<  px1[j].y << " " << px1[j].p_x1y << endl;  
    }  
//p(x2|y)概率
    j=0;  
    for(pos2 = y.begin(); pos2 != y.end(); pos2++)  
    {  
        for(pos3 = x2.begin(); pos3 != x2.end(); pos3++)  
        {  
            px2[j].y = *pos2;  
            px2[j].x2 = *pos3;  

            int count_x2y = 0;  
            for(k = 0; k < M; k++)  
            {  
                if(A[k][1] == px2[j].x2 && A[k][8] == px2[j].y)  
                    count_x2y++;  
            }  
            px2[j].p_x2y = count_x2y / (double)m_y.count(px2[j].y);//计算p(x2 | y)的概率  
            j++;  
        }  
    }  

    cout << "p(x2 | y):" << endl;  
    for(j = 0; j < 6; j++)  
    {  
        cout << px2[j].x2 << " " <<  px2[j].y << " " << px2[j].p_x2y << endl;  
    }  


//p(x3|y)概率
    j=0;  
    for(pos2 = y.begin(); pos2 != y.end(); pos2++)  
    {  
        for(pos3 = x3.begin(); pos3 != x3.end(); pos3++)  
        {  
            px3[j].y = *pos2;  
            px3[j].x3 = *pos3;  

            int count_x3y = 0;  
            for(k = 0; k < M; k++)  
            {  
                if(A[k][2] == px3[j].x3 && A[k][8] == px3[j].y)  
                    count_x3y++;  
            }  
            px3[j].p_x3y = count_x3y / (double)m_y.count(px3[j].y);//计算p(x2 | y)的概率  
            j++;  
        }  
    }  

    cout << "p(x3 | y):" << endl;  
    for(j = 0; j < 6; j++)  
    {  
        cout << px3[j].x3 << " " <<  px3[j].y << " " << px3[j].p_x3y << endl;  
    }  
//p(x4|y)概率
    j=0;  
    for(pos2 = y.begin(); pos2 != y.end(); pos2++)  
    {  
        for(pos3 = x4.begin(); pos3 != x4.end(); pos3++)  
        {  
            px4[j].y = *pos2;  
            px4[j].x4 = *pos3;  

            int count_x4y = 0;  
            for(k = 0; k < M; k++)  
            {  
                if(A[k][3] == px4[j].x4 && A[k][8] == px4[j].y)  
                    count_x4y++;  
            }  
            px4[j].p_x4y = count_x4y / (double)m_y.count(px4[j].y);//计算p(x4 | y)的概率  
            j++;  
        }  
    }  

    cout << "p(x4 | y):" << endl;  
    for(j = 0; j < 6; j++)  
    {  
        cout << px4[j].x4 << " " <<  px4[j].y << " " << px4[j].p_x4y << endl;  
    }  
//p(x5|y)概率
    j=0;  
    for(pos2 = y.begin(); pos2 != y.end(); pos2++)  
    {  
        for(pos3 = x5.begin(); pos3 != x5.end(); pos3++)  
        {  
            px5[j].y = *pos2;  
            px5[j].x5 = *pos3;  

            int count_x5y = 0;  
            for(k = 0; k < M; k++)  
            {  
                if(A[k][4] == px5[j].x5 && A[k][8] == px5[j].y)  
                    count_x5y++;  
            }  
            px5[j].p_x5y = count_x5y / (double)m_y.count(px5[j].y);//计算p(x5 | y)的概率  
            j++;  
        }  
    }  

    cout << "p(x5 | y):" << endl;  
    for(j = 0; j < 6; j++)  
    {  
        cout << px5[j].x5 << " " <<  px5[j].y << " " << px5[j].p_x5y << endl;  
    }  
//p(x6|y)概率
    j=0;  
    for(pos2 = y.begin(); pos2 != y.end(); pos2++)  
    {  
        for(pos3 = x6.begin(); pos3 != x6.end(); pos3++)  
        {  
            px6[j].y = *pos2;  
            px6[j].x6 = *pos3;  

            int count_x6y = 0;  
            for(k = 0; k < M; k++)  
            {  
                if(A[k][5] == px6[j].x6 && A[k][8] == px6[j].y)  
                    count_x6y++;  
            }  
            px6[j].p_x6y = count_x6y / (double)m_y.count(px6[j].y);//计算p(x6 | y)的概率  
            j++;  
        }  
    }  

    cout << "p(x6 | y):" << endl;  
    for(j = 0; j < 6; j++)  
    {  
        cout << px6[j].x6 << " " <<  px6[j].y << " " << px6[j].p_x6y << endl;  
    }  
//p(x7|y)概率

} 
int main()  
{  
    int i = 0, j = 0;  
    //输出训练数据  
    cout << "***********训练数据************" << endl;  
    for(i = 0; i < M; i++)  
    {  
        for(int j = 0; j < N; j++)  
        {  
            cout << " "<< A[i][j];  
        }  
        cout << endl;  
    } 

    calP();//计算先验和条件概率  
    int s_x1, s_x2, s_x3, s_x4, s_x5, s_x6;
    double  s_x7, s_x8;  
    double result[2];  
    int class_y = 1;  
    cout<< "##########################< 提   示 >##########################"<<endl;
    cout<<setw(10)<<"色泽"<<setw(10)<<"1-3代表"<<setw(10)<<"浅白"<<setw(10)<<"青绿"<<setw(10)<<"乌黑"<<endl;
    cout<<setw(10)<<"根蒂"<<setw(10)<<"1-3代表"<<setw(10)<<"稍蜷"<<setw(10)<<"蜷缩"<<setw(10)<<"硬挺"<<endl;
    cout<<setw(10)<<"敲声"<<setw(10)<<"1-3代表"<<setw(10)<<"清脆"<<setw(10)<<"浊响"<<setw(10)<<"沉闷"<<endl;
    cout<<setw(10)<<"纹理"<<setw(10)<<"1-3代表"<<setw(10)<<"清晰"<<setw(10)<<"稍糊"<<setw(10)<<"模糊"<<endl;
    cout<<setw(10)<<"脐部"<<setw(10)<<"1-3代表"<<setw(10)<<"平坦"<<setw(10)<<"稍凹"<<setw(10)<<"凹陷"<<endl;
    cout<<setw(10)<<"触感"<<setw(10)<<"1-2代表"<<setw(10)<<"硬滑"<<setw(10)<<"软粘"<<endl;
    cout<<"      密度以及含糖量 0<Xi<1 "<<endl;
    cout<<"      请按照以上范围输入"<<endl;
    cout<< "###############################################################"<<endl;
    /************************************************************************/
    /* 
    色泽  1-3代表  浅白  青绿  乌黑
    根蒂  1-3代表  稍蜷  蜷缩  硬挺
    敲声  1-3代表  清脆  浊响  沉闷
    纹理  1-3代表  清晰  稍糊  模糊
    脐部  1-3代表  平坦  稍凹  凹陷
    触感  1-2代表  硬滑  软粘    
    好瓜  1代表 是  0 代表  不是                             
    */
    /************************************************************************/

    cout <<endl<< "##########################< 预   测 >##########################"<<endl; 
    cout <<endl<<"Input:";  
    cin >> s_x1 >> s_x2>> s_x3>> s_x4>> s_x5>> s_x6>> s_x7>> s_x8; 
    cout << "##########<连续属性X7与x8的 p(x7|y)、<p(x8|y)计算结果>##########"<<endl<<endl; 
    cout<<"好瓜密度其概率为："<<m_MeansAndAver(s_x7)<<endl;//当前密度，在是好瓜的情况下可能发生的概率
    cout<<"坏瓜密度的概率"<<m_w_MeansAndAver(s_x7)<<endl;//准确
    cout<<"好瓜其概率为："<<h_MeansAndAver(s_x8)<<endl;//准确
    cout<<"好瓜其概率为："<<h_w_MeansAndAver(s_x8)<<endl<<endl;//准确

    for(i = 0; i < 2; i++)  
    {  
        double s_px_1, s_px_2, s_px_3, s_px_4, s_px_5, s_px_6, s_px_7, s_px_8;  
        for(j = 0; j < 6; j++)  
        {  
            if(s_x1 == px1[j].x1 && px1[j].y == class_y)  
                s_px_1 = px1[j].p_x1y;  
            if(s_x2 == px2[j].x2 && px2[j].y == class_y)
                s_px_2 = px2[j].p_x2y;  
            if(s_x3 == px3[j].x3 && px3[j].y == class_y)
                s_px_3 = px3[j].p_x3y;  
            if(s_x4 == px4[j].x4 && px4[j].y == class_y)
                s_px_4 = px4[j].p_x4y;  
            if(s_x5 == px5[j].x5 && px5[j].y == class_y)
                s_px_5 = px5[j].p_x5y;  
            if(s_x6 == px6[j].x6 && px6[j].y == class_y)
                s_px_6 = px6[j].p_x6y;  
        }  
        s_px_7=px7[i].p_x7y;
        s_px_8=px8[i].p_x8y;
        result[i] = p[i] * s_px_1 * s_px_2*s_px_3* s_px_4* s_px_5* s_px_6*s_px_7*s_px_8;  //p[0]代表好瓜所占的比例  p[1]代表坏瓜所占的比例
        class_y--;  
    }  
    cout << "###########################<分类结果>###########################"<<endl; 
    cout << endl << "all results:";  
    cout <<"可能为好瓜的概率"<< result[0] << "   " <<"可能为坏瓜的概率"<< result[1] << endl<<endl;  //0代表否（不是好瓜），1代表是好瓜，其中result[0]存放好瓜可能概率result[1]坏瓜所占比例
    cout << "###########################<预测结果>###########################"<<endl<<endl;  
    i =0;
    if(result[i] < result[i+1])  //如果坏瓜概率>好瓜概率
        {  
            class_y = 0; 
            cout << "属性为：("<< s_x1 << "," << s_x2 << "," << s_x3 << "," << s_x4 << "," 
                << s_x5 << "," << s_x6<< "," << s_x7<< "," << s_x8 << ")所属的类是：" << class_y<< "-----------坏瓜"<<endl<<endl;  
        }  
    else                        //好瓜概率>坏瓜概率
    {
        class_y=1;
        cout << "属性为：("<< s_x1 << "," << s_x2 << "," << s_x3 << "," << s_x4 << "," 
            << s_x5 << "," << s_x6 << "," << s_x7<< "," << s_x8 << ")所属的类是：" << class_y  <<"-----------好瓜"<< endl<<endl;  
    }
    /*cout << "("<< s_x1 << "," << s_x2 << ")所属的类是：" << class_y + 1 << endl;  */
    system("pause");
    return 0;  
}

“`

分类结果

这里写图片描述

UML 图:

这里写图片描述

源码下载地址

http://download.csdn.net/detail/u011557212/9700532

Elijah_Yi
关注
专栏目录
朴素贝叶斯西瓜数据集
12-01
朴素贝叶斯相关西瓜数据集，用于自然语言处理>01.朴素贝叶斯介绍 中的案例数据，该数据集仅作参考使用
Kaggle 机器学习实战 朴素贝叶斯（原理+西瓜数据集实战）
weixin_43462804的博客
09-16 2600
类别先验概率的估计，即某一类的数量占总体数量的比例 P(c)=DcD P(c)=\frac{D_c}{D} P(c)=DDc​​ 类别概率密度估计，即类条件概率，分两种情况​ xix_ixi​离散情况：Dc,xiD_{c,x_i}Dc,xi​​表示DcD_cDc​在第iii个属性上取值为xix_ixi​的样本组成的集合 P(xi∣c)=Dc,xiDc P(x_i|c)=\frac{D_{c,x_i}}{D_c} P(xi​∣c)=Dc​Dc,xi​​​ ​ xix_ixi​连续情况：由某一概率密度估计
C++语言实现朴素贝叶斯算法
zy0412326的专栏
08-28 228
该实现适用于简单的文本分类问题。对于更复杂的数据，可以使用不同的数据结构和方法来处理特征工程、平滑处理等。
机器学习—朴素贝叶斯代码实现—西瓜书3.0
everybody hates me的博客
10-02 3041
代码实现西瓜分类，我们先上数据： 我的编程实现过程非常杂糅，没有系统，而且我的python也没学多久，所以用的都是简单的循环、函数。在编程过程中，我把色泽变量记为x1，根蒂记为x2，敲声记为x3，纹理记为x4，脐部记为x5，触感记为x6，密度记为x7，含糖率记为x8，是否为好瓜这一名义变量记好瓜为0，坏瓜为1。 接下来，我们引入一些有关朴素贝叶斯算法的基础知识： 首先是计算先验概率： 在实际编程过程中我直接使用拉普拉斯平滑，取λ=1\lambda=1λ=1 则先验概率为 Pλ(Y=ck)=∑i=1NI(y
朴素贝叶斯（西瓜数据集分类，社区恶意留言分类，垃圾邮件分类，新浪新闻分类），AODE分类器 代码实现
热门推荐
学海无涯的博客
06-24 1万+
朴素贝叶斯（社区恶意留言分类，垃圾邮件分类，新浪新闻分类）代码实现 以下代码为本人学习后，修改或补充后的代码实现，数据集和原代码请参考：https://github.com/Jack-Cherish/Machine-Learning 社区恶意留言分类 import numpy as np def loadDataSet(): # 创建实验样本 postingLis
统计学习方法（李航）算法4.1（朴素贝叶斯算法）C++简单实现
09-29
对《统计学习方法》（李航），算法4.1朴素贝叶斯算法，以例4.1为例用C++简单实现。
MATLAB 中实现朴素贝叶斯（Naive Bayesian）多特征分类预测的详细示例（包含详细的完整的程序和数据）
最新发布
10-03
本文提供了一个关于如何使用 MATLAB 在没有外部工具箱的情况下实现一个朴素贝叶斯分类预测模型的具体步骤和实例源代码。主要讲解数据准备方法, 包括模拟的数据创建；介绍了模型的设计思想以及实现步骤；演示了基于...
基于传统机器学习(朴素贝叶斯 逻辑斯蒂回归 lightGBM)实现中文文本分类python源码+文本数据集+项目说明.zip
05-15
基于传统机器学习(朴素贝叶斯 逻辑斯蒂回归 lightGBM)实现中文文本分类python源码+文本数据集+项目说明.zip 【项目介绍】 中文文本分类 传统机器学习 目录及文件说明 bert_pretrain存放bert预训练的参数及模型 ...
机器学习及与智能数据处理Python使用朴素贝叶斯算法对垃圾短信数据集进行分类中的垃圾短信数据集
05-29
机器学习及与智能数据处理Python使用朴素贝叶斯算法对垃圾短信数据集进行分类中的垃圾短信数据集。 朴素贝叶斯算法 输入：样本集合D=｛(x_1,y_1),(x_2,y_2)~(x_m,y_m); 待预测样本x; 样本标记的所有可能取值｛c_1,c_...
用python朴素贝叶斯实现垃圾邮件分类的数据集
11-06
使用机器学习算法 用python朴素贝叶斯实现垃圾邮件分类的数据集
基于朴素贝叶斯机器学习算法实现情感文本分析与分类源码+数据集（高分大作业）.zip
08-16
基于朴素贝叶斯机器学习算法实现情感文本分析与分类源码+数据集（高分大作业）.zip 该项目是个人大作业项目源码，评审分达到95分以上，都经过严格调试，确保可以运行！放心下载使用。 该项目资源主要针对计算机相关...
机器学习西瓜分类贝叶斯算法实例详解
10-17
机器学习-贝叶斯-西瓜分类 对代码的每一行进行了注解，适合初学者使用，主要代码来源是百度ai社区，只是对其进行了注解
C++实现朴素贝叶斯分类器(加强版)
09-14
这个和我以前传的有了一点改动就是把训练模型和预测分为了2个工程了更方便了 里面有readme.txt. 还可以看看我前面上传那个工程的“资源描述”
贝叶斯分类数据集
03-28
贝叶斯数据集，参考matlab：https://blog.csdn.net/qq_38784454/article/details/79729941
编程实现贝叶斯分类
weixin_33717117的博客
12-19 200
前言，目前正在做一项搜索引擎相关的大作业，用到贝叶斯分类。想到的方法首先是学习网友的。 见：http://www.cnblogs.com/phinecos/archive/2008/10/21/1316044.html 目标：看懂其用java写的程序，领会算法，然后转成c#版本的。（因为分类只是我项目中的一个功能，我整个框架都是用C#搭建的，所以自然要换成C#）也顺便学学学java.java还...
统计学习笔记：朴素贝叶斯（Naive Bayes）原理及C++源码实现
Morris的博客
05-01 2881
朴素贝叶斯（用于分类）一、概念朴素贝叶斯法是在假设输入向量x的特征条件独立（即在输入模式所属类别确定时，输入向量x的每个元素取值互不影响）下，通过样本集合学习输入x与输出y的联合概率分布。再用所得到的联合概率分布通过贝叶斯公式计算条件概率（后验概率）。将输入模式分类到后验概率最大的一个类别中。二、方法2.1 贝叶斯公式假设需对n个类别进行分类，按照贝叶斯公式：式中ck表示输出y的类别，k=1,2,...
基于朴素贝叶斯分类器的西瓜数据集 2.0 预测分类_经典分类模型朴素贝叶斯解读...
weixin_39523529的博客
11-24 1201
贝叶斯分类器在早期的自然语言处理任务中有着较多实际的应用，例如大部分的垃圾邮件处理都是用的贝叶斯分类器。贝叶斯分类器的理论对于理解后续的NLP模型有很大的进益，感兴趣的小伙伴一定要好好看看，本文会详细的讲述贝叶斯分类器的原理。1 贝叶斯决策论贝叶斯决策论是在统计概率框架下进行分类决策的基本方法。对于分类任务来说，在 所有相关概率 都已知的情况下，贝叶斯决策论考虑如何基于这些概率和误判损失来预测分类...
朴素贝叶斯分类器简介及C++实现(性别分类)
网络资源是无限的
09-22 7421
朴素贝叶斯分类器简介及C++实现(性别分类)
西瓜书贝叶斯分类器（总结）
Farmer-Lei
03-23 1074
1.理论基础（可通过本小节的简单说法开始）##通过新进来样本的特征（特征）来估计该样本类别的概率就是后验概率，来最小化决策风险即由特征得属于哪一类别的概率，计算方法有两类：（1）通过判别式模型（如支持向量机，决策树等）直接对后验概率进行建模预测（略过）;（2）后验概率通过贝叶斯定理，将后验概率转换为基于训练集d估计先验概率和似然（即样本X相对于类标记的类条件概率，p（X | C）），简言之，通过给...
构建朴素贝叶斯垃圾邮件过滤器的机器学习训练集
资源摘要信息:"本资源包含了一个用于训练朴素贝叶斯垃圾邮件过滤器的数据集，该数据集涵盖了垃圾邮件和非垃圾邮件的样本。数据集中的样本都是以文本形式提供的，可以用于机器学习算法中朴素贝叶斯分类器的训练。朴素...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值