LogLog和HyperLogLog

前言

前一篇文章Cardinality Estimation介绍了计算UV的几种方法，HashSet、Bitmap、LPC和PC，这一篇接着介绍LogLog、HyperLogLog算法。

算法过程及实现

LogLog和HyperLogLog算法将一个数字由二进制表示，这个二进制数视为一次伯努利过程的结果，进而进行估算，整个过程如下

三个变量

• h：hash函数，处理输入参数得到hash value。
• b：hash value的最左b位。
• m：长度为m的集合，m=2^b。

算法过程

1. 初始化长度为m的集合M。
2. 输入参数v，使用hash函数处理，得到x。
3. 取x的二进制表示的最高b位，得到j。
4. x的二进制数去掉b位后，1首次出现的位置w。
5. M[j]设置为M[j]和w取大的。
6. 根据计算公式，计算估值。

上述过程不易于理解，可以参考下stream-lib的HyperLogLog实现，加强理解，此外，下面还有一个此过程的模拟器，更加直观。

LogLog&HyperLogLog

LogLog和HyperLogLog的过程是一致的，不同的是估算函数，HyperLogLog使用调和平均数代替了LogLog的几何平均数，能够有效减少空桶对于结果的影响，具体查看相关论文，估算函数如下
LogLog：

HyperLogLog：

HyperLogLog过程模拟器

有大佬开发了HyperLogLog过程模拟器，使得HyperLogLog算法过程非常直观，易于理解，如下所示，是一次输入为3,247,019的过程

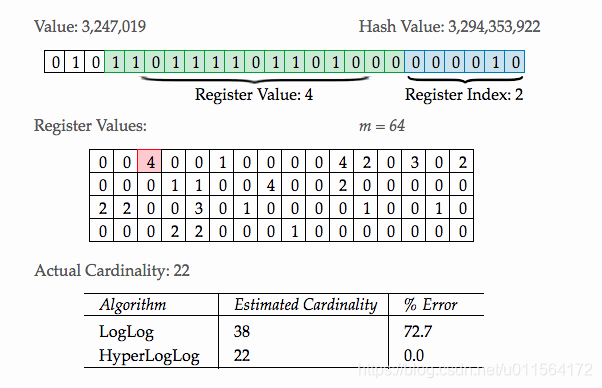
结合上面算法过程及实现中介绍的变量及过程，这里b=6，m=2^6=64，从上图可以得到算法过程如下

1. 输入为3,247,019，经过hash函数处理，得到x，3,294,353,922。
2. 取3,294,353,922的最低6位得到j，为2，如上图蓝色部分。
3. 去掉最低6位，剩余数字中1出现在右数第4位，得到w，等于4，如上图绿色部分。
4. 上图的Register Values为算法描述中的集合M，比较M[2]和w，设置M[2]为其中的大者，为4，如上图中粉红色部分。

应用

HyperLogLog因其估算精度高，节省内存，易于实现等特点，得到广泛应用，例如Redis HyperLogLog、Druid Cardinality aggregator、Approximate Algorithms in Apache Spark: HyperLogLog and Quantiles、Presto HyperLogLog Functions。

参考：
1.Loglog Counting of Large Cardinalities
2.HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm
3.stream-lib(HyperLogLog.java)
4.Sketch of the Day: HyperLogLog — Cornerstone of a Big Data Infrastructure