用数组存放树

最新推荐文章于 2024-07-24 11:55:42 发布

左林右李02

最新推荐文章于 2024-07-24 11:55:42 发布

阅读量2.9k

点赞数 2

分类专栏：数据结构

本文链接：https://blog.csdn.net/u011624157/article/details/115309322

版权

数据结构专栏收录该内容

11 篇文章

订阅专栏

本文介绍了满二叉树和完全二叉树的概念，重点讨论了链式存储法（链表结构）与基于数组的循序存储法（数组表示）。讲解了如何将链式结构转为数组（层次遍历）和数组转为链式（根据节点索引关系）。强调了完全二叉树的高效内存利用及其在堆和数据库中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

概念介绍

满二叉树和完全二叉树

在这里插入图片描述

上图中，编号 2 和编号 3 这两个二叉树是比较特殊的。

编号 2 的二叉树，叶子节点全在最底层，除了叶子节点之外，每个节点都有左右两个子节点，这种二叉树就叫作满二叉树。

编号 3 的二叉树中，叶子节点都在最底下两层，最后一层的叶子节点都靠左排列（最后一层的节点之间不能有空隙，从左到右不能有空隙），并且除了最后一层，其他层的节点个数都要达到最大，这种二叉树叫作完全二叉树。

存储树的两种方式

链式存储法

使用链表结构，每个节点有三个字段，数据、左节点指针、右节点指针。我们只要拎住根节点，就可以通过左右节点的指针，把整棵树都穿起来。这种存储方式比较常用，大部分二叉树代码都是通过这种结构来实现的。
在这里插入图片描述

基于数组的循序存储法

把根节点存储在下标 i = 1 的位置，把左子节点存储在下标 2 * i = 2 的位置，右子节点存储在 2 * i + 1 = 3 的位置。以此类推，B节点的左子节点存储在 2 * i = 2 * 2 = 4 的位置，右子节点存储在 2 * i + 1 = 2 * 2 + 1 = 5 的位置。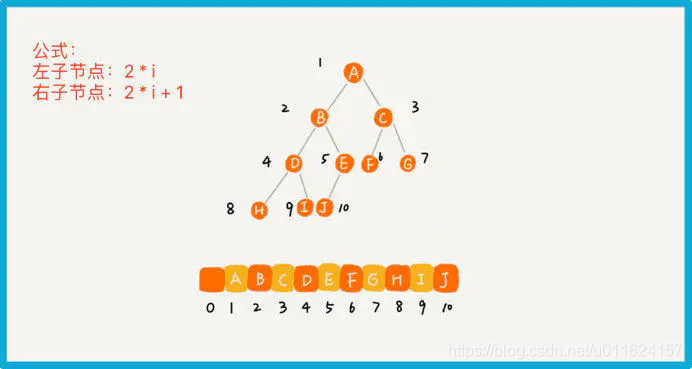
所以，求一个节点的父节点：floor(i/2) 即可（一般情况下，为了方便计算子节点，根节点都会存储在下标为 1 的位置）。

刚刚示例，其实就是一个完全二叉树，我们可以发现，完全二叉树会浪费下标为 0 的存储位置，如果是非完全二叉树的话，其实会浪费更多的数组存储空间。
在这里插入图片描述

所以，完全二叉树无疑是最节省内存的一种方式。因为数组的存储方式并不需要像链式存储法那样，要存储额外的左右子节点的指针。这也是为什么完全二叉树会单独拎出来的原因，也是为什么完全二叉树要求最后一层的子节点要从左到右排列的原因。

堆其实是一种完全二叉树，最常用的存储方式就是数组。

链表存储和数组存储互相转换

链式转数组（二叉树层次遍历）

思路：先将根节点入队，当前节点是队头节点，将其出队并访问，如果当前节点的左节点不为空将左节点入队，如果当前节点的右节点不为空将其入队。

代码如下

public void levelTraverse(TreeNode root) {
        Queue<TreeNode> q = new LinkedList<TreeNode>();
        if (root != null)
            q.offer(root);
        while (!q.isEmpty()) {
            TreeNode node = q.poll();
            System.out.println(node.value);
            if (node.leftNode != null)
                q.offer(node.leftNode);
            if (node.rightNode != null)
                q.offer(node.rightNode);
        }
}

数组转链式（根据节点在数组下标的关系）

在这里插入图片描述
根据上图描述，可得代码

注意：树的根结点对应数组下标为1

/**
     * 给定一个数组，构造出一颗完全二叉树
     *
     * @param arr
     */
    public TreeNode createTree(int[] arr) {
        ArrayList<TreeNode> treeNodeArrayList = new ArrayList<TreeNode>(20);
        treeNodeArrayList.add(null);
        for (int i = 0; i < arr.length; i++) {
            TreeNode node = new TreeNode(arr[i]);
            treeNodeArrayList.add(node);
        }
        for (int j = 1; j <= arr.length; j++) {
            if (2 * j <= arr.length)
                treeNodeArrayList.get(j).leftNode = treeNodeArrayList.get(2 * j);
            if ((2 * j + 1) <= arr.length)
                treeNodeArrayList.get(j).rightNode = treeNodeArrayList.get(2 * j + 1);
        }
        return treeNodeArrayList.get(1);
    }