美赛数模论文之表的格式

表的格式：表头在上 注：红字标记代表可通用的句子

1. 在表前对表的来源和数据进行说明
2. In Table 1, we summarize the minimum number of escorts needed to reach each service level

表的解释部分

For each airport, the difference between the Good and Adequate service levels is roughly a factor of two, with slightly increasing returns to scale; with larger scales, the staff are spread more uniformly, so it is less likely that a job will crop up with nobody close enough to take it.

例2

表的解释部分

（前面的说出数据的来源，然后筛选出比较代表性的数据进行说明）。

We determined absolute and relative criticality values for each country for which all the data used in computing parameters was available (108 countries). We then used relative criticality in selecting our most critical countries, by continent. Had we used absolute criticality it would have given precedence to large nations, despite relatively mild HIV/AIDS situations.

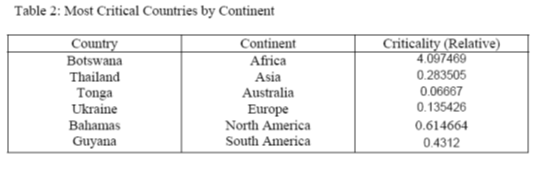
例3

The table below is the generated irrigation schedule for the repositioning of the sprinklers, given 12-hour work day for a rancher. Each pipe is set in place for 5 hours.

例4

And some data processing we can get the relevant statistical data information of patient and donor characteristics for the simulation.

例5

The graft survival rates show in the following UNOS data for kidney transplants in the U.S (based on OPTN data as of 2006):

 

2、在表后对表的内容进行说明

例1

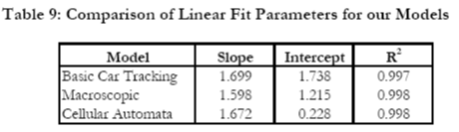
Table 9 shows linear fit parameters for all three models. Note that all three models are well described by a linear equation.

例2

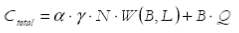
Using the cellular automata model, we compute waiting time as a function of both the number of lanes and the number of tollbooths. For a fixed L, we compare all values of Ctotal and choose the lowest one. The results of this method are presented in Table6.

例3

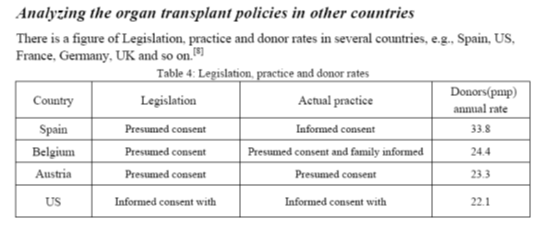
According to the above data, we can see that many of the European countries have the high rates of the donor, particularly in Spain. This phenomenon shows that the organ transplant is also hot in Europe. Although the relevant policies and statutes in these countries are less comprehensive than that in U.S, there still a lot what U.S could learn from. Here, we mainly analyze the organ transplant policies in Spain, U.K and Korea this three countries.

……The population contained in each region is summarized in table 1.（在表后对数据的内容进行总结）

例4

图表的解释部分

As indicated in Table 6, there is fairly good agreement between the recommended number of booths for a typical day and for peak hours. However, we note that the optimal booth number for a typical day never exceeds that for rush hour. Rush hour seems to require slightly more booths than a typical day in order for the plaza to operate most efficiently.

Each value in Table 6 is representative of approximately 20 trials. Through these trials, we noted a remarkable stability in our model. Despite the stochastic nature of our algorithm, each number of lanes was almost always optimized to the same number of tollbooths. There were a handful of exceptions; they occurred exclusively for small numbers of highway lanes (< 3 lanes). Integer values are presented in Table 6 only because fractional tollbooths have no physical meaning.

3、表前表后有引入引出 ，且中间对两表之间进行比较

例1

表的解释部分

We can obtain the data which is involved with the status of the American Organ

Transplant from the data banks. We have collected the demand of the various organs in United States to date, the annual donors，transplants and the demand (Here taking the kidney for example, by years 1995-2006)

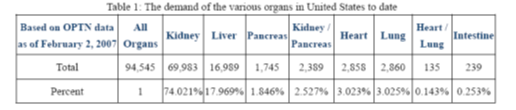
From the above table1, we can see that the kidney accounts for 73% in the

total of the organ transplants. It accounts for a very large proportion as a most important organ which can be transplanted. Therefore, we only need to discuss the status of the kidney transplant here, being able to achieve the analysis and research on the organ transplant.

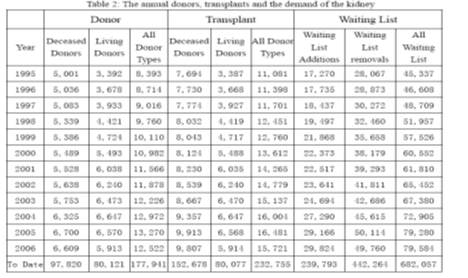
According to the above data, we can get the figures as follow:

例2

So after many times simulation under the conditions discussed above, we obtain statistic results as follow:

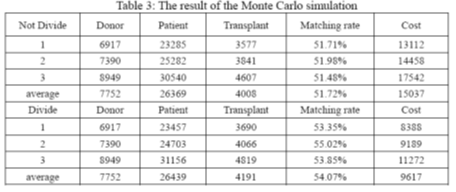
表的解释部分

By analyzing the above result, we can find: When there are more donors (more

resources), the number of transplant will increase obviously, and the matching rate changes only a little; When the network is divided into 11 regions (small networks), the costs of the transport and preservation of the organ will be reduced greatly.

 

例3

Table 7 reports the general patient statistics under each regime in the columns. The first column in these tables reports the total live donor transplants as percentage of the population size, which is the sum of next two columns, transplants from own compatible donor and transplants from trades. The forth column is the percentage of patients upgraded to the top of the waitlist as heads of w-chains. The fifth and sixth columns report the quality of matches in the live donor transplants: the risk of graft failure relative to the risk under no-exchange mechanism with population size n=400 is reported in the fifth column and the number of HLA mismatches for an average transplant is reported in the sixth column. In the table 8, we change the n into 200.

表与表之间的比较

By comparison, we can found that the matching proportion become little and the matching quality will get worse as the total number of the patients decrease. The result is consistent with the reality. The 30% probability of the waiting list or low quality exchange is an adjustable parameter.

例4

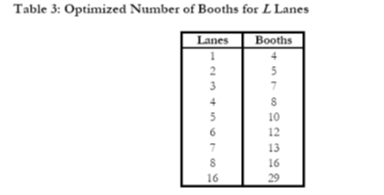
表与表的比较

Also, we wish to explore the situation in which there is one lane per booth:

例5

The parameters we choose to modify are p (probability of advancement), 'delay' (number of time steps required to serve a vehicle in a tollbooth), and q (the probability that a flagged vehicle opts to attempt a turn). The results of this analysis are presented in Table 7. Since we have used six lanes as our standard test case, we continue with this choice here.

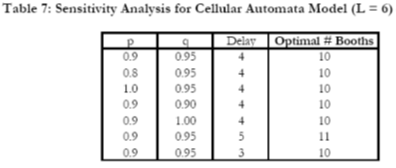
As indicated in Table 7, our cellular automata model is relatively insensitive to both p and q. Changes of ± 11% and ± 5.2% in p and q, respectively, had no effect on the optimal number of tollbooths for a six lane highway. On the other hand, increasing the delay time by 25% shifted the optimal number of booths from 10 to 11 (10%). Decreasing the delay by 25% had no effect on the solution. Perhaps additional work could lead to an elucidation of the relation between delay and optimal booth number that could help stabilize the cellular automata model.