文章目录
github链接:https://nbviewer.jupyter.org/github/shiqi-lu/Learn-AI/blob/master/pytorch_deepshare/week1.ipynb
1.PyTorch简介与安装
Q:如何安装Pytorch?
- 安装anaconda:
conda install pytorch torchvision - 测试是否安装成功:
>>> import torch
>>> torch.cuda.is_available()
True
>>> torch.__version__
'1.3.1'
2.张量简介与创建
Q:张量是什么?
- 一个多维数组,它是标量、向量、矩阵的高维拓展

Q:Pytorch中的Variable是什么?与Tensor的关系是什么?
- Variable是torch.autograd中的数据类型主要用于封装Tensor,进行自动求导
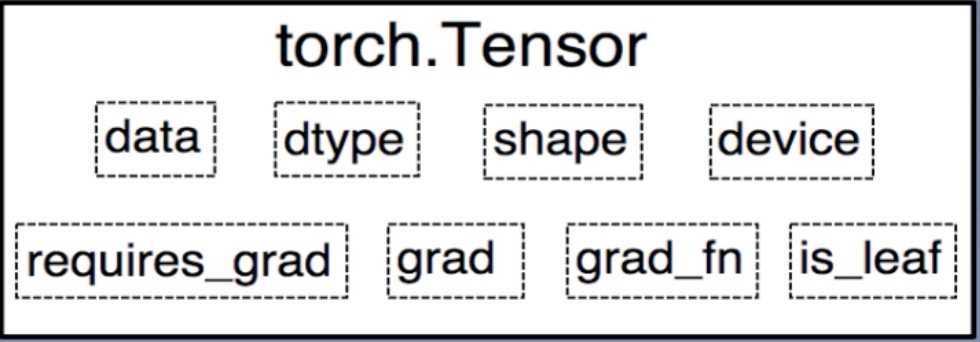
- data:被包装的Tensor
- grad:data的梯度
- grad_fn:创建Tensor的Function,是自动求导的关键
- requires_grad:指示是否需要梯度
- is_leaf:指示是否是叶子结点(张量)

Q:Pytorch中的Tensor是什么?
- PyTorch 0.4.0开始,Variable并入Tensor
- dtype: 张量的数据类型,如torch.FloatTensor, torch.cuda.FloatTensor
- shape: 张量的形状,如(64,3, 224, 224)
- device: 张量所在设备,GPU/CPU,是加速的关键
Q:Tensor的函数原型是怎样?
torch.tensor(data, dtype=None, device=None, requires_grad=False, pin_memory=False)- 功能:从data创建tensor
- data: 数据,可以是list,numpy
- dtype: 数据类型,默认与data一致
- device: 所在设备,cuda/cpu
- requires_grad: 是否需要梯度
- pin_memory:是否存于锁页内存
Q:通过torch.tensor创建Tensor的代码是什么?
import torch
import numpy as np
arr = np.ones((3, 3))
print(arr)
print('ndarray的数据类型:', arr.dtype)
t = torch.tensor(arr)
print(t)
# 放到gpu上
t = torch.tensor(arr, device='cuda')
print(t)
[[1. 1. 1.]
[1. 1. 1.]
[1. 1. 1.]]
ndarray的数据类型: float64
tensor([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]], dtype=torch.float64)
tensor([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]], device='cuda:0', dtype=torch.float64)
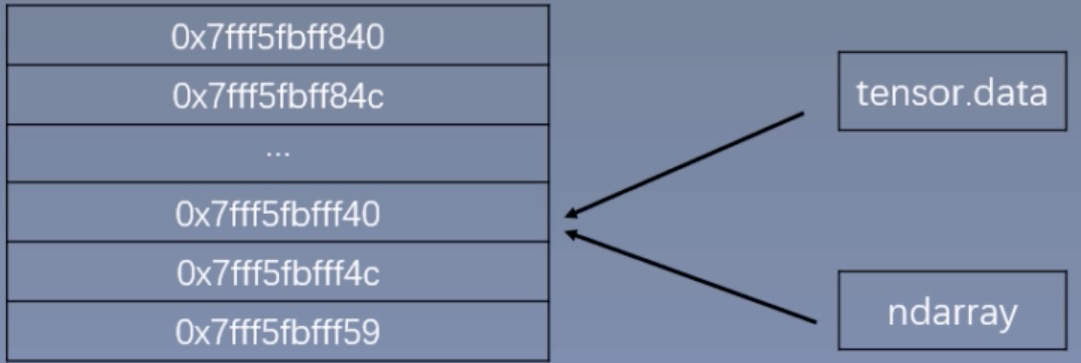
Q:如何通过torch.from_numpy创建张量?
- 函数原型:
torch.from_numpy(ndarray) - 功能:从numpy创建tensor
- 注意事项:从torch.from_numpy创建的tensor于原ndarray共享内存,当修改其中一个的数据,另外一个也将会被改动
arr = np.array([[1,2,3],[4,5,6]])
t = torch.from_numpy(arr)
print("numpy array:")
print(arr)
print("tensor:")
print(t)
print("修改arr:")
arr[0, 0] = 0
print("numpy array:")
print(arr)
print("tensor:")
print(t)
print("修改tensor:")
arr[1, 1] = -10
print("numpy array:")
print(arr)
print("tensor:")
print(t)
numpy array:
[[1 2 3]
[4 5 6]]
tensor:
tensor([[1, 2, 3],
[4, 5, 6]])
修改arr:
numpy array:
[[0 2 3]
[4 5 6]]
tensor:
tensor([[0, 2, 3],
[4, 5, 6]])
修改tensor:
numpy array:
[[ 0 2 3]
[ 4 -10 6]]
tensor:
tensor([[ 0, 2, 3],
[ 4, -10, 6]])
Q:如何通过torch.zeros或torch.ones创建张量?
- 函数原型:
torch.zeros(*size, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) - 函数原型:
torch.ones(*size, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) - 功能:依size创建全0张量和全1
- size:张量的形状
- out:输出的张量,貌似其原始类型必须为tensor,通过out得到的和返回值得到的是完全一样的,相当于赋值
- layout:内存中布局形式,有strided,sparse_coo等
- device:所在设备,gpu/cpu
- requires_grad: 是否需要梯度
out_t = torch.tensor([1])
t = torch.zeros((3,3), out=out_t)
print(t)
print(out_t)
print(id(t), id(out_t), id(t) == id(out_t))
tensor([[0, 0, 0],
[0, 0, 0],
[0, 0, 0]])
tensor([[0, 0, 0],
[0, 0, 0],
[0, 0, 0]])
140556294938560 140556294938560 True
Q:如何通过torch.zeros_like或torch.ones_like创建张量?
- 函数原型:
torch.zeros_like(input, dtype=None, layout=None, device=None, requires_grad=False) - 函数原型:
torch.ones_like(input, dtype=None, layout=None, device=None, requires_grad=False) - 功能:依input形状创建全0张量或全1,input是一个tensor类型
- input:创建与input同形状的全0张量
t = torch.empty(2,3)
print(torch.zeros_like(t))
print(torch.ones_like(t))
tensor([[0., 0., 0.],
[0., 0., 0.]])
tensor([[1., 1., 1.],
[1., 1., 1.]])
Q:如何通过torch.full创建张量?
torch.full(size, fill_value, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False)torch.full_like(input, fill_value, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False, memory_format=torch.preserve_format)- 功能:创建全等张量
- size: 张量的形状,如(3,3)
- fill_value: 张量的值
torch.full((3,3), 8)
tensor([[8., 8., 8.],
[8., 8., 8.],
[8., 8., 8.]])
Q:如何通过torch.arange创建等差数列的1维张量?
- 函数原型:
torch.arange(start=0, end, step=1, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) - 功能:创建等差为1的张量
- 注意事项:数值区间为[start, end)
- start: 数列起始值
- end: 数列“结束值”
- step: 数列公差,默认为1
torch.arange(2,10,2)
tensor([2, 4, 6, 8])
Q:如何通过torch.linspace创建均分数列张量
- 函数原型:
torch.linspace(start=0, end, steps=100, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) - 功能:创建均分的1维张量
- 注意事项:数值区间为[start, end]
- start: 数列起始值
- end: 数列结束值
- steps: 数列长度
- 步长为:(end-start)/(steps-1)
torch.linspace(2, 10, 7)
tensor([ 2.0000, 3.3333, 4.6667, 6.0000, 7.3333, 8.6667, 10.0000])
Q:如何通过torch.logspace创建对数均分的1维张量?
- 函数原型:
torch.logspace(start, end, steps=100, base=10.0, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) - 功能:创建对数均分的1维张量
- 注意事项:长度为steps,底为base
- base: 对数函数的低,默认为10
Q:如何通过torch.eye创建单位对角矩阵?
- 函数原型:
torch.eye(n, m=None, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) - 功能:创建单位对角矩阵(2维张量)
- 注意事项:默认为方阵
- n: 矩阵行数
- m: 矩阵列数
Q:如何通过torch.normal生成正态分布的张量?
- 函数原型:
torch.normal(mean, std, *, generator=None, out=None) - 功能:生成正态分布(高斯分布)
- mean: 均值
- std: 标准差
- 因mean和std可以分别为标量和张量,有4种不同的组合
# mean:张量 std: 张量
# 其中t[i]是从mean[i],std[i]的标准正态分布中采样得来
mean = torch.arange(1, 5, dtype=torch.float)
std = torch.arange(1, 5, dtype=torch.float)
t = torch.normal(mean, std)
print("mean:{}\nstd:{}".format(mean, std))
print(t)
print()
# mean:标量 std: 标量,此时要指定size大小
t_normal = torch.normal(0., 1., size=(4,))
print(t_normal)
print()
# mean:张量 std: 标量
mean = torch.arange(1, 5, dtype=torch.float)
std = 1
t_normal = torch.normal(mean, std)
print("mean:{}\nstd:{}".format(mean, std))
print(t_normal)
mean:tensor([1., 2., 3., 4.])
std:tensor([1., 2., 3., 4.])
tensor([ 0.6063, 2.9914, 4.0138, -0.5877])
tensor([ 1.1977, -0.1746, 1.5572, -1.1905])
mean:tensor([1., 2., 3., 4.])
std:1
tensor([0.7165, 1.5649, 3.2308, 3.2504])
Q:如何创建标准正态分布的张量?
torch.randn(*size, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) → Tensortorch.randn_like(input, dtype=None, layout=None, device=None, requires_grad=False, memory_format=torch.preserve_format) → Tensor- size:张量的形状
print(torch.randn(4))
print(torch.randn(2,3))
tensor([-0.2387, -0.3638, 0.3597, 0.1225])
tensor([[ 0.4709, 0.8593, -0.5970],
[-0.1133, 0.3273, 0.0106]])
Q:如何生成均匀分布和整数均匀分布的张量?
- 在[0,1)区间上,生成均匀分布
torch.rand(*size, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) → Tensortorch.rand_like(input, dtype=None, layout=None, device=None, requires_grad=False, memory_format=torch.preserve_format) → Tensor- 在[low, high)区间生成整数均匀分布
torch.randint(low=0, high, size, *, generator=None, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False) → Tensortorch.randint_like(input, low=0, high, dtype=None, layout=torch.strided, device=None, requires_grad=False, memory_format=torch.preserve_format) → Tensor- 其中size是张量形状
Q:如何生成从0到n-1的随机排列?
torch.randperm(n, out=None, dtype=torch.int64, layout=torch.strided, device=None, requires_grad=False) → LongTensor- n是张量的长度
- 经常用于生成乱序索引
Q:如何生成一个伯努利分布的张量?
torch.bernoulli(input, *, generator=None, out=None) → Tensor- 以input为概率,生成伯努利分布(0-1分布,两点分布)
3.张量操作与线性回归
张量的操作:拼接、切分、索引和变换
Q:如何用torch.cat对张量进行拼接?
torch.cat(tensors, dim=0, out=None) → Tensor- 功能:将张量按维度dim进行拼接
- tensors: 张量序列
- dim:要拼接的维度
t = torch.randn(2,3)
print(t)
t1 = torch.cat([t,t], dim=0)
print(t1)
print("shape:", t1.shape)
t2 = torch.cat([t,t], dim=1)
print(t2)
print("shape:", t2.shape)
# dim是指在哪个方向上进行叠加
tensor([[-0.6851, 0.0099, -1.4586],
[ 0.2965, 0.4991, -0.4938]])
tensor([[-0.6851, 0.0099, -1.4586],
[ 0.2965, 0.4991, -0.4938],
[-0.6851, 0.0099, -1.4586],
[ 0.2965, 0.4991, -0.4938]])
shape: torch.Size([4, 3])
tensor([[-0.6851, 0.0099, -1.4586, -0.6851, 0.0099, -1.4586],
[ 0.2965, 0.4991, -0.4938, 0.2965, 0.4991, -0.4938]])
shape: torch.Size([2, 6])
Q:如何用torch.stack对张量进行拼接?
torch.stack(tensors, dim=0, out=None) → Tensor- 功能:在新创建的维度dim上进行拼接
- tensors:张量序列
- dim:要拼接的维度
- 注意:cat不会扩张张量的维度,stack会扩张,相当于insert
t = torch.randn(2,3)
print(t)
t1 = torch.stack([t,t], dim=0)
print(t1)
print("shape:", t1.shape)
tensor([[ 0.6266, 0.8918, 0.6165],
[ 1.1646, -1.8152, -0.7309]])
tensor([[[ 0.6266, 0.8918, 0.6165],
[ 1.1646, -1.8152, -0.7309]],
[[ 0.6266, 0.8918, 0.6165],
[ 1.1646, -1.8152, -0.7309]]])
shape: torch.Size([2, 2, 3])
Q:如何用torch.chunk对切分张量?
torch.chunk(input, chunks, dim=0) → List of Tensors- 功能:将张量按维度dim进行平均切分
- 返回值:张量列表
- 注意事项:若不能整除,最后一份张量小于其它张量
- input:要切分的张量
- chunks:要切分的份数
- dim:要切分的维度
a = torch.ones((2,7))
print(a)
list_of_tensors = torch.chunk(a, dim=1, chunks=3)
for i, t in enumerate(list_of_tensors):
print(f"第{i}个张量:")
print(t)
# 切分后的长度的计算方式为:7/3向上取整为3
tensor([[1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1.]])
第0个张量:
tensor([[1., 1., 1.],
[1., 1., 1.]])
第1个张量:
tensor([[1., 1., 1.],
[1., 1., 1.]])
第2个张量:
tensor([[1.],
[1.]])
Q:如何用torch.split对张量进行切分?
torch.split(tensor, split_size_or_sections, dim=0)- 功能:将张量按维度dim进行平均切分
- 返回值:张量列表
- tensor:要切分的张量
- split_size_or_sections:为int时,表示每一份的长度;为list时,按list元素切分,list元素和必须为该维度的长度
- dim:要切分的维度
a = torch.ones((2,7))
print(a)
list_of_tensors = torch.split(a, [2,4,1], dim=1)
for i, t in enumerate(list_of_tensors):
print(f"第{i}个张量:")
print(t)
tensor([[1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1.]])
第0个张量:
tensor([[1., 1.],
[1., 1.]])
第1个张量:
tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.]])
第2个张量:
tensor([[1.],
[1.]])
Q:如何在dim维度上,按index索引数据?
torch.index_select(input, dim, index, out=None) → Tensor- 返回值:按index索引数据拼接的张量
- input:要索引的张量
- dim:要索引的维度
- index:要索引数据的序号
t = torch.randint(0,9, size=(3,3))
idx = torch.tensor([0,2], dtype=torch.long)
t_select = torch.index_select(t, dim=0, index=idx)
print(t)
print(idx)
print(t_select)
tensor([[1, 2, 8],
[2, 3, 0],
[0, 2, 0]])
tensor([0, 2])
tensor([[1, 2, 8],
[0, 2, 0]])
Q:如何对张量按mask中的True进行索引?
torch.masked_select(input, mask, out=None) → Tensor- 返回值:一维张量
- input:要索引的张量
- mask:与input同形状的布尔类型张量
t = torch.randint(0, 9, size=(3, 3))
print(t)
mask = t.le(5) # le是小于等于,还有lt,gt,ge
print(mask)
t_select = torch.masked_select(t, mask)
print(t_select)
tensor([[2, 5, 0],
[5, 8, 5],
[2, 8, 5]])
tensor([[ True, True, True],
[ True, False, True],
[ True, False, True]])
tensor([2, 5, 0, 5, 5, 2, 5])
Q:如何改变张量的形状?
torch.reshape(input, shape) → Tensor- 注意事项:当张量在内存中是连续时,新张量与input共享数据内存
- input:要变换的张量
- shape:新张量的形状,允许某个维度为-1,意味着这个维度根据其它的算出来的
t = torch.randperm(8)
t_reshape = torch.reshape(t, (2,4))
print(t)
print(t_reshape)
tensor([2, 0, 7, 5, 6, 4, 3, 1])
tensor([[2, 0, 7, 5],
[6, 4, 3, 1]])
Q:如何交换张量的两个维度?
torch.transpose(input, dim0, dim1) → Tensor- input:要交换的张量
- dim0,dim1:要交换的维度
- 若为2维张量转置,即矩阵转置,可使用
torch.t(input) → Tensor,等价于torch.transpose(input, 0, 1)
t = torch.rand((2,3,4))
t_transpose = torch.transpose(t, dim0=1,dim1=2)
print(t)
print(t_transpose)
tensor([[[0.8657, 0.5869, 0.1105, 0.4381],
[0.7276, 0.6606, 0.3778, 0.3643],
[0.6180, 0.6693, 0.9983, 0.4252]],
[[0.3526, 0.6365, 0.6643, 0.5310],
[0.4653, 0.5056, 0.1065, 0.7873],
[0.6175, 0.6650, 0.1325, 0.5837]]])
tensor([[[0.8657, 0.7276, 0.6180],
[0.5869, 0.6606, 0.6693],
[0.1105, 0.3778, 0.9983],
[0.4381, 0.3643, 0.4252]],
[[0.3526, 0.4653, 0.6175],
[0.6365, 0.5056, 0.6650],
[0.6643, 0.1065, 0.1325],
[0.5310, 0.7873, 0.5837]]])
Q:如何压缩长度为1的维度(轴)?
torch.squeeze(input, dim=None, out=None) → Tensor- dim: 若为None,移除所有长度为1的轴;若指定维度,当且仅当该轴长度为1时,可以被移除
t = torch.rand((1, 2, 3, 1))
t_sq = torch.squeeze(t)
t_0 = torch.squeeze(t, dim=0)
t_1 = torch.squeeze(t, dim=1)
print(t.shape)
print(t_sq.shape)
print(t_0.shape)
print(t_1.shape)
torch.Size([1, 2, 3, 1])
torch.Size([2, 3])
torch.Size([2, 3, 1])
torch.Size([1, 2, 3, 1])
Q:如何根据dim扩展维度?
torch.unsqueeze(input, dim) → Tensor- dim:扩展的维度
t = torch.tensor([1, 2, 3, 4])
print(t)
t1 = torch.unsqueeze(t, 0)
print(t1)
t2 = torch.unsqueeze(t, 1)
print(t2)
tensor([1, 2, 3, 4])
tensor([[1, 2, 3, 4]])
tensor([[1],
[2],
[3],
[4]])
张量的数学运算
Q:有哪些常见的数学运算?
- 一、加减乘除
- torch.add()
- torch.addcdiv()
- torch.addcmul()
- torch.sub()
- torch.div()
- torch.mul()
- 二、对数,指数,幂函数
- torch.log(input, out=None)
- torch.log10(input, out=None)
- torch.log2(input, out=None)
- torch.exp(input, out=None)
- torch.pow()
- 三、三角函数
- torch.abs(input, out=None)
- torch.acos(input, out=None)
- torch.cosh(input, out=None)
- torch.cos(input, out=None)
- torch.asin(input, out=None)
- torch.atan(input, out=None)
- torch.atan2(input, other, out=None)
Q:如何逐元素计算input + alpha x other?
torch.add(input, other, *, alpha=1, out=None)- input:第一个张量
- alpha:乘项因子
- other:第二个张量
t_0 = torch.randn((3, 3))
t_1 = torch.ones_like(t_0)
t_add = torch.add(t_0, t_1, alpha=10)
print("t_0:\n{}\nt_1:\n{}\nt_add_10:\n{}".format(t_0, t_1, t_add))
t_0:
tensor([[ 0.5570, -0.4743, 1.0113],
[-1.2665, 0.1997, -0.6957],
[-0.0714, -0.7002, -1.4687]])
t_1:
tensor([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
t_add_10:
tensor([[10.5570, 9.5257, 11.0113],
[ 8.7335, 10.1997, 9.3043],
[ 9.9286, 9.2998, 8.5313]])
Q:如何计算 out i = input i + value × tensor 1 i × tensor 2 i \text { out }_{i}=\text { input }_{i}+\text { value } \times \text { tensor } 1_{i} \times \text { tensor } 2_{i} out i= input i+ value × tensor 1i× tensor 2i
torch.addcmul(input, tensor1, tensor2, *, value=1, out=None) → Tensor
Q:如何计算 out i = input i + value × tensor 1 tensor 2 i \text { out }_{i}=\text { input }_{i}+\text { value } \times \frac{\text { tensor } 1}{\text { tensor } 2_{i}} out i= input i+ value × tensor 2i tensor 1
torch.addcdiv(input, tensor1, tensor2, *, value=1, out=None) → Tensor
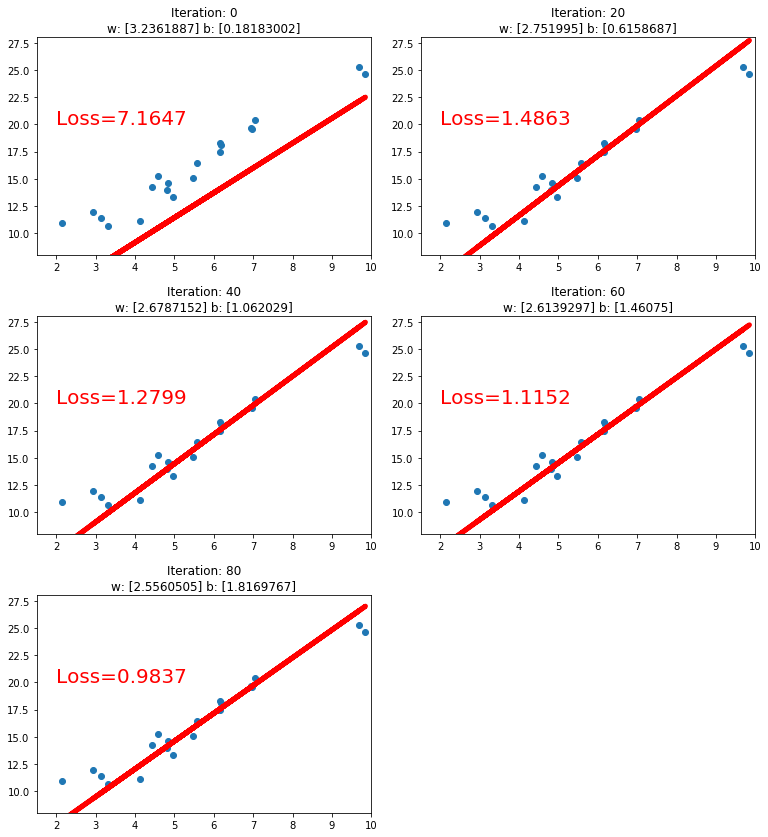
线性回归的Pytorch实现
import torch
import matplotlib.pyplot as plt
torch.manual_seed(10)
lr = 0.05 # 学习率
# 创建训练数据
x = torch.rand(20, 1) * 10 # x data (tensor), shape=(20, 1)
y = 2*x + (5 + torch.randn(20, 1)) # y data (tensor), shape=(20, 1)
# 构建线性回归参数的初始值
w = torch.randn((1), requires_grad=True)
b = torch.zeros((1), requires_grad=True)
for iteration in range(1000):
# 前向传播,计算y_pred=w * x+b
wx = torch.mul(w, x)
y_pred = torch.add(wx, b)
# 计算 MSE loss
loss = (0.5 * (y - y_pred) ** 2).mean()
# 反向传播
loss.backward()
# 更新参数
b.data.sub_(lr * b.grad)
w.data.sub_(lr * w.grad)
# 清零张量的梯度
w.grad.zero_()
b.grad.zero_()
# 绘图
if iteration % 20 == 0:
plt.scatter(x.data.numpy(), y.data.numpy())
plt.plot(x.data.numpy(), y_pred.data.numpy(), 'r-', lw=5)
plt.text(2, 20, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'})
plt.xlim(1.5, 10)
plt.ylim(8, 28)
plt.title(f"Iteration: {iteration}\nw: {w.data.numpy()} b: {b.data.numpy()}")
plt.pause(0.5)
if loss.data.numpy() < 1:
break
4.计算图与动态图机制
Q:计算图是什么?
- 用来描述运算的有向无环图
- 有两个主要元素:结点(Node)和边(Edge)
- 结点表示数据,如向量、矩阵、张量,边表示运算,如加减乘除卷积等
Q:如何用计算图表示 y = ( x + w ) ∗ ( w + 1 ) y = (x+w)*(w+1) y=(x+w)∗(w+1)?
- a = x + w , b = w + 1 , y = a ∗ b a = x + w, b = w + 1, y = a * b a=x+w,b=w+1,y=a∗b

Q:如何用计算图进行梯度求导,如 y = ( x + w ) ∗ ( w + 1 ) y = (x+w)*(w+1) y=(x+w)∗(w+1)
- a = x + w , b = w + 1 , y = a ∗ b a = x + w, b = w + 1, y = a * b a=x+w,b=w+1,y=a∗b
- ∂ y ∂ w = ∂ y ∂ a ∂ a ∂ w + ∂ y ∂ b ∂ b ∂ w = b ∗ 1 + a ∗ 1 = b + a = ( w + 1 ) + ( x + w ) = 2 ∗ w + x + 1 = 2 ∗ 1 + 2 + 1 = 5 \begin{aligned} \frac{\partial \mathrm{y}}{\partial w} &=\frac{\partial \mathrm{y}}{\partial a} \frac{\partial a}{\partial w}+\frac{\partial \mathrm{y}}{\partial b} \frac{\partial b}{\partial w} \\ &=b * 1+\mathrm{a} * 1 \\ &=\mathrm{b}+\mathrm{a} \\ &=(\mathrm{w}+1)+(\mathrm{x}+\mathrm{w}) \\ &=2 * \mathrm{w}+\mathrm{x}+1 \\ &=2 * 1+2+1=5\end{aligned} ∂w∂y=∂a∂y∂w∂a+∂b∂y∂w∂b=b∗1+a∗1=b+a=(w+1)+(x+w)=2∗w+x+1=2∗1+2+1=5
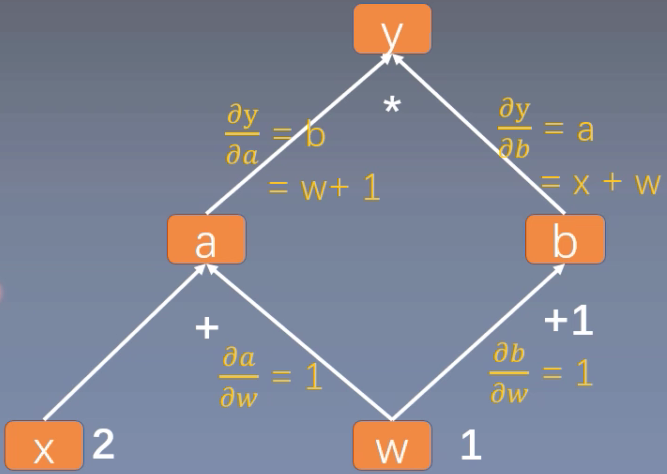
- y对w求导在计算图中其实就是找到y到w的所有路径上的导数,进行求和
Q:叶子结点是什么?

- 用户创建的结点称为叶子结点,如X和W
- torch.Tensor中有is_leaf指示张量是否为叶子结点
- 设置叶子结点主要是为了节省内存,因为非叶子结点的梯度在反向传播后会被释放掉
- 若需要保留非叶子结点的梯度,可使用retain_grad()方法
Q:torch.Tensor中的grad_fn作用是什么?
- 记录创建该张量时所用的方法(函数)

- y.grad_fn = <MulBackward0>
- a.grad_fn = <AddBackward0>
Q: y = ( x + w ) ∗ ( w + 1 ) y = (x+w)*(w+1) y=(x+w)∗(w+1)计算图的代码示例,求解y对w的梯度?
import torch
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
a = torch.add(w, x)
# 若需要保留非叶子结点a的梯度,否则调用a.grad时为None
# a.retain_grad()
b = torch.add(w, 1)
y = torch.mul(a, b)
y.backward()
print(w.grad)
# 查看叶子结点
print("\nis_leaf:\n", w.is_leaf, x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)
# 查看梯度
print("\ngradient:\n", w.grad, x.grad, a.grad, b.grad, y.grad)
# 查看 grad_fn
print("\ngrad_fn:\n", w.grad_fn, x.grad_fn, a.grad_fn, b.grad_fn, y.grad_fn)
tensor([5.])
is_leaf:
True True False False False
gradient:
tensor([5.]) tensor([2.]) None None None
grad_fn:
None None <AddBackward0 object at 0x7fd54938bb00> <AddBackward0 object at 0x7fd5285f4c50> <MulBackward0 object at 0x7fd5285f4be0>
5.autograd与逻辑回归
Q:torch.autograd.backward是什么?
- torch.autograd.backward(tensors: Union[torch.Tensor, Sequence[torch.Tensor]], grad_tensors: Union[torch.Tensor, Sequence[torch.Tensor], None] = None, retain_graph: Optional[bool] = None, create_graph: bool = False, grad_variables: Union[torch.Tensor, Sequence[torch.Tensor], None] = None) → None
- 功能:自动求取梯度
- tensors:用于求导的张量,如loss
- retain_graph:保存计算图,若不保存,则紧接着再调用一次backward()会报错
- create_graph:创建导数计算图,用于高阶求导
- grad_tensors:多梯度权重
Q:torch.autograd.backward中的retain_graph的代码示例?
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
a = torch.add(w, x)
b = torch.add(w, 1)
y = torch.mul(a, b)
y.backward(retain_graph=True
)
print(w.grad)
y.backward()
print(w.grad)
tensor([5.])
tensor([10.])
Q:torch.autograd.backward中的grad_tensors的代码示例?
w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)
a = torch.add(w, x) # retain_grad()
b = torch.add(w, 1)
y0 = torch.mul(a, b) # y0 = (x+w) * (w+1)
y1 = torch.add(a, b) # y1 = (x+w) + (w+1) dy1/dw = 2
loss = torch.cat([y0, y1], dim=0) # [y0, y1]
grad_tensors = torch.tensor([1., 2.])
# gradient 传入 torch.autograd.backward()中的grad_tensors
loss.backward(gradient=grad_tensors)
# 实际上相当于1*y0导数+2*y1导数
print(w.grad)
tensor([9.])
Q:torch.autograd.grad是什么?
- torch.autograd.grad(outputs: Union[torch.Tensor, Sequence[torch.Tensor]], inputs: Union[torch.Tensor, Sequence[torch.Tensor]], grad_outputs: Union[torch.Tensor, Sequence[torch.Tensor], None] = None, retain_graph: Optional[bool] = None, create_graph: bool = False, only_inputs: bool = True, allow_unused: bool = False) → Tuple[torch.Tensor, …]
- 功能:求取梯度
- outputs:用于求导的张量,如loss
- inputs:需要梯度的张量
- create_graph:创建导数计算图,用于高阶求导
- retain_graph:保存计算图
- grad_outputs:多梯度权重
Q:如何使用torch.autograd.grad对 y = x 2 y=x^2 y=x2进行一阶和二阶求导?
x = torch.tensor([3.], requires_grad=True)
y = torch.pow(x, 2) # y = x**2
# grad_1 = dy/dx = 2x = 2 * 3 = 6
grad_1 = torch.autograd.grad(y, x, create_graph=True)
print(grad_1)
# grad_2 = d(dy/dx)/dx = d(2x)/dx = 2
# grad_1的返回值是元组,所以要取出第一个
grad_2 = torch.autograd.grad(grad_1[0], x)
print(grad_2)
(tensor([6.], grad_fn=<MulBackward0>),)
(tensor([2.]),)
Q:autograd的3点使用小贴士是什么?
- 1.梯度不自动清零,每次传播时会一直叠加上去,所以使用梯度之后要手动进行清零,即w.grad.zero_(),其中下划线表示inplace(原地)操作
- 2.依赖于叶子结点的节点,requires_grad默认为True
- 3.叶子结点不可执行in-place
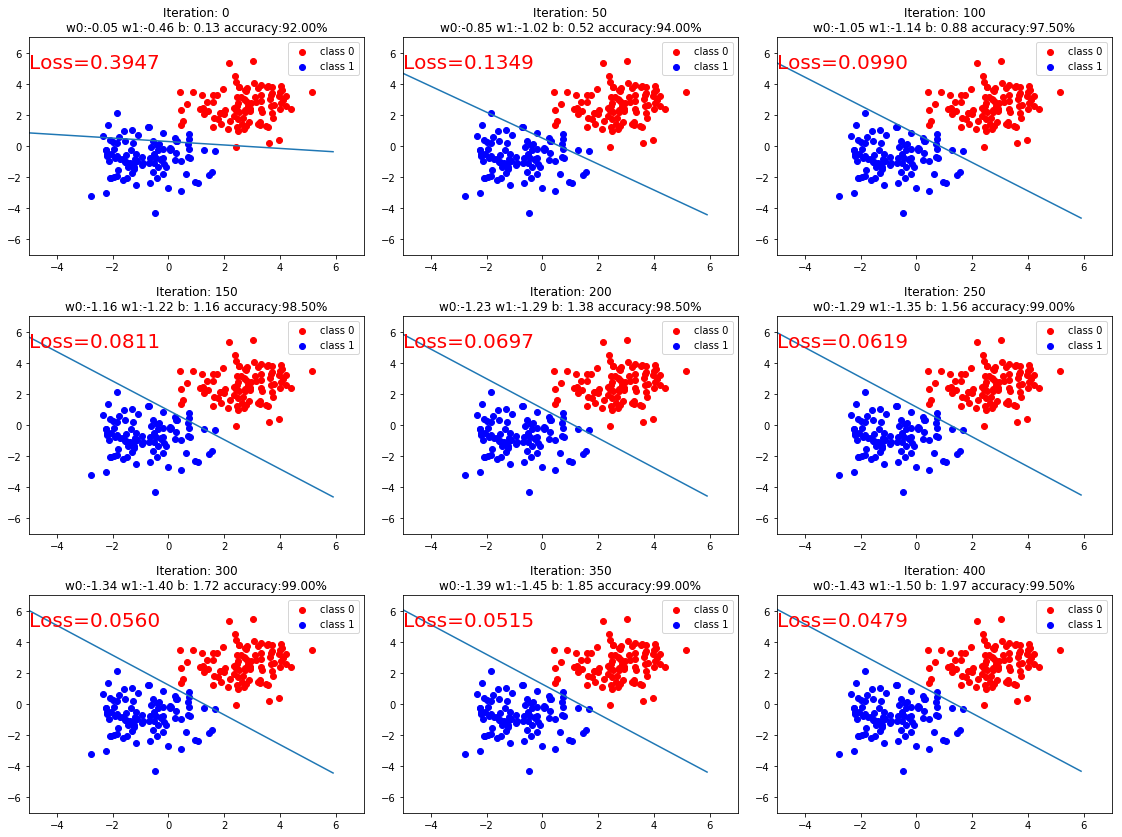
Q:逻辑回归的pytorch代码实现是什么?
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
torch.manual_seed(10)
# 生成数据
sample_nums = 100
mean_value = 1.7
bias = 1
n_data = torch.ones(sample_nums, 2)
# 类别0 数据 shape=(100, 2)
x0 = torch.normal(mean_value * n_data, 1) + bias
# 类别0 标签 shape=(100)
y0 = torch.zeros(sample_nums)
# 类别1 数据 shape=(100, 2)
x1 = torch.normal(-mean_value * n_data, 1) + bias
# 类别1 标签 shape=(100)
y1 = torch.ones(sample_nums)
train_x = torch.cat((x0, x1), 0)
train_y = torch.cat((y0, y1), 0)
# 选择模型
class LR(nn.Module):
def __init__(self):
super(LR, self).__init__()
self.features = nn.Linear(2, 1)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
x = self.features(x)
x = self.sigmoid(x)
return x
# 实例化逻辑回归模型
lr_net = LR()
# 选择损失函数,交叉熵损失
loss_fn = nn.BCELoss()
# 选择优化器
lr = 0.01 # 学习率
optimizer = torch.optim.SGD(lr_net.parameters(), lr=lr, momentum=0.9)
# 模型训练
for iteration in range(1000):
# 前向传播
y_pred = lr_net(train_x)
# 计算loss
loss = loss_fn(y_pred.squeeze(), train_y)
# 反向传播
loss.backward()
# 更新参数
optimizer.step()
# 清空梯度
optimizer.zero_grad()
# 绘图
if iteration % 50 == 0:
# 以0.5为阈值进行分类
mask = y_pred.ge(0.5).float().squeeze()
# 计算正确预测的样本个数
correct = (mask == train_y).sum()
# 计算分类准确率
acc = correct.item() / train_y.size(0)
plt.scatter(x0.data.numpy()[:, 0], x0.data.numpy()[:, 1], c='r', label='class 0')
plt.scatter(x1.data.numpy()[:, 0], x1.data.numpy()[:, 1], c='b', label='class 1')
w0, w1 = lr_net.features.weight[0]
w0, w1 = float(w0.item()), float(w1.item())
plot_b = float(lr_net.features.bias[0].item())
plot_x = np.arange(-6, 6, 0.1)
plot_y = (-w0 * plot_x - plot_b) / w1
plt.xlim(-5, 7)
plt.ylim(-7, 7)
plt.plot(plot_x, plot_y)
plt.text(-5, 5, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size':20, 'color':'red'})
plt.title("Iteration: {}\nw0:{:.2f} w1:{:.2f} b: {:.2f} accuracy:{:.2%}".format(iteration, w0, w1, plot_b, acc))
plt.legend()
plt.show()
plt.pause(0.5)
if acc > 0.99:
break






















 4378
4378











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








