看了好久,感觉明白一些,记录一下
Steger提取激光中心线的原理大致为:
首先将激光图片高斯模糊一下,卷积核大小要为激光线条的宽度,将激光的截面光强分布变为理想的正态函数。
实际的激光线条有一个宽度

要变为理想无宽度的

然后求出每一个点对应的二阶导数(hessian矩阵)、一阶导数的值,来构造一个该像素点附近的光强分布函数(泰勒展开)。
(一阶、二阶导数通过构造卷积核来计算,代码中体现)
求出二阶导数的同时,可以得到hessian矩阵。
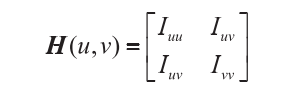
Hessian矩阵的特征值就是形容其在该点附近特征向量方向的凹凸性,特征值越大,凸性越强。
所以hessian特征值绝对值最大的对应的特征向量就是光强变化最快的方向,我们可以向这个地方去寻找最强光强的像素点。(也就是中心线上的点)
构造出当前像素附近的光强分布的多项式(泰勒展开)如下图。
e指的是当前点坐标,I(u0,v0)代表当前像素的光强值,[Iu,Iv]代表一阶导数的值,H(u,v)代表二阶导数的值,t是一个未知参数

现在已经知道了当前坐标(u0,v0)也知道了光强变化最快的方向(uu,vv),二阶导数(hessian矩阵)、一阶导数。
hessian矩阵特征值最大的对应的特征向量(uu,vv)表示梯度上升最快的方向(光强改变最快),要往这个方向改变
这个当前坐标附近的光强分布函数可以看作是关于t的一个分布函数
则可以对t求导,令导数为0的地方就是光强最强的地方(极值),也就是激光中心点。

可以改写成矩阵的形式

化简可以得到

计算出t后
(泰勒展开只能在很短的距离内适用)
如果teu和tev都小于0.5说明这个极值点就位于当前像素内。附近光强分布函数适用
如果teu和tev都很大,则说明这个光强最强点有点距离(同时附近光强分布函数不适用,不可以用t计算最强点),要跳过当前点,继续扫描距离激光中心更近的点。
代码如下
//path为一张图片的路径
std::vector<double> ProcessTool::StegerLine(std::string path)
{
Mat img0 = imread(path, 1);
//滤波去噪点,不需要可以注释掉,去掉之后灰度图要去注释
cv::medianBlur(img0, img0, 5);
cvtColor(img0, img0, CV_RGB2GRAY);
threshold(img0, img0, 0, 255, THRESH_OTSU);
Mat img;
//灰度图
//cvtColor(img0, img0, CV_BGR2GRAY);
img = img0.clone();
//高斯滤波
img.convertTo(img, CV_32FC1);
GaussianBlur(img, img, Size(5, 5), 2, 2);
//高斯卷积,得到一个山峰强度的光条图
//高斯卷积核实际上就是一个正态函数
imshow("高斯滤波",img);
waitKey(0);
/**********************************/
//构造了求导数的卷积核
/***********************************/
//这里使用的是数值计算的偏导数而非得到求导公式
Mat m1, m2;
m1 = (Mat_<float>(1, 2) << 1, -1);//x偏导一阶偏导 = f(x+1,y)-f(x,y)
m2 = (Mat_<float>(2, 1) << 1, -1);//y偏导一阶偏导 = f(x,y+1)-f(x,y)
Mat dx, dy;
//使用m1卷积 当前坐标的灰度值-(x+1)的灰度值
filter2D(img, dx, CV_32FC1, m1);//卷积
filter2D(img, dy, CV_32FC1, m2);//卷积
//二阶偏导数
Mat m3, m4, m5;
m3 = (Mat_<float>(1, 3) << 1, -2, 1);//求二阶x偏导的矩阵=f(x+1,y)+f(x-1,y)-2f(x,y)
m4 = (Mat_<float>(3, 1) << 1, -2, 1);//二阶y偏导的矩阵
m5 = (Mat_<float>(2, 2) << 1, -1, -1, 1);//二阶xy偏导矩阵=f(x+1,y+1)-f(x+1,y)-f(x,y+1)+f(x,y)
Mat dxx, dyy, dxy;
//求得对应点的偏导数值
filter2D(img, dxx, CV_32FC1, m3);
filter2D(img, dyy, CV_32FC1, m4);
filter2D(img, dxy, CV_32FC1, m5);
//hessian矩阵
double maxD = -1;
int imgcol = img.cols;
int imgrow = img.rows;
std::vector<double> Pt;
for (int i = 0; i < imgcol; i++)
{
for (int j = 0; j < imgrow; j++)
{
//全黑的时候就不计算了,大于一个阈值的时候开始计算
if (img0.at<uchar>(j, i) > 50)
{
Mat hessian(2, 2, CV_32FC1);
//得到对应点的hessian矩阵
//对每个点,构造出hessian矩阵
hessian.at<float>(0, 0) = dxx.at<float>(j, i);
hessian.at<float>(0, 1) = dxy.at<float>(j, i);
hessian.at<float>(1, 0) = dxy.at<float>(j, i);
hessian.at<float>(1, 1) = dyy.at<float>(j, i);
//特征值和特征向量
Mat eValue;
Mat eVectors;
// hessian矩阵2*2 对称矩阵, 有两个特征值
// 获取当前点的特征值和特征向量
// 存在两个特征值及对应特征向量
eigen(hessian, eValue, eVectors);
//std::cout << "eValue:" << eValue << std::endl << "eVectors:" << eVectors << std::endl;
//nx为特征值最大对应的x,ny为特征值最大对应的y
double nx, ny;
double fmaxD = 0;
//求特征值绝对值最大时对应的特征向量
//Hessian矩阵的特征值就是形容其在该点附近特征向量方向的凹凸性,特征值越大,凸性越强。
if (fabs(eValue.at<float>(0, 0)) >= fabs(eValue.at<float>(1, 0)))
{
nx = eVectors.at<float>(0, 0);
ny = eVectors.at<float>(0, 1);
fmaxD = eValue.at<float>(0, 0);
}
else
{
nx = eVectors.at<float>(1, 0);
ny = eVectors.at<float>(1, 1);
fmaxD = eValue.at<float>(1, 0);
}
// 使用泰勒展开表示光强的分布函数f(x+t*nx,y+t*ny)可以表示当前坐标附近的光强分布
// f(x+t*nx,y+t*ny) hessian矩阵特征值最大的对应的特征向量(nx,ny)表示梯度上升最快的方向(光强改变最快),要往这个方向改变
// 由于x,y,nx,ny已知,这个当前坐标附近的光强分布函数可以看作是关于t的一个分布函数
// 则可以对t求导,令导数为0的地方就是光强最强的地方(极值),也就是激光中心点。
// 如果t*nx和t*ny都小于0.5说明这个极值点就位于当前像素内,附近光强分布函数适用
// 如果t*nx和t*ny都很大,附近光强分布函数不适用,则跳过这个点,继续扫描距离激光中心更近的点
double t = -
(nx * dx.at<float>(j, i) + ny * dy.at<float>(j, i))
/
(nx * nx * dxx.at<float>(j, i) + 2 * nx * ny * dxy.at<float>(j, i) + ny * ny * dyy.at<float>(j, i));
//t* nx和t* nx代表光条中心点距离当前像素的距离
if (fabs(t * nx) <= 0.5 && fabs(t * ny) <= 0.5)
{
Pt.push_back(i);
Pt.push_back(j);
}
}
}
}
cvtColor(img0, img0, CV_GRAY2BGR);
//显示中心点
ShowLine(Pt, img0);
return Pt;
}
//显示点的函数
ShowLine(std::vector<double> Points, Mat image)
{
for (int k = 0; k < Points.size() / 2; k++)
{
Point rpt;
rpt.x = Points[2 * k + 0];
rpt.y = Points[2 * k + 1];
image.at<Vec3b>(rpt.y, rpt.x) = Vec3b(0, 0, 255);
//circle(img0, rpt, 1, Scalar(0, 0, 255));
}
cv::imshow("GetLine", image);
//cv::imwrite("output.bmp", img0);
cv::waitKey(1);
}
参考:
1.https://blog.csdn.net/jiangxing11/article/details/120056536
2.https://blog.csdn.net/Dangkie/article/details/78996761
3.Steger C. An unbiased detector of curvilinear structures. IEEE Trans Pattern Anal Mach Intell[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1998, 20(2):113-125.























 687
687

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








