计算几何 —— 二维几何基础 —— 三角形的面积

【海伦公式】

在平面内，有一个三角形，设其三边长分别为 a、b、c，面积为 S ，则有： 

其中，

double calculate(double a,double b,double c){
    double p=(a+b+c)/2;
    return sqrt( p*(p-a)*(p-b)*(p-c) );
}

【通过叉积】

对于按逆时针转的三个点 A(x1,y1)，B(x2,y2)，C(x3,y3)，设三角形面积为 S，则有：

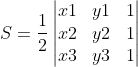
即有：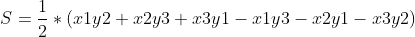

由于三个点的顺序是按照逆时针排列的，而在行列式中，交换任意两行或两列只需要在行列式前面取负一次即可，由于三角形的面积不可能是负值，因此对于任取的三个点，若想求其组成的三角形面积，只需要在上述公式前取绝对值即可

即给出任意三点的坐标，其组成的三角形的面积为：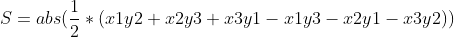

pair<int,int> node[N];
double calculate(int i,int j,int k){
    int x1=node[i].first,y1=node[i].second;
    int x2=node[j].first,y2=node[j].second;
    int x3=node[k].first,y3=node[k].second;
    int temp=abs(x1*y2+x2*y3+x3*y1-x1*y3-x2*y1-x3*y2);

    return (double)temp/2;
}