曾经叱咤风云的SVM算法,现如今虽然随着深度学习的崛起热度有所下降,但是仍然有许多的人在对他进行着研究学习和应用,曾经我也查看了许多的资料对它进行研究,但是很多文章写的都是不清不楚,具体的细节也存在不少问题,作为过来人,深刻体会到推导过程一定要写的细致且明白才好。
支持向量机的概念:给定线性可分的训练数据集,通过间隔最大化或等价地求解相应的凸二次规划问题学习得到分离超平面为:
以及分类决策函数
称为线性可分支持向量机
假设在超平面w.x+b=0确定的情况下,|w.x+b|能够相对地表示点x距离超平面的远近,而w.x+b的符号与类标记y的符号是否一致能够表示分类是否正确,所以可用量y(w.x+b)来表示分类的正确性及确信度,这就是函数间隔,函数间隔说的更通俗点就是人为定义的一个间隔只是能用来表示所有点距离超平面的一个距离的定义罢了。你也可以用其他的一个定义来表示都是可以的。
函数间隔:
我们的目的就是要求得函数间隔的最小值,即
但是我们只有函数间隔是不够的,因为函数间隔是一种理论上的相对距离,当我们成比例的改变w和b的值的时候, 则也会变化变成原来的四倍。所以就有了后面的几何间隔的定义。

根据平面几何的知识:
其中||w||为w的二阶范数(范数是一个类似于模的表示长度的概念),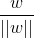
又由于 x0 是超平面上的点,满足 f(x0)=0 ,代入超平面的方程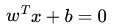
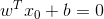
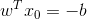
随即让此式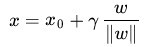
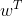
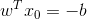
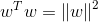
为了得到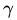
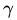
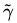
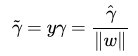
从上述函数间隔和几何间隔的定义可以看出:几何间隔就是函数间隔除以||w||,而且函数间隔y*(wx+b) = y*f(x)实际上就是|f(x)|,只是人为定义的一个间隔度量,而几何间隔|f(x)|/||w||才是直观上的点到超平面的距离。
最大间隔分离超平面
我们的目标就是如何求得一个几何间隔最大的分离超平面,具体的这个问题可以表示为下面的约束最优化问题:max
s.t
其中 为上面得到的最小几何距离。
用函数间隔表示的话即为:
max
s.t
其中为上面得到的最小函数距离。
事实上将w和b按比例改变为xw和xb以后,这时函数间隔为x,但是几何距离仍然为
,也就是说函数间隔大小的改变不会影响对目标函数的优化,对最终的结果是没有影响的,所以我们在这里可以取
=1,将
=1带入上面最优化问题,最大化
和最小化
是等价的,这样做的目的是为了方便后面的求导等求解过程。
所以最终我们的优化问题就变成了:
Min
s.t
最终就变成了一个凸优化问题。
最终优化得到的结果就是得到一个分隔超平面 w.x+b=0
对 =+1的正例点,支持向量在超平面 w.x+b=1上面
对 =-1的负例点,支持向量在超平面 w.x+b=-1上面
用对偶算法求解上述凸优化问题
先介绍一下什么是kkt条件,首先kkt是一个人名(大佬原名叫:Karush-Kuhn-Tucker ),之前我一直纳闷为啥叫kkt,
假设有一个优化问题:
Min f(x)
subject to: <=0 ,
=0.
上面的优化问题等价于:
Min
Subject to:
for i=1,2,3……N
因为=0,所以
的大小我们不关心,第一个条件是因为
有的为0有的小于等于0,对于
为0的项
的大小我们不关心,而对于
小于0的项我们希望
的大小为0,这样的话原目标函数的优化相当于没有发生改变。
进行对偶变化的目的是因为我们之前的优化问题中有条件为不等式,很难进行优化求解,但是变成对偶问题后只有等式了,这样的问题更容易进行求解, 这种单变量不等式没关系,不算在我说的不等式里面。
所以根据KKT条件原问题的对偶问题就变成了:
原问题的对偶问题是极大极小问题:max min L(w,b,)
极大极小的意思就是先求所有点中对超平面距离的最小的值,极大表示的意思是把这个最小值最大化。
先对w,b求极小值,再求对的极大化这个极小值。
L(w,b,)对w,b求偏导数并令其等于0.
得:
上述两个条件代入L(w,b,)等式中,得到所有点中离超平面的极小距离:
Min
对这个最小距离再求对的极大值。得到的就是最终我们所要求的解。
把这个求极大值转换成求极小值,就是变化下符号,所以最终我们的问题就变成了:
Min
s.t
最终求得结果后,可以反过来求解得到w和b的值。
至此,我们就通过对偶算法得到了SVM的解。(写了我一下午才到这,不容易啊,公式编辑很麻烦)
软间隔最大化
前面开头就有说,对于线性可分的情况是上面的求解方法,但是对于线性不可分的情况该咋整呢,
其实只需要把最开始的目标函数和约束条件做一点改动即可。变换成:
Min
s.t
关于软间隔后续的推导和前面所述硬间隔的推导大同小异,最终推导得到的最优化问题和前面的结果只有最后的条件有所改变,相当于对
做了一下约束。
Min
s.t
核函数
前面所说的软间隔支持向量机也只是在大体可线性可分,可能有个别干扰点的情况下使用,当数据是完全不可线性分割,很乱的时候,这个时候我们就需要用到核函数了,把数据从非线性状态变化成线性可分状态。
如下所示,把一个圆形可分的变化成一个线性可分的,利用圆的公式即可。








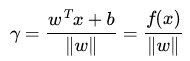















 3977
3977

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








