上一篇讲解了推荐算法的分类,这里电影推荐系统具体分析一下
第一步:建立用户电影矩阵模型
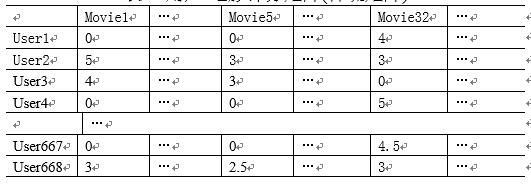
如表1所示,协同过滤算法的输入数据通常表示为一个m*n的用户评价矩阵Matrix,m是用户数,n是电影数,Matrix[ij]表示第i个用户对第j个电影的评价:
第二步:发现兴趣相似的用户
这一阶段,主要完成对目标用户最近邻居的查找,通过计算目标用户与其他用户之间的相似度,得到与目标用户最近的邻居集。度量用户间相似性:设N(u)为用户u喜欢的电影集合,N(v)为用户v喜欢的电影集合,将上一步中每行记录视为一个向量,那么u和v的相似度可通过以下进行计算:
(a)采用Jaccard公式:W_uv=(|N(u)∩N(v)|)/(|N(u)∪N(v)|)
(b)余弦相似度计算:W_uv=(|N(u)∩N(v)|)/(√|N(u)||N(v)|)
这里选择余弦公式进行相似度度量计算,假设目前共有4个用户(A、B、C、D),5部电影(a、b、c、d、e),用户与电影的关系如下图所示:
而这种方法的时间复杂度是O(|U|*|U|),所以非常耗时。而在上表中可以看到“用户-电影”表是一个稀疏矩阵,即很多时候N(u)^N(v)=0,如果换一下思路,可以首先计算N(u)^N(v)!=0的用户,然后再计算sqrt(N(u)*N(v))。为此可以首先建立“电影-用户”的倒排表,对每部电影都保存电影到用户的列表:
设稀疏矩阵C[u][v]=N(u)^N(v),在倒排索引中假设用户u和用户v同时属于倒排索引中K部电影对应的用户列表,就有C[u][v]=K。例如上图所示只有电影a中同时出来了用户有A和用户B,则在矩阵中赋值为1:
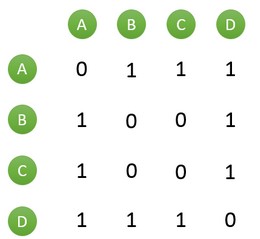

到此,用户间的相似度计算就得到了,可以很直观的找到与目标用户兴趣相似的用户。
第三步:产生推荐项目
需要从矩阵中找到与目标用户最相似的K个用户,用集合S(u,K)表示,将S中用户喜欢的电影全部提取出来,并除去u已经喜欢的电影。对每个候选电影i,用户对它的感兴趣的程度用以下公式计算:
(其中Rvi表示用户v对电影i的喜欢程度,此处举例全部为1,在电影评分时应该代入用户的评分)。
继续上面的例子,假设我们给A推荐电影,选取K=3,对用户A,电影c、e没有看过,因此可以将这两部电影推荐给用户A,根据UserCF算法用户A对物品c、e的兴趣分别计算p(A,c)和p(A,e):










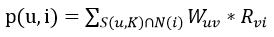
















 643
643

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








