STL源码分析之大顶堆

关于大顶堆和小顶堆这里就不再介绍了，这里通过STL再次回顾一下。

heap为了适应容器大小的不断变化，底层调用vector实现

关于heap的算法（这里是大顶堆）

 

push_heap（）算法

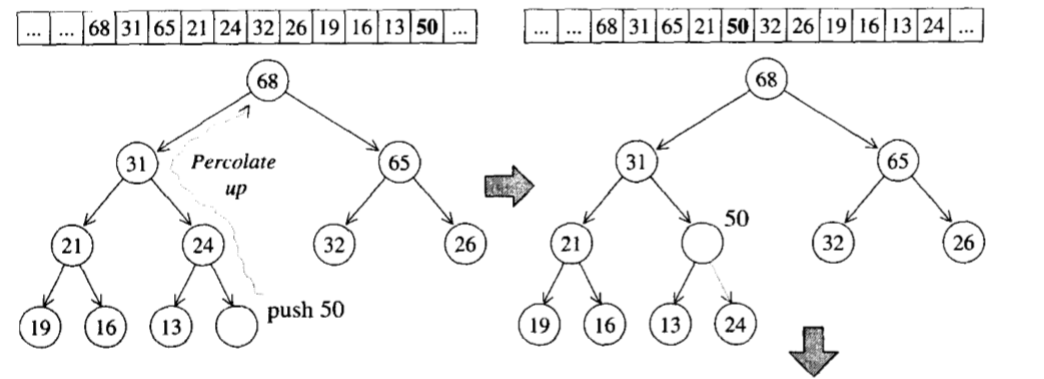
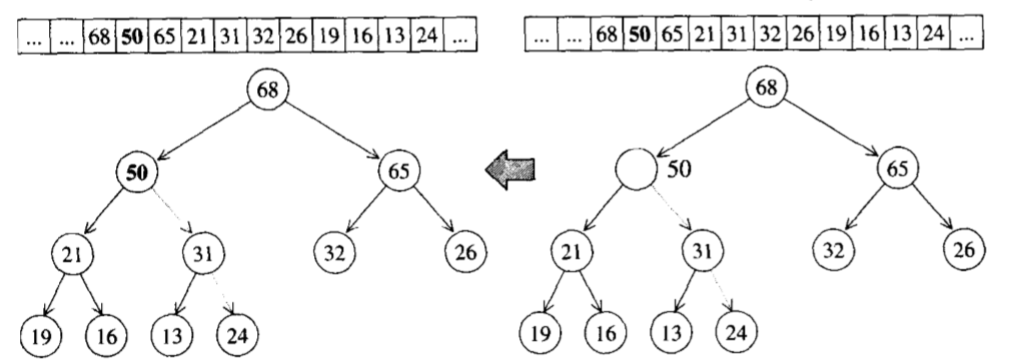
为了满足完全二叉树的条件，新加入的元素一定是放在最下一层作为叶节点，并填补在由左至右的第一个空格，即插在vector的end()处

 

 

我们通过上溯，将新节点与其父节点进行比较，如果键值比父节点的大，就对换位置，如此一直上溯，直到不需要对换或到了根节点为止。

以下即为push_heap的源码，两个迭代器表示heap底部容器（array或vector）的头尾，并且新的元素已经插入到底部容器的最尾端了。

template <classRandomAccessIterator>
inline voidpush_heap(RandomAccessIterator first, RandomAccessIterator last) {
  __push_heap_aux(first, last,distance_type(first), value_type(first));
}
 
template <class RandomAccessIterator,class Distance, class T>
inline void__push_heap_aux(RandomAccessIterator first,
                           RandomAccessIterator last, Distance*, T*) {
  __push_heap(first, Distance((last - first) -1), Distance(0),
              T(*(last - 1)));
}
 
//上面为了处理
//不管上面的内容，我们只要知道holeIndex就是插入的新节点在array/vector中的下标位置
template <classRandomAccessIterator, class Distance, class T>
void__push_heap(RandomAccessIterator first, Distance holeIndex,
                 Distance topIndex, T value) {
  Distance parent = (holeIndex - 1) / 2;                //新插入节点的父节点下标
    //循环的一个判断条件就是父节点是存在的 且 父节点的键值小于新节点的键值
  while (holeIndex > topIndex && *(first + parent)< value) {
    //这里的操作本应该是交换父节点和新节点的位置(或值)，因为value被一个变量指向了，所以这里只将新节点的值改为父节点的值，且将要处理的节点改为原来的父节点
    *(first + holeIndex) = *(first + parent);
holeIndex = parent;
//另求当前处理节点的父节点下标
    parent = (holeIndex - 1) / 2;
  }   
    //最后将这个指向新址的变量交给当前处理结束的节点
  *(first + holeIndex) = value;
}
 

 

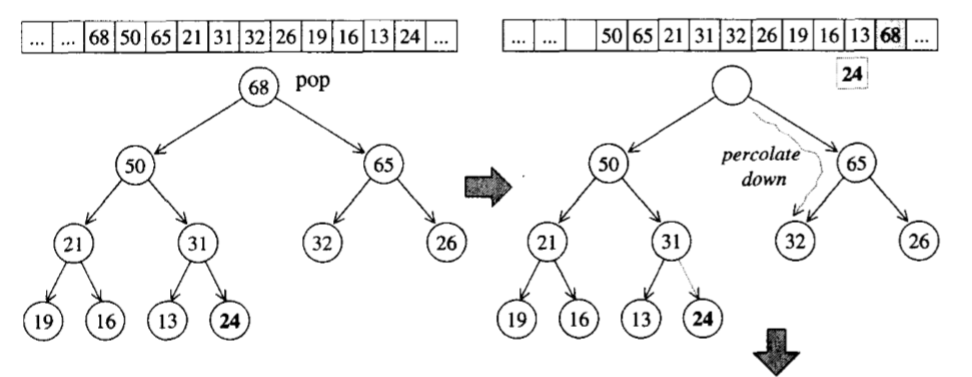
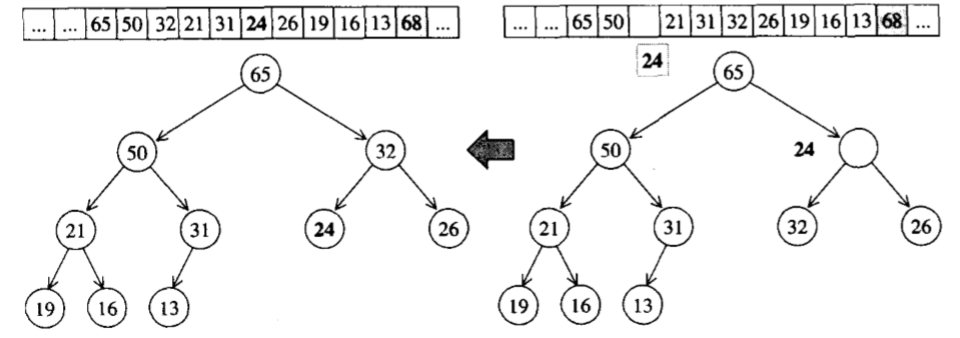
pop_heap（）算法

该操作取走根节点，即将整个堆最大的元素取走（其实是将此节点与整个堆的最后一个元素交换位置），然后进行下溯操作，调整整棵树

//这里我们只看核心部分
template <classRandomAccessIterator, class T, class Distance>
inline void__pop_heap(RandomAccessIterator first, RandomAccessIterator last,
                       RandomAccessIterator result, T value,Distance*) {
  *result = *first;
  __adjust_heap(first, Distance(0),Distance(last - first), value);
}
 
template <classRandomAccessIterator, class Distance, class T>
void__adjust_heap(RandomAccessIterator first, Distance holeIndex,
                   Distance len, T value) {
  Distance topIndex = holeIndex;            //当前大顶堆就是从根部开始调整
  Distance secondChild = 2 * holeIndex + 2;     //算出第二个儿子的下标位置。为什么要求第二个儿子的下标呢？因为可能这个节点只有1个儿子，可能都没有
  while (secondChild < len) {               //右子节点存在
    //如果左子节点的键值大于右子节点的键值
if (*(first +secondChild) < *(first + (secondChild - 1))) 
//那么可能要进行交换（有资格去跟父节点键值比较的）的就是左子
//因为是完全二叉树，底部容器是vector,所以求左子就是减一操作
      secondChild--;
    //令当前父节点的值直接等于该大的子节点
    //接下来直接修改要调整的节点为该子节点
    //原以为会令父子节点进行比较，可没有，是因为这个函数最后又调用了push_heap操作来调整这个节点。。。确实出乎我的意料了
    *(first + holeIndex) = *(first +secondChild);
    holeIndex = secondChild;
    secondChild = 2 * (secondChild + 1);
  }
    //如果没有右子，也能说明是走到最后了，因为是完全二叉树嘛
  if (secondChild == len) {
    *(first + holeIndex) = *(first +(secondChild - 1));
    holeIndex = secondChild - 1;
  }
  __push_heap(first, holeIndex, topIndex, value);
}

make_heap（）算法

即将一个无序的数组转化为heap形式

template <classRandomAccessIterator>
inline voidmake_heap(RandomAccessIterator first, RandomAccessIterator last) {
  __make_heap(first, last, value_type(first),distance_type(first));
}
 
template <class RandomAccessIterator,class Compare, class T, class Distance>
void__make_heap(RandomAccessIterator first, RandomAccessIterator last,
                 Compare comp, T*, Distance*) {
    //0或1个元素就不操作了
  if (last - first < 2) return;
  Distance len = last - first;
    //从有子节点的元素开始做向下调整
  Distance parent = (len - 2)/2;
   
  while (true) {
    __adjust_heap(first, parent, len, T(*(first+ parent)), comp);
if (parent == 0) return;
//调整完一个调整继续往前调整，直到根，然后就结束了
    parent--;
  }
}