leetcode刷题（126）——1289. 下降路径最小和 II

给你一个 n x n 整数矩阵 arr ，请你返回 非零偏移下降路径 数字和的最小值。

非零偏移下降路径 定义为：从 arr 数组中的每一行选择一个数字，且按顺序选出来的数字中，相邻数字不在原数组的同一列。

示例 1：

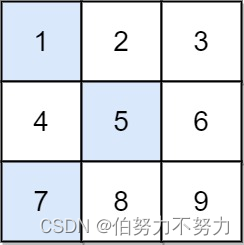
输入：arr = [[1,2,3],[4,5,6],[7,8,9]]
输出：13
解释：
所有非零偏移下降路径包括：
[1,5,9], [1,5,7], [1,6,7], [1,6,8],
[2,4,8], [2,4,9], [2,6,7], [2,6,8],
[3,4,8], [3,4,9], [3,5,7], [3,5,9]
下降路径中数字和最小的是 [1,5,7] ，所以答案是 13 。

示例 2：

输入：grid = [[7]]
输出：7

提示：

n == grid.length == grid[i].length
1 <= n <= 200
-99 <= grid[i][j] <= 99

动态规划

我们可以使用动态规划来解决这个问题。

我们用 f[i][j] 表示从数组 arr 的前 i 行分别选择一个数字，并且第 i 行选择的数字为 arr[i][j] 时，可以得到的路径数字和的最小值。f[i][j] 可以从第 i - 1 行除了 f[i - 1][j] 之外的任意状态转移而来，这样我们可以写出如下的状态转移方程：

f[i][j] = min(f[i - 1][j']) + arr[i][j]    其中 j != j'
f[0][j] = arr[0][j]

class Solution {
    public int minFallingPathSum(int[][] arr) {
        int n = arr.length;
        int[][] f = new int[n][n];
        // 初始化首行的路径和
        for (int i = 0; i < n; i++) f[0][i] = arr[0][i];
        // 从第一行进行转移
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < n; j++) {
                f[i][j] = Integer.MAX_VALUE;
                int val = arr[i][j];
                // 枚举上一行的每个列下标
                for (int p = 0; p < n; p++) {
                    // 只有列下标不同时，才能更新状态
                    if (j != p) {
                        f[i][j] = Math.min(f[i][j], f[i-1][p] + val);
                    }
                }
            }
        }
        // 在所有的 f[n - 1][i] 中取最小值
        int ans = Integer.MAX_VALUE;
        for (int i = 0; i < n; i++) {
            ans = Math.min(ans, f[n-1][i]);
        }
        return ans;
    }
}

这个动态规划的时间复杂度为 O(N^3)：我们需要使用三重循环分别枚举 i，j 和 j0。若使用 C++ 语言实现该算法，则可以恰好在规定时间内通过所有测试数据，但对于 Python 语言则无法通过。因此我们必须对该算法进行优化。

我们注意到，状态转移方程中的 min(f[i - 1][j’]) 在大多数情况下的值都是相同的。不妨记 f[i - 1][jmin] 是第 i - 1 行所有状态中的最小值，可以发现，在状态转移方程中：

如果 j != jmin，那么 f[i][j] 一定会从 f[i - 1][jmin] 转移而来，因为此时 min(f[i - 1][j’]) 这一项可以取到最小值；

如果 j == jmin，那么 f[i][j] 不能从 f[i - 1][jmin] 转移而来，那么我们需要选择第 i - 1 行所有状态中的次小值，使得 min(f[i - 1][j’]) 这一项取到最小值。

因此我们可以修改状态转移方程：

f[i][j] = f[i - 1][jmin[i - 1]] + arr[i][j]    其中 j != jmin[i - 1]
f[i][j] = f[i - 1][jnext[i - 1]] + arr[i][j]   其中 j == jmin[i - 1]
f[0][j] = arr[0][j]

其中 jmin[i - 1] 表示第 i - 1 行所有状态中最小值所在的位置，jnext[i - 1] 表示第 i - 1 行所有状态中次小值所在的位置，最小值和次小值可以相等。在计算完第 i - 1 行的所有状态之后，我们可以在 O(N)O(N) 的时间得到 jmin[i - 1] 和 jnext[i - 1]，这样在计算第 i 行的状态时，我们不需要枚举原先的 j0，时间复杂度从 O(N^2),
降低为 O(N)。因此总时间复杂度降低为 O(N^2)。

此外，我们还可以对空间复杂度进行优化。由于 f[i][j] 只会从 f[i - 1][jmin[i - 1]] 或 f[i - 1][jnext[i - 1]] 转移而来，那么我们并不用将第 i - 1 行的所有状态存储下来，而是可以浓缩成三个变量：

first_sum 表示这一行的最小值；

first_pos 表示这一行最小值对应的 jmin；

second_sum 表示这一行的次小值。

状态转移方程修改为：

f[i][j] = first_sum + arr[i][j]    其中 j != first_pos
f[i][j] = second_sum + arr[i][j]   其中 j == first_pos

通过这三个变量计算出第 i 行的所有状态之后，我们也不用将它们存储下来，同样可以浓缩成三个变量，为第 i + 1 行的动态规划提供转移基础。由于在计算第 i + 1 行的状态时，不需要第 i - 1 行的任何信息，因此第 i - 1 行浓缩成的三个变量此时可以被丢弃。这样以来，我们就将空间复杂度从 O(N^2) 降低至了 O(1)。

class Solution {
    public int minFallingPathSum(int[][] arr) {
        int n = arr.length;
        int first_sum = 0, first_pos = -1, second_sum = 0;
        for (int i = 0; i < n; ++i) {
            int fs = Integer.MAX_VALUE, fp = -1, ss = Integer.MAX_VALUE;
            for (int j = 0; j < n; ++j) {
                int cur_sum = (first_pos != j ? first_sum : second_sum) + arr[i][j];
                if (cur_sum < fs) {
                    ss = fs;
                    fs = cur_sum;
                    fp = j;
                }
                else if (cur_sum < ss) {
                    ss = cur_sum;
                }
            }
            first_sum = fs;
            first_pos = fp;
            second_sum = ss;
        }
        return first_sum;
    }
}