神经网络

最新推荐文章于 2024-04-22 15:51:44 发布

ZLin.Tang

最新推荐文章于 2024-04-22 15:51:44 发布

阅读量1.2k

点赞数 1

分类专栏： # 机器学习

本文链接：https://blog.csdn.net/u012344939/article/details/104385131

版权

机器学习专栏收录该内容

4 篇文章 0 订阅

订阅专栏

1.前言
1.当特征太多时，无论线性回归还是逻辑回归计算的负荷都会非常大。
2.使用非线性的多项式往往能够帮我们建立更好的分类模型。然而特征组合数量却非常惊人，例如：2500个特征，仅两两组合就有2500^2/2(近300万个)。普通逻辑回归不能有效处理这么多特征。
这时候我们需要神经网络。

2.神经网络简介（可直接参考：https://blog.csdn.net/illikang/article/details/82019945）
神经网络是一种模拟人脑的神经网络以期能够实现类人工智能的机器学习技术。在大脑中，神经网络是大量神经元相互连接并通过电脉冲来交流的一个网络。下面是一组神经元的示意图：

神经网络模型也建立在很多神经元之上，这些神经元也叫做激活单元。
输入——树突（Dendrite）
处理单元——神经核（Nucleus）
输出——轴突（Axon）

下图为一个三层神经网络：

Layer1：输入层——输入单元
Layer2：隐含层/中间层——隐含单元 /中间单元
Layer3：输出层——输出单元
$a_{i}^{(j)}$ :代表第j层的第i个激活单元。
$\theta ^{(j)}$ :代表从第j层映射到第j+1层时的权重的矩阵，行数为第j+1层的单元数量，列数为第j层单元数加一。
上图所示模型中，激活单元和输出分别表示为：
（1）
这里只是计算一个样本/一个训练实例的情况。而我们需要用所有样本来进行神经网络模型的训练。
像（1）式，每一层的a都是由上一层的所有x和x对应的权值决定的。每一层的输出变量都是下一层的输入变量。我们把这种从左到右的算法称为前向传播算法。我们可以把 $a_{1},a_{2},a_{3}$ 看成更为高级的特征看成更为高级的特征值，也就是 𝑥0,𝑥1,𝑥2,𝑥3的进化体，的进化体，并且它们是由 𝑥与决定的，因为是梯度下降所以 𝑎是变化的，并且得越来厉害，所以这些更高级的特征值远比仅将 𝑥次方厉害，也能更好的预测新数据。这就是神经网络相比于逻辑回归和线性的优势。

3.多类分类
当我们要训练一个神经网络来识别路人、汽车、摩托车和卡车，在输出层我们应该有四个值。例如第一个值为1或0用于预测是否是行人，第二个值用于判断是否是汽车...下面是该神经网络的可能结构示例：

神经网络算法的输出结果为下面四种可能情形之一：

4.代价函数
神经网络的分类分为二分类和多分类两种情况。

L：神经网络总层数
$S_{l}$ ：第 $l$ 层的单元数

逻辑回归中我们的代价函数为：
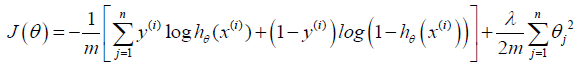   (2)
神经网络中，我们的 $h_{\theta}(x)$ 是一个维度为K的向量，代价函数为：
     (3)
对于每一个样本，我们会给出K个预测结果，然后在K个预测中选择可能性最高的一个，将其与y中实际数据进行比较。

5.求最优解
和逻辑回归一样，还是使用梯度下降方法来求解代价函数最优解。用梯度下降方法主要就是求代价函数的偏导数 $\frac{\alpha }{\alpha\theta^{(l)}}J(\theta)$ 。
先不考虑正则项，且只有一个样本，一个隐含层时：
$\begin{aligned} J(\theta )&= -[ylog(h_{\theta}(x))+(1-y)log(1-h_{\theta}(x))]\\ &=-[ylog(\frac{1}{1+e^{-\theta ^{T}x}})+(1-y)log(1-\frac{1}{1+e^{-\theta ^{T}x}})]\\ &=ylog(1+e^{-\theta ^{T}(x))})+(1-y)log(1+e^{\theta ^{T}(x))}) \end{aligned}$ (4)
对 $\theta$ 求偏导得：
$\begin{aligned} \frac{\alpha }{\alpha \theta }J(\theta )&=(\frac{1}{1+e^{-\theta ^{T}x}}-y)x\\ &=(h_{\theta }(x)-y)x \end{aligned}$ (5)
但神经网络往往都有多个隐含层，如何对多个隐含层 $\theta ^{(l)}$ 求偏导呢？

前向传播算法
前面我们计算神经网路的预测结果时采用了前向传播方法，我们从第一层开始正向一层一层进行计算，直到最后一层。假设我们只有一个训练实例 $(x^{(1)},y^{(1)})$ ，我们的神经网络是一个四层神经网络。其中 $K=2$ （类别数）， $S_{L}=1$ （最后一层单元数）， $L=4$ ：

即：

$h_{\theta }(x) = g(\theta ^{(3)}g(\theta ^{(2)}g(\theta ^{(1)}x)))$ （6）
带入代价函数：
$J(\theta )&= -[ylog(g(\theta ^{(3)}g(\theta ^{(2)}g(\theta ^{(1)}x))))+(1-y)log(1-g(\theta ^{(3)}g(\theta ^{(2)}g(\theta ^{(1)}x))))]$ （7）
后向传播算法
$J(\theta )&= -[ylog(g(\theta ^{(3)}g(\theta ^{(2)}g(\theta ^{(1)}x))))+(1-y)log(1-g(\theta ^{(3)}g(\theta ^{(2)}g(\theta ^{(1)}x))))]$

$\frac{\alpha }{\alpha \theta ^{(1)}}J(\theta ) = (h_{\theta }(x)-y)*\theta ^{(3)}*g(\theta ^{(2)}g(\theta ^{(1)}x))*(1-g(\theta ^{(2)}g(\theta ^{(1)}x)))*\theta ^{(2)}*g(\theta ^{(1)}x)(1-g(\theta ^{(1)}x))*x$

$\frac{\alpha }{\alpha \theta ^{(2)}}J(\theta )=(h_{\theta }(x)-y)*\theta ^{(3)}*g(\theta ^{(2)}g(\theta ^{(1)}x))*(1-g(\theta ^{(2)}g(\theta ^{(1)}x)))*g(\theta ^{(1)}x)$

$\frac{\alpha }{\alpha \theta ^{(3)}}J(\theta ) = (h_{\theta }(x)-y)*g(\theta ^{(2)}g(\theta ^{(1)}x))$

仔细看看其实这些式子是有关系的：
令 $\delta ^{(4)} =h_{\theta }(x) - y$ ，则:

$\frac{\alpha }{\alpha \theta ^{(3)}}J(\theta ) = \delta ^{(4)}a ^{(3)}$
令
$\begin{aligned} \delta ^{(3) }&=(h_{\theta }(x)-y)*\theta ^{(3)}*g(\theta ^{(2)}g(\theta ^{(1)}x))*(1-g(\theta ^{(2)}g(\theta ^{(1)}x)))\\ &=\delta ^{(4)}\theta ^{(3)}g'(z^{(3)}) \end{aligned}$
则：
$\frac{\alpha }{\alpha \theta ^{(2)}}J(\theta ) = \delta ^{(3)}a ^{(2)}$
令
$\begin{aligned} \delta ^{(2) }&=(h_{\theta }(x)-y)*\theta ^{(3)}*g(\theta ^{(2)}g(\theta ^{(1)}x))*(1-g(\theta ^{(2)}g(\theta ^{(1)}x)))*\theta ^{(2)}*g(\theta ^{(1)}x)(1-g(\theta ^{(1)}x))\\ &=\delta ^{(3)}\theta ^{(2)}g'(z^{(2)}) \end{aligned}$

$\frac{\alpha }{\alpha \theta ^{(1)}}J(\theta ) = \delta ^{(2)}a ^{(1)}$
我们把 $\delta ^{(l)}$ 看成 $l$ 层的误差，然后由后一层误差算出前一层的误差，第一层是输入变量不存在误差，偏导数也是由后往前计算。这种方法我们称其为后向传播算法。
如果直接用前向算法计算偏导数，则会存在很多重复的计算。
$\frac{\alpha }{\alpha \theta ^{(1)}}J(\theta ) = (h_{\theta }(x)-y)*\theta ^{(3)}*g(\theta ^{(2)}g(\theta ^{(1)}x))*(1-g(\theta ^{(2)}g(\theta ^{(1)}x)))*\theta ^{(2)}*g(\theta ^{(1)}x)(1-g(\theta ^{(1)}x))*x$

$\frac{\alpha }{\alpha \theta ^{(2)}}J(\theta )=(h_{\theta }(x)-y)*\theta ^{(3)}*g(\theta ^{(2)}g(\theta ^{(1)}x))*(1-g(\theta ^{(2)}g(\theta ^{(1)}x)))*g(\theta ^{(1)}x)$

$\frac{\alpha }{\alpha \theta ^{(3)}}J(\theta ) = (h_{\theta }(x)-y)*g(\theta ^{(2)}g(\theta ^{(1)}x))$
先算 $\frac{\alpha }{\alpha \theta ^{(1)}}J(\theta )$ 再算 $\frac{\alpha }{\alpha \theta ^{(2)}}J(\theta )$ 再算 $\frac{\alpha }{\alpha \theta ^{(3)}}J(\theta )$ ，可以看到很多都重复计算了。
总结神经网络求最优解步骤
step1：随机初始化参数 $\theta$ ；
step2：通过前向算法计算出每一层的激活单元 $a^{(l)}$ ；
step3：计算最后一层的误差 $\delta ^{(L)}=h_{\theta }(x)-y$ ，利用该误差运用反向传播法计算直至第二层的所有误差 $\delta ^{(l)}$ ；
step4：计算偏导数 $\frac{\alpha }{\alpha \theta ^{(l)}}J(\theta ) = \delta ^{(l+1)}a ^{(l)}$ ；
step5：计算梯度 $D^{(l)}=\frac{1}{m}\frac{\alpha }{\alpha \theta ^{(l)}}J(\theta )+\lambda \theta ^{(l)}$ （注意：计算时偏置项参数不参与正则化）；
step6：更新参数 $\theta ^{(l)}:=\theta ^{(l)} - \alpha D^{(l)}$ ；
step7：不断迭代step2-6更新参数直至达到收敛条件。

6.随机初始化参数
逻辑回归中，参数都初始化为0，但这种方法对于神经网络行不通。如果我们令所有的初始参数都为0，这意味着我们的第二层的多有激活单元都会有一样的值，同理，全部初始化为同一个不为0的数结果也一样。我们通常初始化参数为正负 $\epsilon$ 之间的随机值。其中 $\epsilon$ 的取值通常为：
$\epsilon =\frac{\sqrt{6}}{\sqrt{L_{in}+L_{out}}}$
$L_{in}$ 、 $L_{out}$ 分别表示该对应的上下层的单元数。

7.梯度检验
当我们对一个复杂的模型使用梯度下降时，可能会存在一些不容易察觉的错误，意味着，虽然代价看上去在不断减小，但最终的结果并不是最优解，为解决这样的问题，我们可以采取一种叫梯度的数值检验的方法。在一个特定的 $\theta_{1}$ ，我们计算出 $J(\theta_{1} -\epsilon )$ 、 $J(\theta_{1} +\epsilon )$ ， $\epsilon$ 是个很小的值，通常取0.001

在 $\theta_{1}$ 处的偏导数近似为：
$\frac{\alpha }{\alpha \theta _{1}} = \frac{J(\theta _{1}+\epsilon _{1},\theta _{2},,,\theta _{n})-J(\theta _{1}-\epsilon _{1},\theta _{2},,,\theta _{n})}{2\epsilon _{1}}$
依次计算出所有的偏导数，然后和通过反向算法计算出的偏导数比较，正常情况两者差异甚小。

8.代码实现（python）

ZLin.Tang

关注

1
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
神经网络

1.前言 1.当特征太多时，无论线性回归还是逻辑回归计算的负荷都会非常大。 2.使用非线性的多项式往往能够帮我们建立更好的分类模型。然而特征组合数量却非常惊人，例如：2500个特征，仅两两组合就有2500^2/2(近300万个)。普通逻辑回归不能有效处理这么多特征。这时候我们需要神经网络。2.神经网络简介（可直接参考：https://blog.csd...
复制链接

扫一扫