对称加密之流密码RC4

对称流式加密RC4算法

在前面文章中介绍了两种对称分组加密算法DES和AES，在本文将介绍另外一种对称加密方式——对称流式加密（流密码），和对称分组加密一样，流密码也是采用单密钥，但与分组加密不同，流式加密不是对明文分组后对每个分组进行同样的加密操作，而是根据密钥产生一个伪随机密码流，连续不断地对明文字节流进行处理，产生密文输出流。

一. 随机数和伪随机数介绍

在给多样的网络安全应用程序加密的过程中，随机数起了一个很重要的作用。而根据密码学原理，校验随机数的随机性有以下三个标准：

1. 统计学伪随机性。统计学伪随机性指的是在给定的随机比特流样本中，1和0出现的频率必须大致相同；
2. 密码学安全的伪随机性。即给定随机样本的一部分和随机算法，不能有效的演算出随机样本的剩余部分；
3. 真随机性。其定义为随机样本不可重现。实际上只要给定边界条件，真随机数并不存在，可是如果产生一个真随机数样本的边界条件十分复杂且难以捕捉（比如计算机系统的瞬间系统时钟），可以认为用这个方法演算出来了真随机数。

相应的，随机数也分为以下三类：

1. 伪随机数，满足上述第一个标准；
2. 密码学安全的伪随机数，满足上述第1、2标准；
3. 真随机数，同时满足上述三个标准。

实际上，用通俗易懂的方式解释真随机数（Random Number）和伪随机数（Pseudo Random Number）的本质区别就是，真随机数采用一个完全随机、不可复制的随机源作为输入端（熵源），比如计算机瞬时的电气特性、鼠标移动的坐标、计算机瞬间的系统时钟等，根据这个真随机输入端产生二进制数输出，这个过程是不可复现的（除非保留了这个熵源和输出产生规则）。而伪随机数采用一个事先约定的不变值作为输入端，这个不变值称为种子（在加密算法中即为密钥），按照确定的算法来产生一系列的被种子所决定的输出流，这个输出流在同时掌握种子和确定性算法的情况下可以被复现获得，而在没有种子的情况下，这个输出流“看起来”是随机的（Pseudo-randomness）。

图 1.1 真随机数发生器

图 1.2 伪随机数发生器

二. 流密码

在之前文章中讲到的分组密码每次使用相同的密钥按照相同的流程处理一个输入元素分组，并为每个输入分组产生一个输出分组。而流密码加密过程则是使用初始密钥产生一个伪随机的密码流，连续地处理输入元素序列（通常是用密码流和输入序列做异或运算），产生对应的连续输出序列（密文）。而解密过程则是采用和加密过程同样的伪随机流产生器算法对初始密钥产生一个相同的伪随机密码流，与密文序列做异或运算，得到明文序列。

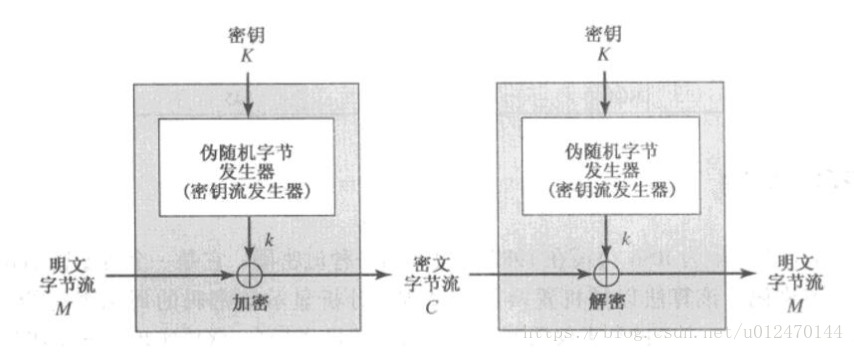
图 2.1 流密码结构

伪随机字节产生器（PRNG）以初始密钥作为种子，输出不断重复的周期密钥流，这个重复的周期越长，密码破解就越困难。而PRNG采用的伪随机函数（PRF）产生的周期内密码流越“随机”，对应输出的密文流也就越随机化。因此 初始密钥的长度和PRF的合理设计是流密码加密安全性的关键。对于密钥长度，分组密码中考虑的因素在这里同样适用，在当前的科技水平下，流密码至少需要128位长度的密钥。

三. RC4算法

RC4算法是Ron Rivest在1987年设计的流密码，密钥长度可变，使用面向字节的操作。有分析指出，RC4算法的密码流周期完全可能大于