LBP(局部二进制模式)

最新推荐文章于 2024-05-19 15:17:35 发布

u012507022

最新推荐文章于 2024-05-19 15:17:35 发布

阅读量1.8w

点赞数 5

分类专栏： Image processing 文章标签：图像处理计算机视觉

本文链接：https://blog.csdn.net/u012507022/article/details/51602916

版权

Image processing 专栏收录该内容

15 篇文章 12 订阅

订阅专栏

LBP(Local Binary Patterns ,局部二进制模式)是一种理论简单、计算高效的非参数局部纹理特征描述子。由于其具有较高的特征鉴别力和较低的计算复杂度，近期获得了越来越多的关注，在图像分析、计算机视觉和模式识别领域得到了广泛的应用，尤其是在纹理分类和人脸识别两个经典的模式识别问题中，LBP方法得到充分的研究和发展。

局部二进制模式(LBP)方法最早由芬兰Oulu大学提出，目前该方法已经成为纹理分类和人脸识别领域主要的特征提取方法之一，并在图像处理和计算机视觉领域受到越来越多的关注。

LBP方法存在如下显著优势:

1)计算复杂度低;

2)无需训练学习;

3)光照不变性;

4)易于工程实现

图 0.LBP算子抗单调灰度变换

正是因为如此，该方法已被成功应用于以纹理分类和人脸识别为代表的诸多图像处理和计算机视觉领域，包括工业检测、遥感图像分析、动态纹理识别、基于内容的图像检索、医学图像处理、人脸检测、场景分类、运动分析和环境建模等等，出现了大量 LBP 改进方法。

一、原始LBP描述子
最原始的LBP算子定义在某中心像素及其周围大小为3 × 3 的矩形邻域系统上，如图1所示，将中心像素的每个邻域像素值以该中心像素的灰度值为阈值进行二值量化，大于或等于中心像素的像素值则编码为1，小于则编码为0，以此形成一个局部二进制模式。将该二进制模式以x正轴方向为起点按照逆时针方向进行串联得到一串二进制数字，并用该二进制数对应的十进制数字来唯一地标识该中心像素点图像中的每个像素都可以计算得到一个局部二进制模式。

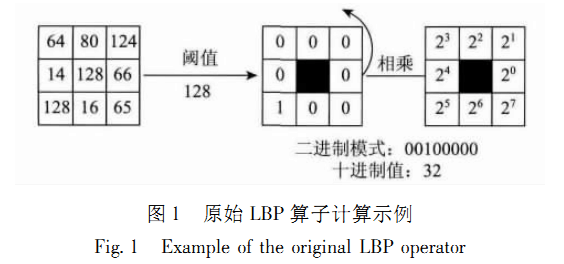
定义在大小为3×3的矩形邻域系统上的LBP模式的应用受到严重制约，主要原因在于:

1)3×3的邻域系统过于局部，无法捕获大尺度的纹理结构特征;

2)矩形邻域系统不宜于旋转不变特征的设计

针对这些不足，Ojala等人提出采用圆形邻域系统(如图2所示)来计算LBP模式，并通过采用不同大小的圆形邻域系统(如图3所示)将LBP扩展到多尺度上,没有位于图像像素中心位置的邻域像素采用双线性差值方式获得。数学上，如图2所示，给定图像中位于(i,j)的某像素Xc及以该像素为中心的半径为r的圆周上等角间距均匀分布的p个邻域像素。

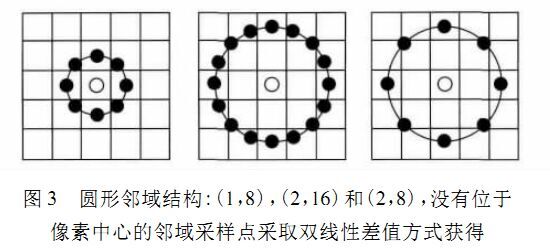
基于p个邻接采样点的LBP模式总共有2^p种,用于表示整幅纹理图像的LBP直方图矢量的维数为2^p。通过改变参数对(r，p)的值，可以获得不同尺度上的LBP模式。Ojala等人经过实验比较，在特征鉴别力和特征维数之间做一个折中，建议(r，p) 选取为(1,8)、(2,16)、(3,24)、(r,8r)。
给定一幅大小为M×N的纹理图像Img，常用的方法是通过统计纹理图像中所有像素对应的LBP模式出现的频率直方图H，作为该纹理图像的全局特征描述。

缺点：

1）LBPr,p不具有旋转不变性，而要提高一个特征描述子的实用性，需要增强对图像旋转变化的鲁棒性，

2）另一个严重劣势在于，全局LBP直方图矢量的维数随着p的增加而成指数增长，很快就受到计算和存储的限制。为了解决这两个问题，Ojala等人继续进行了改进，创新性地提出了旋转不变(rotation invariant)LBP模式与均匀(uniform)LBP模式，以及两者的结合得旋转不变均匀LBP模式。

二、旋转不变LBP描述子

当图像旋转时，某中心像素周围的圆形邻接像素也会发生变化，进而引起LBP模式的改变(全为0或者全为1的LBP模式除外) 。为了减轻图像旋转带来的影响，Ojala等人提出一种旋转不变算子。如图1中的二进制模式00100000 逆时针移动3次，得一个新的LBP模式00000001，旋转不变LBP描述算子中,00100000和00000001被认为是同一种模式。相比原始LBPr,p描述子，旋转不变描述子的直方图特征维数明显降低。
但是随着尺度的增加仍然很高，限制了其应用，因此研究者仅仅测试了旋转不变LBP(1,8)描述子的旋转不变纹理分类性能。研究表明旋转不变LBP(1,8)描述子的旋转不变纹理分类性能较差，主要原因是单一尺度描述能力不足，且角度空间采样较稀疏。

三、均匀LBP描述子
Ojala等人注意到在所有同一尺度下的原始LBP模式LBPr,p中,有些模式出现的频率显著高于其他模式,于是有理由认为出现概率高的模式包含更多的局部纹理信息，从某种意义上来说它们反映了纹理图像中的基本局部模式。因此Ojala 等人建议采用所有LBPr,p模式的一些子集来描述纹理图像特征，提出所谓的均匀LBP算子，为后续研究者所广泛采用。
该方法按照一定的准则将原始LBPr,p模式划分为均匀模式和非均匀模式两大类。一个LBP模式称为均匀模式，是指其U值不大于2。U值表示LBP模式中在圆周上相邻的两个二元值的0/1(或1/0)转移次数。

举例来说,LBPr,p模式00000000和01110000均为均匀模式，因为它们的0/1(或1/0)转移次数分别为0和2，即U(00000000) = 0，U(01110000)=2，而模式01100101为非均匀模式因为 U( 01100101)=5。U值反应了局部纹理结构的一种均匀性度量，U值越大表示结构趋向于不均匀，变化频率较高，U 值越小则反之，而图像中很多信息集中在低频，因此有理由认为均匀模式要比非均匀模式多，图4给出了几种典型的均匀模式及其表示的结构特征，对于参数(r,p)，共有均匀模式成p(p-1)+2种，而其余所有的非均匀模式将被统计一种，故均匀LBP描述子的特征的直方图维数为p(p-1)+3。均匀LBP描述子的特征的直方图维数较原始 LBP 描述子和旋转不变LBP描述子有了显著降低，使其扩展到多尺度上成为可能。但是在很多标准的均匀LBP描述子应用中,通常局限于3个尺度。

图4.几种典型的均匀模式

四、旋转不变均匀LBP描述子
为了进一步提高LBP特征描述子的旋转不变性能，并进一步降低其特征维数，在原始LBP描述子、旋转不变LBP描述子、均匀LBP描述子的基础上， Ojala等人提出旋转不变均匀LBP描述子。在旋转不变LBP描述子的基础上，将旋转不变LBP 模式进一步分为均匀旋转不变模式和非均匀模式。旋转不变均匀模式仅p+1类,所有非均匀模式归为1类，按照这种方式,最后用于表示整幅纹理图像的旋转不变LBP描述子的直方图矢量特征仅 p + 2 维，显著低于之前讨论的 3 种 LBP 描述子，Ojala 等人通过大量旋转不变和光照不变纹理分类实验，得出旋转不变均匀LBP描述子不仅具有最低的特征维数，在保持满意的特征鉴别力的同时具有较好的旋转不变性能和灰度尺度不变性能，因此该描述子得到后续研究者的青睐。在标准的 LBP 描述子应用中，通常采用旋转不变均匀LBP 描述子。

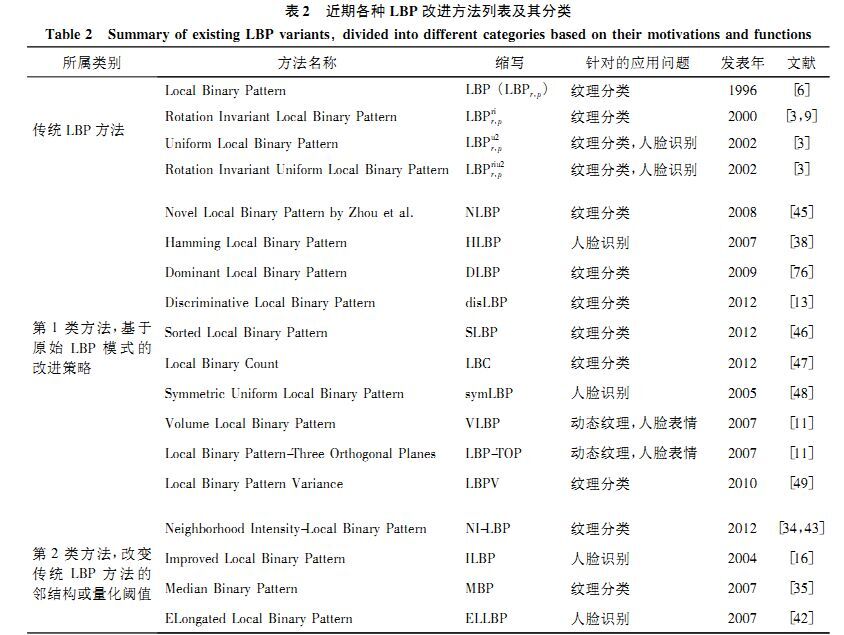
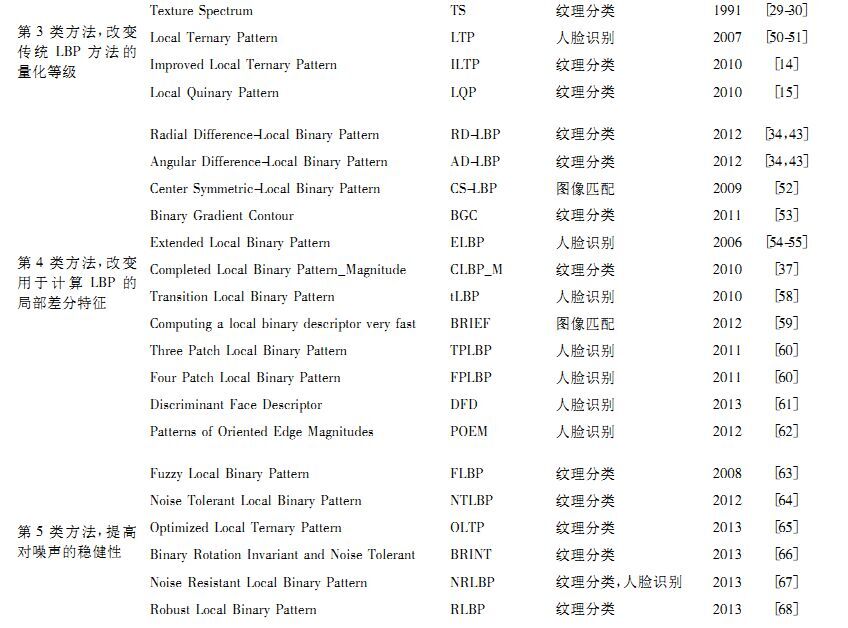
五、LBP改进算法