快速排序算法

最新推荐文章于 2024-07-18 22:30:07 发布

KVMK

最新推荐文章于 2024-07-18 22:30:07 发布

阅读量701

点赞数

分类专栏：算法文章标签： Java 算法排序算法快速排序

本文链接：https://blog.csdn.net/u012727078/article/details/16578403

版权

算法专栏收录该内容

9 篇文章 0 订阅

订阅专栏

快速排序是由東尼·霍爾所發展的一種排序算法。在平均狀況下，排序 n 個項目要Ο(n log n)次比較。在最壞狀況下則需要Ο(n²)次比較，但這種狀況並不常見。事實上，快速排序通常明顯比其他Ο(n log n) 演算法更快，因為它的內部循环（inner loop）可以在大部分的架構上很有效率地被實作出來。

快速排序使用分治法（Divide and conquer）策略來把一個序列（list）分為兩個子序列（sub-lists）。

步驟為：

從數列中挑出一個元素，稱為 "基準"（pivot），
重新排序數列，所有元素比基準值小的擺放在基準前面，所有元素比基準值大的擺在基準的後面（相同的數可以到任一邊）。在這個分割結束之後，該基準就處於數列的中間位置。這個稱為分割（partition）操作。
递归地（recursive）把小於基准值元素的子數列和大於基准值元素的子數列排序。

遞迴的最底部情形，是數列的大小是零或一，也就是永遠都已經被排序好了。雖然一直遞迴下去，但是這個演算法總會結束，因為在每次的迭代（iteration）中，它至少會把一個元素擺到它最後的位置去。

最差時間複雜度	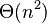$\Theta(n^2)$
最優時間複雜度	$\Theta(n\log n)$
平均時間複雜度	$\Theta(n\log n)$
最差空間複雜度	根據實現的方式不同而不同

算法稳定性：不稳定

package com.kvmk.sort;

public class QuickSort {

public static void quickSort(int[] originalArr, int i , int j) {
        int pivot = originalArr[i];
        int oi = i;
        int oj = j;
        if (oi == oj) {
            return;
        }
        
        while (i < j) {
            // scan from j, if find less than pivot, swap
            while (i < j) {
                if (originalArr[j] < pivot) {
                    swap(originalArr, i, j);
                    break;
                }
                j--;
            }
            // scan from i, if find great than pivot, swap
            while (i < j) {
                if (originalArr[i]> pivot) {
                    swap(originalArr, i, j);
                    break;
                }
                i++;
            }
        }
        quickSort(originalArr,oi,i);
        if (i+1 < oj) {
            quickSort(originalArr,i+1,oj);    
        }
    }
    
    public static void swap(int[] arr, int i, int j) {
        int temp;
        temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    
    /**
     * @param args
     */
    public static void main(String[] args) {
        int[] originalArr = new int[] {1,9,90,4,40,30,5,9,8,12};
        quickSort(originalArr,0,originalArr.length-1);
        for(int item : originalArr) {
            System.out.println(item);
        }
    }

}