注:本文中所有公式和思路来自于邹博先生的《机器学习升级版》,我只是为了加深记忆和理解写的本文。
概率图模型分为贝叶斯网络和马尔科夫网络,贝叶斯网络是有向图模型,马尔科夫网络是无向图模型(顺序演变),贝叶斯网络这一块知识我个人是学习了好多遍,看完之后虽说是明白但是却觉得很虚,我们耳熟能详的HMM、LDA都属于贝叶斯网络(有向图模型),条件随机场是马尔科夫网络(无向图模型)中的算法,后续也会介绍这两种重要的模型。
贝叶斯网络:
我其实挺不喜欢说一些概念性的东西,所以贝叶斯网络的概念我还是用大白话表述吧:现在有一个模型系统,其中有很多的随机变量(特征),我们根据这些随机变量之间是否条件独立绘制有向图,从而形成贝叶斯网。如果有现成的领域知识(例如:抽烟很可能得支气管炎),尽量使用领域知识建立模型,当然我们可以用计算的方式来辅助计算变量之间是否条件独立。
一般来说随机变量是指可观测的变量、隐变量、未知参数等等,两个节点之间用箭头表示因果关系,两节点之间就会产生一个概率值。
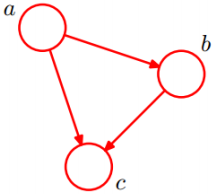
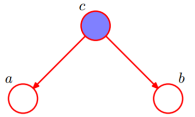
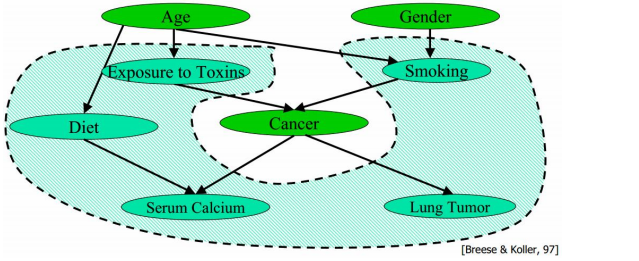
现在有一个简单地贝叶斯网络图:
用公式可以如下表示:
公式和上边的概率图所表达的信息量是一样的。
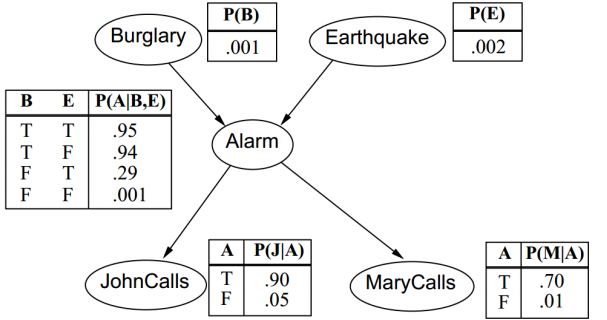
接下来我们举一个比较直观的例子来说明贝叶斯网络:
简单描述一下这个图:盗窃(Burglary)和地震(Earthquake)会引发警报(Alarm),警报响后会导致John打电话和Mary打电话通知,傍边的概率对应着随机变量之间的条件概率。
我们可以计算一下随机变量的联合概率:
接下来要讲述一下通过贝叶斯网络判断条件独立:
tail-to-tail
根据概率图模型:
P(a,b,c) = P(c)*P(a|c)*P(b|c)
P(a,b,c)/P(c)=P(a|c)*P(b|c)
P(a,b|c)=P(a|c)*P(b|c)
所以看得出来在上边这种tail-to-tail模型在给定c的条件下a、b就是独立的。
head-to-tail
根据概率图模型:
P(a,b,c) = P(a)*P(c|a)*P(b|c)
P(a,b,c)/P(c) = P(a)*P(c|a)*P(b|c)/P(c)
P(a,b|c) = P(a)*P(b|c)/P(c)
P(a,b|c) = P(a)*P(b)
很明显,在上边这种head-to-tail模型下,给定c的条件下a、b就是独立的
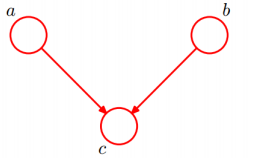
head-to-head
根据概率图模型:
P(a,b,c) = P(a)*P(b)*P(c|a,b)
可以看得出,在head-to-head这种模型下,给定c之后,a、b被阻断,a、b就是条件独立的。
最后跟大家介绍一下马尔科夫毯(Markov Blanket):
一个结点的Markov Blanket是一个集合,在这个集合中的结点给定的前提下,该结点跟给其他所有结点条件独立。
一个结点的Markov Blanket是他的parent、children、spouses(孩子的其他父结点),给张图说明Markov Blanket:
贝叶斯网络的用途:
a: 诊断: P(病因|病状)
b: 预测: P(病状|病因)
c: 分类: MaxclassP(类别|数据)
通过给定的样本数据,建立贝叶斯网络的拓扑结构和结点的条件概率分布参数,往往需要借鉴先验知识和极大似然估计来完成。
在给定贝叶斯网络的拓扑结构和结点的条件概率的分布后,可以使用该网络,计算未知数据的条件概率和后验概率,从而达到分类、预测、诊断的目的。
到此,贝叶斯网络介绍完了,欢迎大家批评指正!








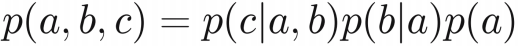
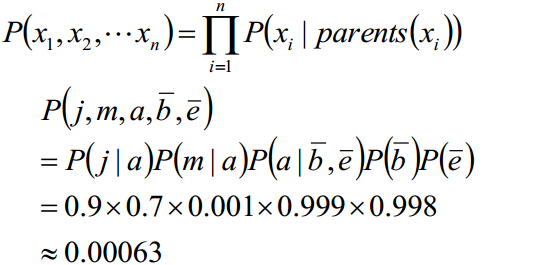
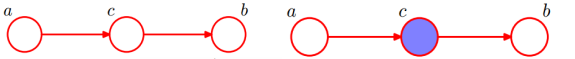
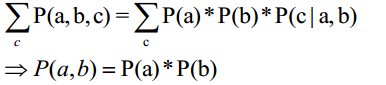














 7144
7144

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








