注:本文中所有公式和思路来自于邹博先生的《机器学习升级版》,我只是为了加深记忆和理解写的本文。
上一篇文章中,介绍了沿着梯度下降的方法,其实我们不一定非要沿着梯度下降的。
我们首先做个思考,我们都知道二阶导数反映了函数的凸凹性,二阶导数反映了一阶导数变化的大小,那么在搜索中我们可以考虑使用二阶导来进行修正:
我们可以将f(x)在xk处Taylor展开:
扔掉高阶导信息:
最终的得到迭代公式:
这就是牛顿法。
牛顿法总结:
(1): 经典牛顿法虽然具有二次收敛性,但是要求初始点尽量接近极小值点,否则可能不会收敛。
(2): 计算过程中需要计算目标函数的二阶导数的逆,时间复杂度高。
(3): 目标函数的Hessian矩阵无法确保正定,会导致算法产生的方向不能保证是f(x)的下降方向。
既然求Hessian矩阵的逆影响算法效率,方向上也可能出问题,因此可以用近似的矩阵代替hessian矩阵,接下来就介绍两种拟牛顿方法:DFP、BFGS
DFP
记函数f(θ)的梯度为g(θ),二阶导数为H(θ),那么在θi做Tarlor展开:
上边是Tarlor展开后的推导,其中第三行是做了对θ求导的操作,第四行我们将θ取θi-1,倒第二行我们做了简单的符号定义。
其中Ci是个Hessian矩阵,我们使用简单的向量来替换:
进一步推导代换:
接下来我们进行系数对比来解:
最终我们可以求出Ci:
当然了,我们可以通过交换参数g和θ,的到另外一个公式,DFP的迭代公式是:
交换参数:
BFGS
我们DFP中求的Ci其实是Hessian的逆矩阵,而BFGS则是直接求了Hissian矩阵。
首先先介绍一个公式Sherman-Morrison公式:若A是n阶可逆矩阵,u、v为n维列向量,若≠-1,则:
那么根据上边我们交换参数g和θ得到的公式:
使用两次Sherman-Morrison公式即可得到:
这个公式我们直接拿来写代码就好了。
L-BFGS
BFGS需要存储n*n的方阵Ck用来近似Hessain矩阵的逆矩阵,而L-BFGS仅需存储m个:
用于近似Ck即可。
L-BFGS的空间复杂度维O(mn),若将m看作常数,那么空间复杂度就是线性的,特别适合变量非常多的优化问题中。
到此所有的下降算法都讲完了,其中SGD很重要,是和在线学习,拟牛顿可以给出更好的下降方向。









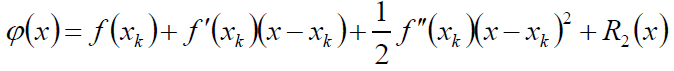
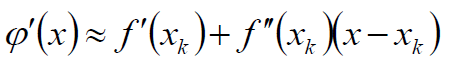
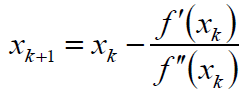


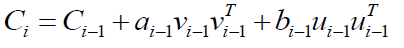
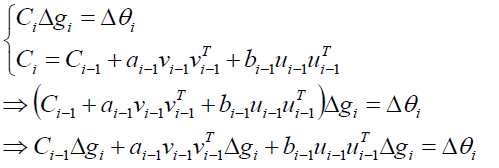
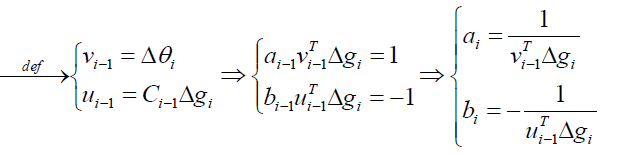
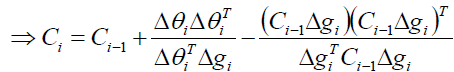
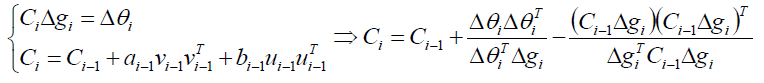

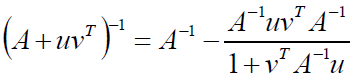
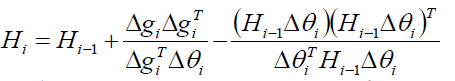

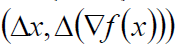














 1009
1009











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








