深度探索：机器学习中的拟牛顿法原理及其应用

目录

1. 引言与背景

2. 拟牛顿定理

3. 算法原理

4. 算法实现

5. 优缺点分析

优点：

缺点：

6. 案例应用

7. 对比与其他算法

8. 结论与展望

---

1. 引言与背景

在机器学习领域，优化算法是模型训练的核心环节，其性能直接影响模型的收敛速度、精度以及泛化能力。在众多优化算法中，拟牛顿法凭借其结合了牛顿法的快速局部收敛性与梯度下降法的简单高效，成为解决大规模非线性优化问题的重要工具。本文将围绕拟牛顿法展开详尽讨论，包括其理论基础、算法原理、实现细节、优缺点分析、实际应用案例、与其他算法的对比，以及对未来发展态势的展望。

2. 拟牛顿定理

拟牛顿法的核心思想是构造一个近似的海森矩阵（Hessian matrix），用以替代牛顿法中真实的海森矩阵，以降低计算复杂度并避免直接求逆。这一思想源自牛顿-拉普森迭代公式：

其中， 为 f(x) 在点  处的海森矩阵，为梯度向量。拟牛顿法的关键在于构建一个与海森矩阵在当前点行为类似的正定对称矩阵，并用其替代 ，从而得到拟牛顿迭代公式：

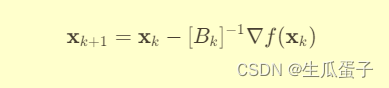
3. 算法原理

拟牛顿法通过维护一个正定对称矩阵来近似海森矩阵，并在每一步迭代中对其进行更新。常用的拟牛顿法如BFGS（Broyden-Fletcher-Goldfarb-Shanno）和L-BFGS（Limited-memory BFGS）采用了以下更新规则：

• BFGS更新：基于当前梯度 和前一步梯度 ，以及搜索方向 和梯度变化，更新 以保持其正定性与对称性。

• L-BFGS更新：为应对大规模优化问题，L-BFGS引入了记忆限制，仅存储最近 m 步的梯度与搜索方向信息，通过这些信息构建一个低秩近似 ​，有效降低了内存需求。

4. 算法实现

当然，接下来我们将通过Python代码实现拟牛顿法中的BFGS算法，并详细讲解其中的关键步骤和逻辑。假设我们要使用BFGS算法求解一个非线性优化问题，即最小化目标函数 。这里以一个具体的函数为例，比如 ​，其中。

Python

import numpy as np

# 定义目标函数 f(x)
def f(x):
    return np.sum(x**2)

# 定义目标函数的一阶导数 f'(x)
def f_prime(x):
    return 2 * x

# 初始化参数
n = 5  # 问题维度
x0 = np.ones(n)  # 初始点
max_iter = 100  # 最大迭代次数
tol = 1e-.jpg  # 收敛精度
B0 = np.eye(n)  # 初始B矩阵（近似海森矩阵）

# BFGS算法实现
def bfgs(f, f_prime, x0, B0, max_iter, tol):
    x = x0
    k = 0
    while k < max_iter:
        # 计算梯度
        gk = f_prime(x)

        # 检查梯度是否接近零，若接近则认为已收敛
        if np.linalg.norm(gk) < tol:
            break

        # 搜索方向 dk = -Bk^(-1) * gk
        dk = -np.linalg.solve(B0, gk)

        # 线搜索确定步长 αk
        alpha_k = line_search(f, x, dk)

        # 更新 x
        x_next = x + alpha_k * dk

        # 计算yk和sk
        sk = x_next - x
        yk = f_prime(x_next) - gk

        # 更新B矩阵
        rho_k = 1 / np.dot(yk, sk)
        B0 += rho_k * np.outer((yk + np.dot(B0, sk)), (yk + np.dot(B0, sk))) - \
              rho_k * np.outer(sk, yk) - rho_k * np.outer(yk, sk)

        # 更新迭代次数和当前点
        x = x_next
        k += 1

    return x

# 简单的Armijo线搜索（可以替换为更复杂的策略）
def line_search(f, x, dk):
    alpha = 1.0
    c = 0.5  # Armijo参数
    beta = 0.5  # 迭代因子

    while True:
        fx = f(x + alpha * dk)
        if fx <= f(x) + c * alpha * np.dot(f_prime(x), dk):
            break
        alpha *= beta

    return alpha

# 应用BFGS算法求解
solution = bfgs(f, f_prime, x0, B0, max_iter, tol)
print("Optimal solution found:", solution)

以上代码实现了BFGS算法的主要逻辑：

1. 初始化：设置初始猜测值 x0、初始B矩阵 B0、最大迭代次数 max_iter、收敛精度 tol。

2. 迭代求解：

   • 计算梯度：使用一阶导数函数 f_prime 计算当前点 x 处的梯度向量 gk。
   • 检查收敛：如果梯度范数小于给定的收敛精度 tol，则认为找到了最优解，跳出循环。
   • 计算搜索方向：计算搜索方向 dk = -Bk^(-1) * gk，即负梯度向量与当前近似海森矩阵的逆的乘积。
   • 线搜索：使用线搜索策略（这里使用了简单的Armijo准则）确定步长 αk。
   • 更新点：根据步长 αk 更新当前点 x 为 x_next = x + αk * dk。
   • 计算yk和sk：计算 sk = x_next - x 和 yk = f_prime(x_next) - gk，用于更新B矩阵。
   • 更新B矩阵：根据BFGS更新规则更新近似海森矩阵 B0。
   • 更新迭代次数：递增迭代次数 k。

3. 返回最优解：当达到最大迭代次数或满足收敛条件时，返回当前点 x 作为最优解。

通过以上代码，我们实现了BFGS算法，并在一个具体的二次函数优化问题上找到了其最小值点。需要注意的是，实际应用中，目标函数和一阶导数函数应根据实际问题进行定义，同时，线搜索策略也可以根据需要选择更复杂的算法以提高搜索效率。

5. 优缺点分析

优点：

• 快速局部收敛：拟牛顿法利用二阶信息，具有类似于牛顿法的二次收敛速率，比单纯依赖一阶信息的梯度下降法更快。
• 不需要海森矩阵求逆：通过构造并更新近似海森矩阵，避免了直接求逆的计算负担和病态问题。
• 适应大规模问题：尤其是L-BFGS，通过记忆限制大大降低了存储需求，适用于大规模优化问题。

缺点：

• 初始矩阵选择敏感：拟牛顿法的收敛速度和稳定性很大程度上取决于初始矩阵的选择，不当的选择可能导致收敛缓慢甚至发散。
• 不适合非凸问题：拟牛顿法在处理非凸或存在多个局部极小值的问题时，可能陷入局部最优而无法找到全局最优。
• 需要计算Hessian-vector积：虽然不需要求逆海森矩阵，但拟牛顿法仍需计算Hessian矩阵与向量的乘积，对于某些复杂模型，这仍然是计算密集型的操作。

6. 案例应用

拟牛顿法在机器学习中有广泛应用，包括但不限于：

• 回归问题：在岭回归、弹性网回归等模型训练中，拟牛顿法用于优化相应的正则化损失函数。
• 分类问题：支持向量机（SVM）的训练过程中，BFGS或L-BFGS常用于优化结构风险最小化问题。
• 神经网络训练：尽管深度学习中通常使用基于梯度的优化器，但在某些特定场景（如小批量、浅层网络），拟牛顿法能够提高训练效率和模型质量。

7. 对比与其他算法

与拟牛顿法相关的其他优化算法包括：

• 牛顿法：直接使用真实的海森矩阵，具有最快的局部收敛速度，但计算和存储成本高，对海森矩阵性质敏感。
• 梯度下降法：仅依赖一阶信息，计算简单，但收敛速度慢，容易陷入局部极小值。
• 随机梯度下降（SGD）及其变种：适用于大规模数据和深度学习模型，通过采样降低计算复杂度，但收敛路径波动较大，需要精细调整学习率。

8. 结论与展望

拟牛顿法作为结合牛顿法与梯度下降法优点的优化算法，在机器学习领域展现出强大的实用性。尽管面临初始矩阵选择敏感、不适合非凸问题等挑战，但通过结合现代优化技术，如动量、自适应学习率等，以及针对大规模数据和深度学习模型的特化设计，拟牛顿法仍有广阔的应用前景。未来研究方向可能包括：

• 改进矩阵更新策略：研发更稳健、适应性更强的矩阵更新规则，以应对各种复杂优化问题。
• 结合现代优化技术：与动量、自适应学习率、二阶梯度估计等技术融合，提升拟牛顿法在非凸优化问题和深度学习模型训练中的表现。
• 分布式与并行计算：利用分布式计算平台和GPU加速，实现大规模拟牛顿法的高效并行计算，适应大数据环境下的机器学习需求。

总之，拟牛顿法作为机器学习优化算法中的重要成员，将继续在理论研究与实际应用中发挥关键作用，推动机器学习技术的持续发展。