无源汇有上下界的最大流

sgu 194 Reactor Cooling

194. Reactor Cooling

time limit per test: 0.5 sec.
memory limit per test: 65536 KB

input: standard
output: standard

The terrorist group leaded by a well known international terrorist Ben Bladen is buliding a nuclear reactor to produce plutonium for the nuclear bomb they are planning to create. Being the wicked computer genius of this group, you are responsible for developing the cooling system for the reactor. 

The cooling system of the reactor consists of the number of pipes that special cooling liquid flows by. Pipes are connected at special points, called nodes, each pipe has the starting node and the end point. The liquid must flow by the pipe from its start point to its end point and not in the opposite direction. 

Let the nodes be numbered from 1 to N. The cooling system must be designed so that the liquid is circulating by the pipes and the amount of the liquid coming to each node (in the unit of time) is equal to the amount of liquid leaving the node. That is, if we designate the amount of liquid going by the pipe from i-th node to j-th as f _ij, (put f _ij = 0 if there is no pipe from node i to node j), for each i the following condition must hold: 


sum(j=1..N, f _ij) = sum(j=1..N, f _ji) 


Each pipe has some finite capacity, therefore for each i and j connected by the pipe must be f _ij ≤ c _ij where c _ij is the capacity of the pipe. To provide sufficient cooling, the amount of the liquid flowing by the pipe going from i-th to j-th nodes must be at least l _ij, thus it must be f _ij ≥ l _ij. 

Given c _ij and l _ij for all pipes, find the amount f _ij, satisfying the conditions specified above. 

Input

The first line of the input file contains the number N (1 ≤ N ≤ 200) - the number of nodes and and M — the number of pipes. The following M lines contain four integer number each - i, j, l _ij and c _ij each. There is at most one pipe connecting any two nodes and 0 ≤ l _ij ≤ c _ij ≤ 10 ⁵ for all pipes. No pipe connects a node to itself. If there is a pipe from i-th node to j-th, there is no pipe from j-th node to i-th. 

Output

On the first line of the output file print YES if there is the way to carry out reactor cooling and NO if there is none. In the first case M integers must follow, k-th number being the amount of liquid flowing by the k-th pipe. Pipes are numbered as they are given in the input file. 

Sample test(s)

Input

Test #1 

4 6 

1 2 1 2 

2 3 1 2 

3 4 1 2 

4 1 1 2 

1 3 1 2 

4 2 1 2 

Test #2 

4 6 

1 2  1 3 

2 3  1 3 

3 4  1 3 

4 1  1 3 

1 3  1 3 

4 2 1 3 

Output

Test #1 

NO 

Test #2 

YES 
1 
2 
3 
2 
1 
1 

题目大意：给出n个节点和m条管子，每根管子都是用来流液体的，连接管子短点的叫节点，水管的流向是单项的，没有管子会只连接着一个节点，也就是说管子连成环状图，构成液体循环制冷系统，保证每个节点的流入量=流出量，每根管子都有其最大流通量Cij，为了保证制冷效果每根管子都有一定的流量下限Lij，即

Lij<=Fij<=Cij,求出每根管子的实际流量Fij，要求满足条件，如果不存在则输出NO；

分析：无源汇点网络流模型：

问题模型：

给定一个加权的有向图，满足：

(1)容量限制条件：

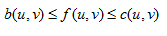
(2)流量平衡条件：

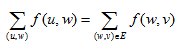
(2)中的即除了源汇外，所有点都满足流量平衡条件，则称G为有源汇网络；否则，即不存在源汇，所有点都满足流量平衡条件，则称G为无源汇网络。

将这类问题由易到难一一解决：

问题[1] 求无源汇的网络有上下界的可行流

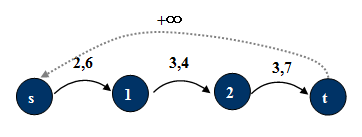
由于下界是一条弧上的流必需要满足的确定值。下面引入必要弧的概念：必要弧是一定流要满的弧。必要弧的构造，将容量下界的限制分离开了，从而构造了一个没有下界的网络G’：

1． 将原弧(u,v)分离出一条必要弧：。（红色表示）

2． 原弧：。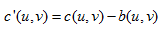

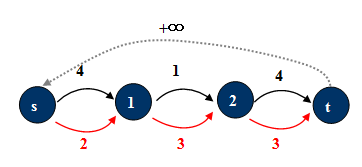
由于必要弧的有一定要满的限制，将必要弧“拉”出来集中考虑：

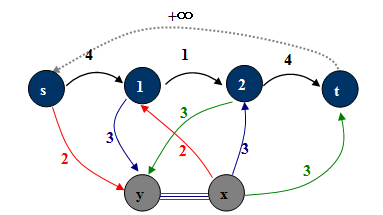
添加附加源x, 附加汇y。想像一条不限上界的(y, x)，用必要弧将它们“串”起来，即对于有向必要弧(u, v)，添加(u, y)，(x, v)，容量为必要弧容量。这样就建立了一个等价的网络。

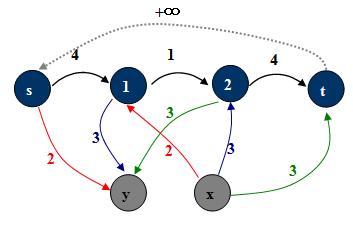
一个无源汇网络的可行流的方案一定是必要弧是满的。若去掉(y, x)后，附加源x到附加汇y的最大流，能使得x的出弧或者y的入弧都满，充要于原图有可行流。

算法：

1. 按上述方法构造新网络(分离必要弧，附加源汇)

2. 求附加源x到附加汇y的最大流

3. 若x的出弧或y的入弧都满，则有解，将必要弧合并回原图；否则，无解。

4.  根据其残留网络，对每条管子的剩余，最大容量Cij-残余ij就是当前管子的实际流量。

程序：

#include"stdio.h"
#include"string.h"
#include"queue"
#define M 222
#define inf 100000000
using namespace std;
struct node
{
    int u,v,w,c,next;
}edge[M*M*3];
int t,head[M],work[M],dis[M];
void init()
{
    t=0;
    memset(head,-1,sizeof(head));
}
void add(int u,int v,int w,int c)
{
    edge[t].u=u;
    edge[t].v=v;
    edge[t].w=w;
    edge[t].c=c;
    edge[t].next=head[u];
    head[u]=t++;

    edge[t].u=v;
    edge[t].v=u;
    edge[t].w=0;
    edge[t].c=c;
    edge[t].next=head[v];
    head[v]=t++;
}
int bfs(int source,int sink)
{
    memset(dis,-1,sizeof(dis));
    queue<int>q;
    q.push(source);
    dis[source]=0;
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=head[u];i!=-1;i=edge[i].next)
        {
            int v=edge[i].v;
            if(edge[i].w&&dis[v]==-1)
            {
                dis[v]=dis[u]+1;
                q.push(v);
                if(v==sink)
                    return 1;
            }
        }
    }
    return 0;
}
int dfs(int cur,int a,int sink)
{
    if(cur==sink)return a;
    for(int &i=work[cur];i!=-1;i=edge[i].next)
    {
        int v=edge[i].v;
        if(edge[i].w&&dis[v]==dis[cur]+1)
        {
            int tt=dfs(v,min(a,edge[i].w),sink);
            if(tt)
            {
                edge[i].w-=tt;
                edge[i^1].w+=tt;
                return tt;
            }
        }
    }
    return 0;
}
int Dinic(int start,int sink)
{
    int ans=0;
    while(bfs(start,sink))
    {
        memcpy(work,head,sizeof(head));
        while(int tt=dfs(start,inf,sink))
            ans+=tt;
    }
    return ans;
}
int main()
{
    int n,m;
    while(scanf("%d%d",&n,&m)!=-1)
    {
        init();
        int source=0;
        int sink=n+1;
        int sum=0;
        while(m--)
        {
            int a,b,c,d;
            scanf("%d%d%d%d",&a,&b,&c,&d);
            add(a,b,d-c,d);//对于每根管子有一个上界容量up和一个下界容量low，我们让这根管子的容量下界变为0，上界为up-low
            add(source,b,c,d);//可是这样做了的话流量就不守恒了，为了再次满足流量守恒，
            add(a,sink,c,d);//即每个节点"入流=出流”，我们增设一个超级源点source和一个超级终点sink
            sum+=c;
        }
        int ans=Dinic(source,sink);
        if(ans<sum)
            printf("NO\n");
        else
        {
            printf("YES\n");
            for(int i=0;i<t;i+=6)
                printf("%d\n",edge[i].c-edge[i].w);
        }
    }
    return 0;
}