无源汇-有上下界-循环流、有源汇-有上下界-可行流

无源汇-有上下界-循环流

循环流

循环流与无源汇，其实是绑定一起的。 有了循环流，他一定是无源汇的，没有beg和ed。
就像有了最大流，他一定是有源汇的，即有唯一的一个beg和ed。
23
最大流： 除了beg和ed外，所有点达到 流量守恒
循环流： 所有点达到 流量守恒，他是一个闭流，所有流量都在内部流动

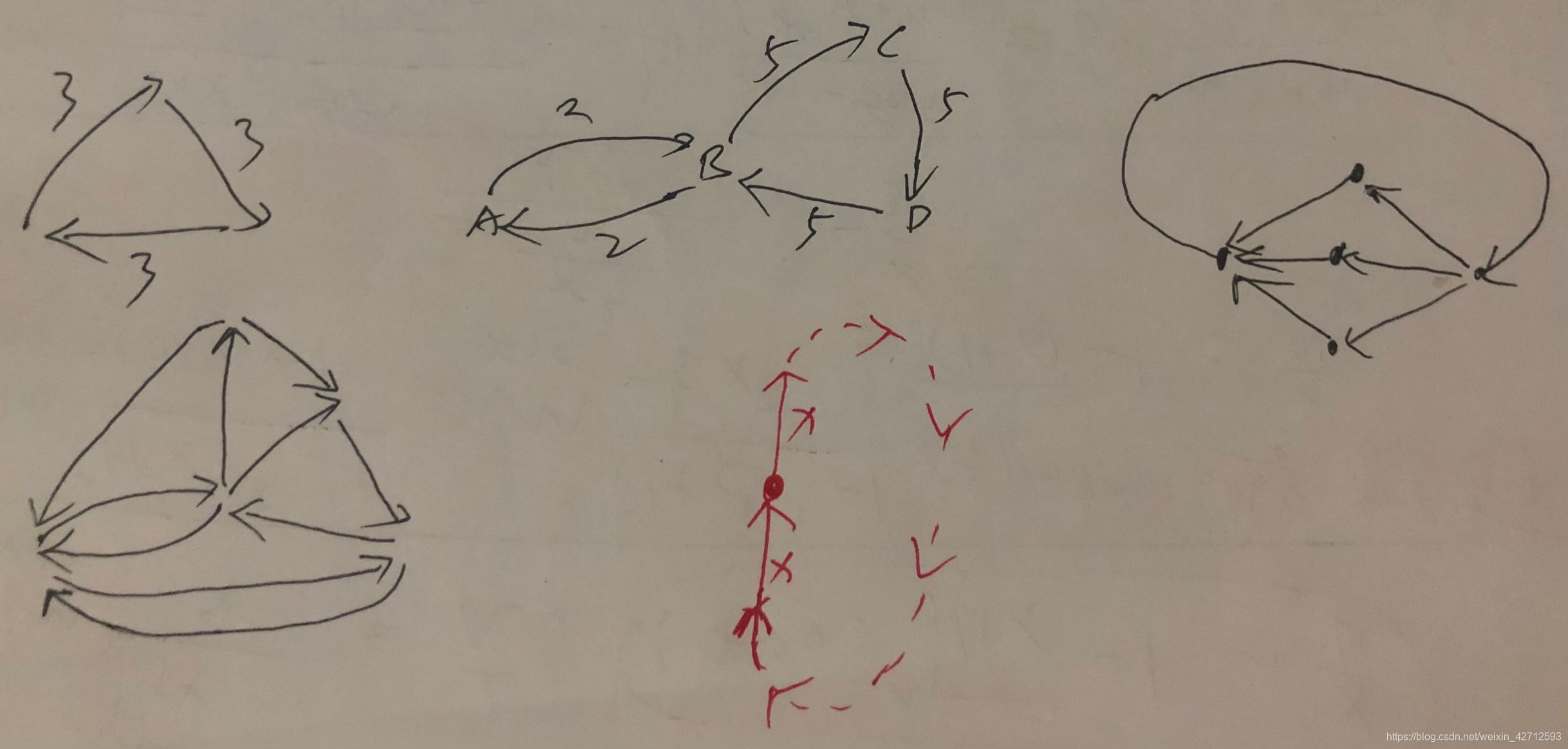
图中展示了4个循环流，可以看到，一个循环流 他的形式，是可以非常非常 复杂的！！！
他不像最大流，可以表示成：beg -> ... -> ed的形式
循环流的结构定义，就是上面说的： 所有点 达到 流量守恒。即，对应到上图中，红色的图形
即看一个循环流，无法整体的看到结构，只能单独去看某一个点的 图
循环流中的每个点，他一定可以抽象为：

• 一条入边 + 一条出边，且边权相同
• 外部用虚线代替，且整体呈现一个环形！！！ （虚线，其实是包含了整个循环流所有边和点的。但不必关系，用虚线表示即可）

---

最大流的流量，即beg流出的 = ed流入的 = 最大流的流量。
而循环流，他的流量一定为0，因为整体是平衡循环的，他没有beg/ed来评判流量的大小。
、、你可能会认为： 比如看上图的那个环，他每个点流量都是相同的，那么就定义该循环流的流量是3。
、、但是，对于不是单环的循环流，就没有办法这样定义了。因为，不是单环的循环流，每个点的流量是不同的。

循环流的流量，可以单独看每个点的流量，无法看整体的。
但每个点的流量是不同的。
比如，图中A点的流量(流入=流出) = 2，而B点的流量是7。这是不同的。

所以，循环流 的流量 的定义，不像最大流一样。
循环流 流量的定义是： 系统总流量 之和（即所有边权的和）

其实，最大流 你把ed->beg多加一条wth=流量的边，他就变成了 循环流。

---

而一个满流来说（即每条边的流量 = 容量），他要么是循环流 要么不是。
具体判断是否是循环流 算法很简单：
令一个点X的delta值为： delta[X] = 所有入边的权重之和 - 所有出边的权重之和
、、如果，所有点的delta值 = 0。等价于： 所有点 达到 流量守恒。等价于： 该流 是循环流。

由于这过于简单， 我们引入： 有上下界的 流网络

有上下界的流网络

普通的流网络，每条边有一个边权wth，表示 该边可以通过[0, wth]的流量。 这也称为： 无下界（下界为0） 的流网络

有上下界的流网络： 每条边有low 和 hig，表示该边必须有流量通过！！ 且通过的流量 是[low, hig]之间的

问： 能否找到一个流，该流是循环流。 找到任意的一个合法循环流即可，不要求是 流量最大/最小的 循环流

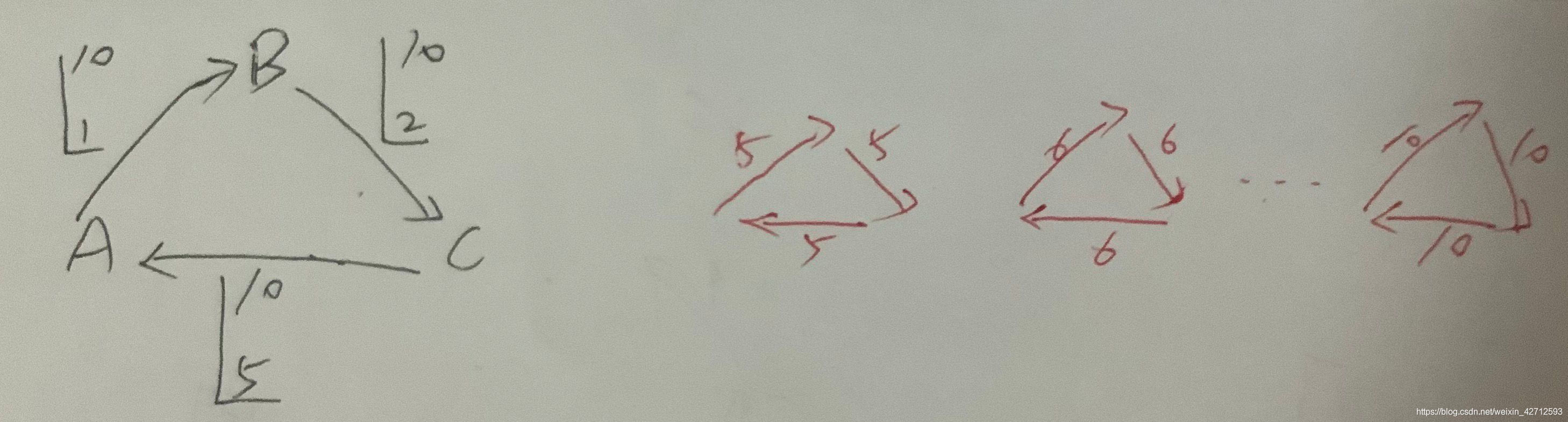
他一共有6种循环流。

---

当然，实际的流网络 是非常非常复杂的，所以，我们必须抽象的去看 去想象，无法来画图分析。

首先，假如存在循环流，那么肯定的是： 该循环流一定包含该图中的所有边，而且每条边的流量 介于[low, hig]之间！！

定义一个流： 包含所有点 和 所有边。边权可以是0

一个base流定义为： 包含所有点 和 所有边，且所有边权 = low值。
比如，上图中，base形如：

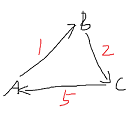
那么，假如存在循环流，该循环流 一定等于： base流 + ans流
（流的相加是： 对应边 的 相加）
这个思路，是求解循环流 的核心

比如，以那个边权为5的循环流来看，他的ans流是：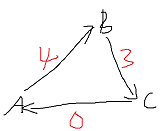

那么，我们问题的关键在于： 能否找到这样的 一个 ans流。

---

当ans流是不存在的，就说明 不存在有循环流。

比如以上图为例。
A->B 的边权为： [1, 10]。 该边在 base流 中，流量为low = 1 该边在 ans流 中， 流量为4
但假如说，A->B 这条边的hig 不再是10，而是4 或比4更小，显然，ans流是不存在的
因为，hig是4，base流已经用了1，还剩下3；而ans流需要4，不够

即，比如一条边 是 [lo, hi]，则：
、、该边 在 base流中， 流量是 lo
、、此时，该边 只剩下了： hi - lo的流量，可以供 ans流来使用。

即，ans流 中的 每条边，一定是 介于 [0, hi - lo]之间的。换句话说， ans流中 每条边 <= [hi - lo]

---

即，此时问题转换为： 有一个流网络，每条边 的边权是： hi - lo， 问是否可以找到一个 ans流
注意，ans流 是一个流，不是循环流。 当然，可能是循环流，前提是base流是循环流

关键是，要找一个怎样的流呢？ 即这个ans流，要满足什么条件呢？

---

此时，回归： 循环流 = base流 + ans流 这个问题上。

循环流，只需要满足一个条件： 所有点 的 delta = 0
一个点的 delta = 所有的出流 - 所有的入流（即，该点 能存储多少流量）

即，满足循环流，条件很简单。 就看所有点的 delta值即可。

即，base流中 某个点的 delta值为： X
则对应的，ans流中 该点的delta值为： -X 即可！！

仔细理解这个原理，这个是求解循环流的 核心！！！

比如还是看样例，A点 在base流中的 delta值为： -4，那么A点 在ans流中 delta值，必须为：4

Delta数组性质

对于任意的一个流，其所有点 的 Delta值 之和，为0 并不需要是 循环流

显然他不是循环流。 其delta之和为： -4 + 1 + 3 = 0

证明要从，delta的定义出发。

• 一个点的delta = 所有入边权之和 - 所有出边权之和
• 每一条边wth，他对终点的delta贡献是wth，对起点的贡献是-1 * wth
  即，所有点的delta之和 里面，有m*2条边，每条边 一加一减。所以，总和为0

---

因为任意一个流 的 Delta之和 为0， 所以，即使一个流 是由 多个相互独立的流 组成，那么，这个流 仍然满足 Delta之和为0.

问题转换

即，现给定一个流网络（每条边的wth为 hig - low）和 一个Delta数组（Delta数组为： 每个在 base流 中的delta值）
求是否可以找到一个ans流，该流满足：每个点x 的delta值为： -1 * Delta[x]

你只需要关心 这个问题，即可！！ 因为顺着上面的推导，就会转换为 这个问题

下图中，Delta的定义是： 出边 - 入边。 这和上面不同... 失误！！ 这倒没有错，因为Delta只表示差值，怎么定义都可以。

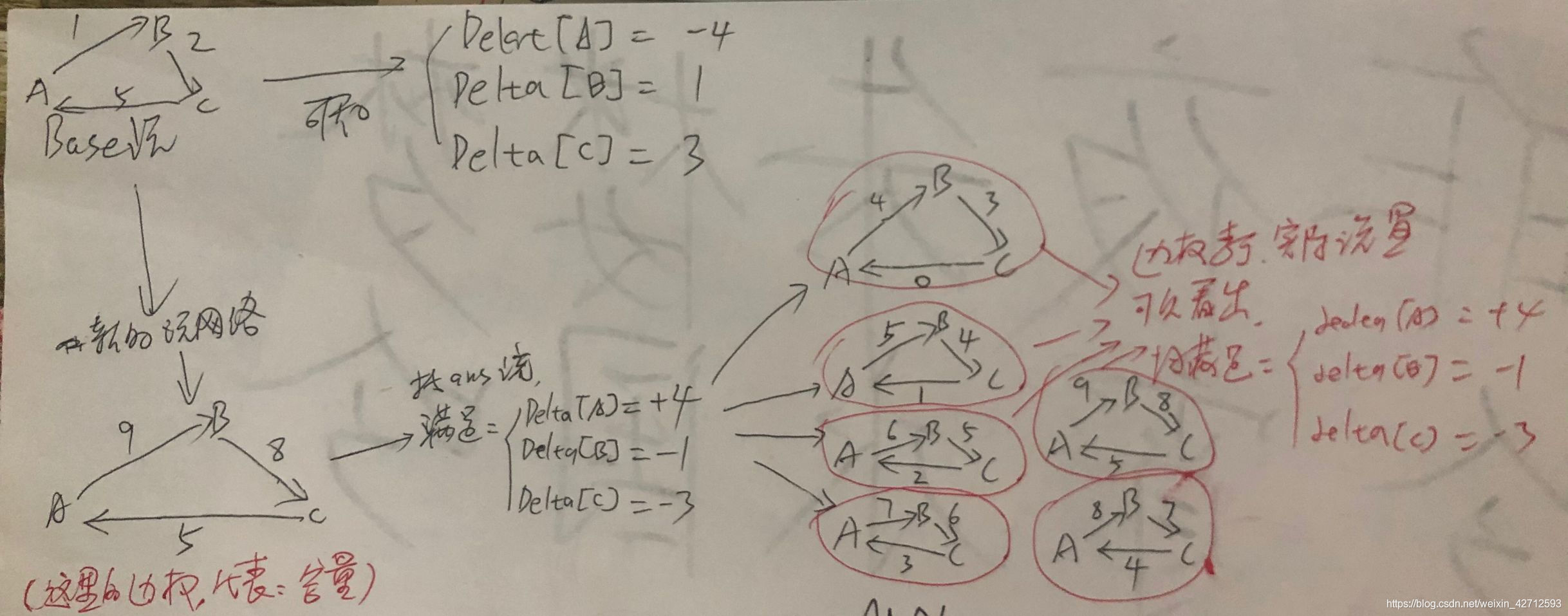
可以看到，ans流的个数（图中画圆圈的）= 之前分析的循环流的个数
而且，所有Delta之和 一定为0。这在之前分析过

当然，现在去求 ans流，依然很困难。
因为，虽然我们知道Delta[A] = +4，但这个Delta是：流量 的差值，不是容量。而我们现在只知道的是：容量。

---

我们分析Delta的含义。
这取决于“你”对Delta的定义！！ 这里我们定义Delta为 净流出。即出- 入
上面一直定义的是：入 - 出.... 但倒没有问题。只是，你必须保证：base流 和 ans流，对delta的定义 是统一的！！
Delta[x] = +4 他表示的是，x这个点，他需要“流出” 4 流量
Delta[x] = -1 表示： x这个点，他需要 “流入” 1 流量

• 所谓“流出” 4流量，流到哪里呢？？？
  其实如果要说，最终要流到哪里，不知道。因为这个ans流，最终是要结合Base流，得到循环流。
  即这个流出4，也就对应到 循环流里的 流出4。而循环流 流出4，也不知道流到哪里。因为是循环的 无终点。
  所以，无需关注“最终”流到哪； 你需要关注 “此时x” 流到哪？
  这个x 要流出4，肯定是，流到 “出边”里面。当然，要保证“出边”容量 >= 4

  ---

  跳跃点：
  有一个虚拟Beg起点，他有一条指向x的边 边权为4，即：beg“流入”给x 有4的流量
  因为最大流，满足：所有非beg/ed的点，流量守恒
  beg给了x有4的流量，到时候在“最大流”里，如果经过x，那么 给了x有4的流量，他也必须要==“流出”==有4的流量。
  这就和上面的“x要流出4的流量”，完全等价了。
  即，x要“净流出”4 <=> beg “流给” x 有4流量

• 上面是“流出”4，即Delta >0的情况。当Delta=-4，即x要流入4
  同样按照上面的思路。x要流入4，肯定是从“入边”获取了4流量
  所谓，x 流入/净获取 4的流量，可以对应为： x “全部流给” ed（x -> ed的边）
  就想象成，ed帮x存储流量，就是x的流量，只是存储到ed里了。

---

所以，原本这个问题是： 给定一个流网络G，和 一个Delta数组。求一个流
该流满足： 每个点x的“净流出(出-入)” = Delta[x] * -1

问题转换为：
建立beg和ed点。
如果该点的delta的含义是： x需要 流出，则beg -> x，边权为|delta|
如果该点的delta的含义是： x需要 流入，则x -> x，边权为|delta|
这里没有绝对说，delta是>0，则beg->x。这是错的！！！ 因为这要看“你”对delta的定义！！！

• 如果你定义delta为“净流入”，则delta < 0时，表示要流出，beg要连接他
• 如果你定义delta为“净流出”，则delta > 0时，表示要流出，beg要连接他

总之，建立完beg和ed点后，然后新加了一些beg->x，x->ed的边后。
对这个图，求最大流。

有个性质：（新加的beg -> ? 的边权之和 等于= 新加的? -> ed 的边权之和，这因为delta的原因）不重要，只是个聊聊

首先，任何一个图，最大流肯定存在。大不了为0呗！！
关键是看这个最大流的 流量。
如果最大流的流量 = beg所有的出边的 边权和。说明，存在ans流
因为，beg的出边beg -> x (wth)，表示 x应该流出wth。只有beg流给x是wth，x才能达到平衡！！

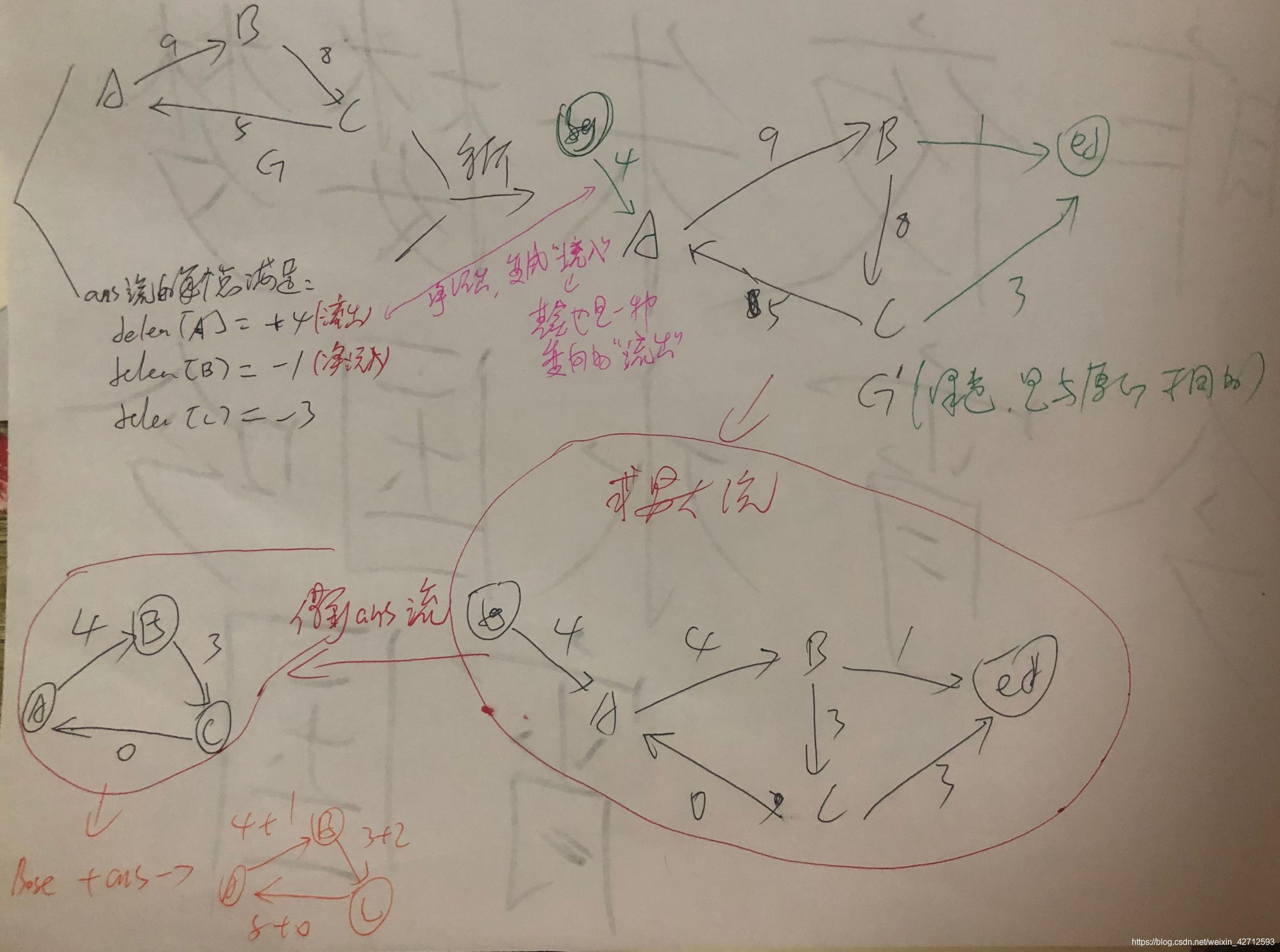
因为，最大流 的流量 是唯一的。所以，只会得到一个ans流
但是，ans流是有很多的 因为循环流有很多。这其实也可以对应到最大流中。

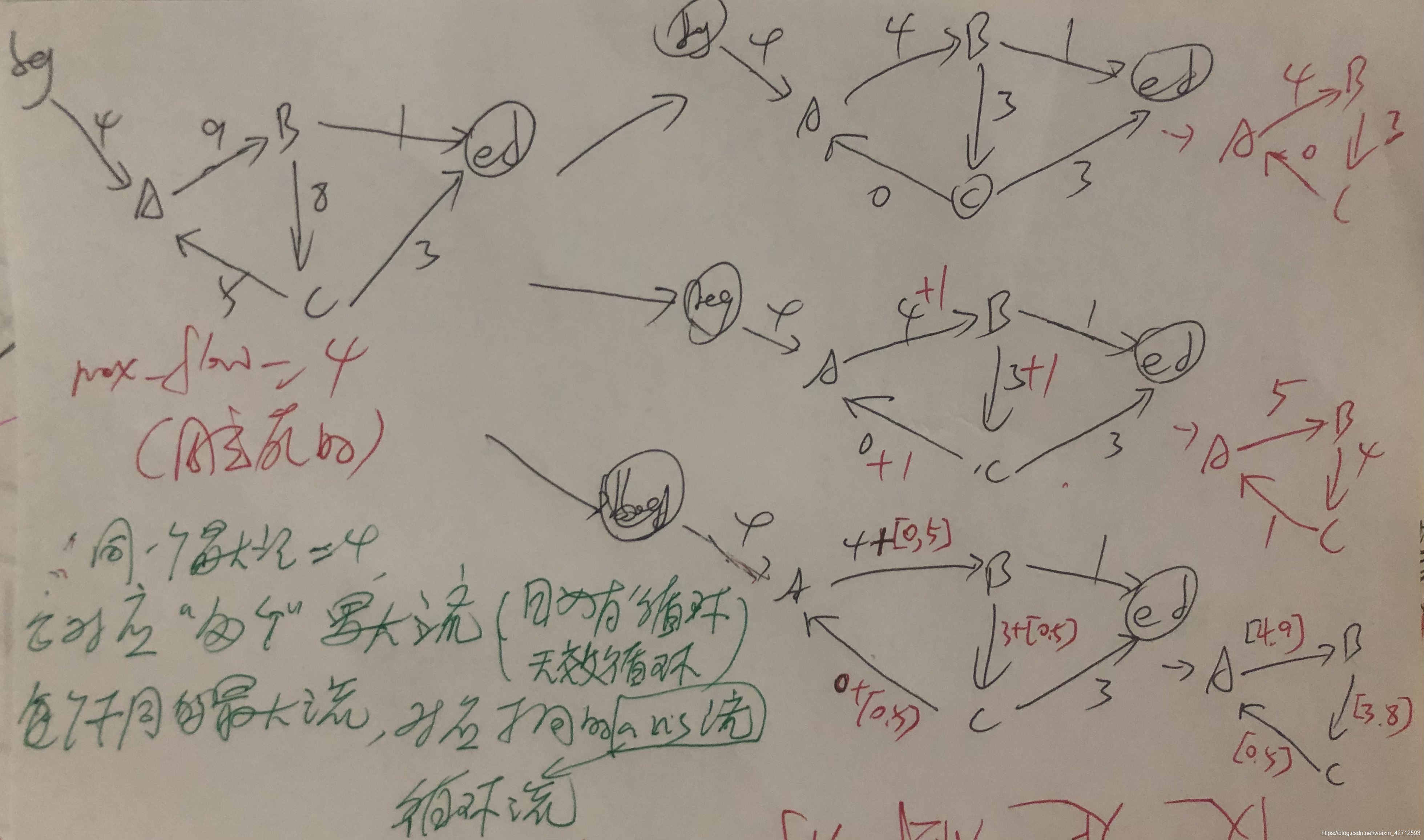
即，最大流的流量是固定的（为4），但他可以对应 很多不同的 最大流，而每个最大流 就对应每个ans流 就对应每个循环流

但我们的最大流算法，肯定不会跑“循环（无效循环）” 因为不会增流。
所以，我们所能获得的最大流（对应 反向边的边权），即是 不走无效循环的最大流，即边权总和最小(4, 3, 0)这个 ans流。
也就对应，== 最终得到的循环流，是流量最小的 循环流！！！==

---

总结

残留网络

原图中：wth[a -> b] = {low, hig}。
存储图（残留网络）中： wth[a -> b] = hig - low, wth[b -> a] = 0

一定要注意，反向边[b -> a] 是0！！！ 不是low！！！

这一点 与 朴素可行流 算法，不同！！！

循环流这里，并不是 可以退回去low的流量！！！ 不可以退回去，因为low是下界，必须满足low下界的界限。
所以，反向边的wth 是0！！！

虚拟起点和终点

循环流算法 求出的最大流的流量 X，如果是“满流”的，则说明 找到了“循环流”）
、、 这个的“满流”是指，令A = 所有正delta之和 = abs(所有负delta之和)。
、、正负的差别，即对应在循环流中 是从虚拟起点Beg流入、还是从虚拟终点Ed流出

这个A（虚拟起点和终点，所有邻接边的边权之和），没有什么其他含义！

这个A，这是为了： 判断 最终求出的最大流 流量X，是否有：X == A，即：A只是为了，判断是否存在 循环流

别无其他意义！！ 因为这个A，他是涉及到 “原图所有点”的delta值， 根据正负值 和 虚拟起点/终点 进行连边

他只是 要配合delta！ 而配合delta的目的，仅仅是为了：判断是否存在 循环流

所以，A只有1个目的： 判断最终 是否A == X，即是否有循环流

流程

• 一个流网络G（可以由多个独立子图组成），每条边 必须通过的流量是： [low, hig]之间
• 得到base流： 每条边是low。根据base流，得到每个点的delta数组
• 建立新的流网络G1： 每条边是hig - low 。 将所有delta *= -1 *=-1的目的是： 让base流 + ans流 = 循环流
• G1建立beg和ed，并且根据新的delta值，建立 有关beg和ed 的边。
• 根据G1流网络，建立残留网络，求最大流。
• 如果，最大流 = 满流。则：base流 + 最大流(残留网络的反向边) = 循环流 满流，为beg的所有临界边权之和

模板

LINK

n个点，m条边。每条边 给定[low, hig]。
求任意一个循环流（输出他的每条边的流量，输出顺序按照录入边的顺序）

SD(&n); SD(