Square Coins
Time Limit: 2000/1000 MS (Java/Others)
Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 7651 Accepted Submission(s): 5180点击打开1398HDU
Problem Description
People in Silverland use square coins. Not only they have square shapes but also their values are square numbers. Coins with values of all square numbers up to 289 (=17^2), i.e., 1-credit coins, 4-credit coins, 9-credit coins, ..., and 289-credit coins, are available in Silverland.
There are four combinations of coins to pay ten credits:
ten 1-credit coins,
one 4-credit coin and six 1-credit coins,
two 4-credit coins and two 1-credit coins, and
one 9-credit coin and one 1-credit coin.
Your mission is to count the number of ways to pay a given amount using coins of Silverland.
There are four combinations of coins to pay ten credits:
ten 1-credit coins,
one 4-credit coin and six 1-credit coins,
two 4-credit coins and two 1-credit coins, and
one 9-credit coin and one 1-credit coin.
Your mission is to count the number of ways to pay a given amount using coins of Silverland.
Input
The input consists of lines each containing an integer meaning an amount to be paid, followed by a line containing a zero. You may assume that all the amounts are positive and less than 300.
Output
For each of the given amount, one line containing a single integer representing the number of combinations of coins should be output. No other characters should appear in the output.
Sample Input
2 10 30 0
Sample Output
1 4 27
Source
Recommend
题目大意:现在有1,4,9,。。。17^2价值的金币,问输入一个n,能够构成n金币的不同选择数有多少,比如n为5,则只有两种,一:五个价值为一,二:一个价值为一,一个价值为四。运用母函数求解。
下面介绍一下母函数:
(百度百科)
生成函数即母函数,是组合数学中尤其是计数方面的一个重要理论和工具。
生成函数
有普通型生成函数和指数型生成函数两种,其中普通型用的比较多。形式上说,普通型
生成函数
用于解决
多重集
的组合问题,而指数型母函数用于解决多重集的排列问题。母函数还可以解决递归数列的通项问题(例如使用母函数解决斐波那契数列的通项公式)。
定义:
对于任意数列a0,a1,a2...an 即用如下方法与一个函数联系起来:
~G(x) = a0 + a1x + a2x^2 + a3x^3 +....+ anx^n
则称G(x)是数列的
生成函数(generating function)
例子:
比较典型的是:A(x) = (1+x)^n~C(n,0),C(n,1),C(n,2),C(n,3),.....,C(n,n)
母函数可分为很多种,包括
普通母函数、
指数母函数、
L级数、
贝尔级数和
狄利克雷级数。对每个序列都可以写出以上每个类型的一个母函数。构造母函数的目的一般是为了解决某个特定的问题,因此选用何种母函数视乎序列本身的特性和问题的类型。
这里先给出两句话,不懂的可以等看完这篇文章再回过头来看:“把组合问题的加法法则和幂级数的t的
乘幂的相加对应起来”
我们首先来看下这个多项式
乘法: (以下图片都可以点击放大)
由此可以看出:
1.x的系数是a1,a2,…an 的单个组合的全体。
2. x2的系数是a1,a2,…a2的两个组合的全体。
………
n. xn的系数是a1,a2,….an的n个组合的全体(只有1个)。
由此得到:如有图
对于序列a0,a1,a2,…构造一函数:
称函数G(x)是序列a0,a1,a2,…的母函数
这里先给出2个例子,等会再结合题目分析:第一种:
有1克、2克、3克、4克的砝码各一 枚,能称出哪几种重量?每种重量各有几种可能方案?
考虑用母函数来解决这个问题:
我们假设x表示砝码,x的指数表示砝码的重量,这样:
1个1克的砝码可以用函数1+x表示,
1个2克的砝码可以用函数1+x∧2表示,
1个3克的砝码可以用函数1+x∧3表示,
1个4克的砝码可以用函数1+x∧4表示,
上面这四个式子懂吗?
我们拿1+x^2来说,前面已经说过,x表示砝码,x的指数表示砝码的重量!即这里就是一个质量为2的砝码,那么前面的
1表示什么?按照上面的理解,1其实应该写为:1*x^0,即1代表重量为2的砝码数量为0个。(理解!)
(维基百科)
普通母函数[编辑]
普通母函数就是最常见的母函数。一般来说,序列 的母函数是:
的母函数是:
如果 是某个离散随机变量的概率质量函数,那么它的母函数被称为一个概率母函数。
是某个离散随机变量的概率质量函数,那么它的母函数被称为一个概率母函数。
多重下标的序列也可以有母函数。例如,序列 的母函数是
的母函数是
-
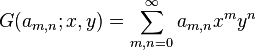 。
。
指数母函数[编辑]
序列 的指数母函数是:
的指数母函数是:
泊松母函数[编辑]
序列 的泊松母函数是:
的泊松母函数是:
L级数[编辑]
序列 的L级数是:
的L级数是:
注意这里的下标 n 从1 而不是0 开始。
贝尔级数[编辑]
关于算术函数 : 和
和  的贝尔级数是:
的贝尔级数是:
狄利克雷级数母函数[编辑]
狄利克雷级数经常被用作母函数,尽管实际上狄利克雷级数并不是严格意义上的形式幂级数。序列 的狄利克雷级数母函数是:
的狄利克雷级数母函数是:
当  是积性函数时狄利克雷级数比较有用,因为这时的母函数可以写成一系列贝尔级数的欧拉积:
是积性函数时狄利克雷级数比较有用,因为这时的母函数可以写成一系列贝尔级数的欧拉积:
如果  是狄利克雷特征,那么它对应的狄利克雷级数母函数被称为狄利克雷L函数。
是狄利克雷特征,那么它对应的狄利克雷级数母函数被称为狄利克雷L函数。
代码实现:
#include <iostream>
using namespace std;
const int _max = 400;
int c1[_max], c2[_max];
int main()
{
int n;
int i, j, k;
while(cin >> n&&n)
{
for(i=0; i<=n; i++)//赋初值
{
c1[i] = 1;//给每个次数的次数赋为1;
c2[i] = 0;//辅助(记忆次数为i的次数的系数)
}
for(i=2; i<=n; i++)//模拟手工计算系数
{
for(j=0; j<=n; ++j)
for(k=0; k+j<=n; k+=i*i)
{
c2[j+k] += c1[j];
}
for(j=0; j<=n; ++j)
{
c1[j] = c2[j];
c2[j] = 0;
}
}
cout << c1[n] << endl;
}
return 0;
}











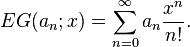
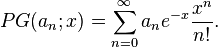
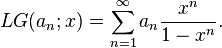
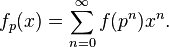
















 150
150

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








