<LeetCode> 题366：斐波那契数列

1. 题目描述：

查找斐波纳契数列中第 N 个数。
所谓的斐波纳契数列是指：前2个数是 0 和 1 。第 i 个数是第 i-1 个数和第i-2 个数的和。斐波纳契数列的前10个数字是：0, 1, 1, 2, 3, 5, 8, 13, 21, 34 …
例如：
给定 1，返回 0
给定 2，返回 1
给定 10，返回 34

2. 思路1：递归求解

long long fib(unsigned int n)  //递归求解
    {
        if(n <= 2)
            return n - 1;
        else
            return fib1(n - 2) + fib1(n - 1);
    }

注意：递归操作，在LeetCode提交时，不通过，显示超时。
原因如下：
递归来解决这一问题，会带来严重的效率问题。比如：要求f(10)，如下图所示:

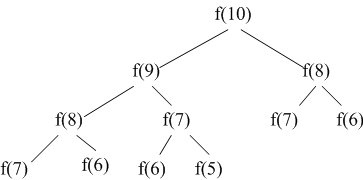
可以看到，上面图示中有很多重复结点，而且重复结点会随着n的增大而急剧增加，意味着计算量也会随着n的增大而急剧增加。事实上该算法的时间复杂度随着n值呈指数增长O((3/2)^n)。

3. 思路2：迭代求解

这种迭代思想就是：先根据f(1)和f(2)计算出f(3)，再根据f(2)和f(3)计算出f(4)……依次类推，最后计算出f(n)。可以看到迭代方法的时间复杂度只有O(n)。

3.1 写法1：

    long long fib(unsigned int n)  //迭代求解
    {
        if(n <= 2)
            return n - 1;

        long long  first = 0;
        long long second = 1;

        for(unsigned int i = 3; i <= n ; i++)
        {
            second = first + second;
            first = second - first;
        }
        return second;
    }   

3.2 写法2：

    long long fib(unsigned int n)  //迭代求解
    {
        if(n <= 2)
            return n - 1;

        long long first = 0;
        long long second = 1;
        long long result;
        for(unsigned int i = 3; i <= n; i++)
        {
            result = first + second;
            first = second;
            second = result;
        }
        return result;
    }

4. 思路3：数组实现

    long long fib(unsigned int n) //数组实现求解
    {
        if(n <= 2)
            return n - 1;
        int *arr = new int[n + 1];
        arr[1] = 0;
        arr[2] = 1;
        for(unsigned int i = 3; i <= n; i++)
        {
            arr[i] = arr[i - 1] + arr[i - 2];
        }
        unsigned int result = arr[n];
        delete arr;
        return result;
    }

5. 思路4：向量实现

    long long fib(unsigned int n) //向量实现求解
    {
        if(n <= 2)
            return n - 1;
        vector<int> vec;
        vec.push_back(0);
        vec.push_back(1);
        vec.reserve(3); //预留空间
        for(unsigned int i = 2; i <= n; i++)
        {
            vec.insert(vec.begin(), vec[0] + vec[1]);
            vec.pop_back(); 
        }
        return vec[0];  
    }

6. 思路5：队列实现

    long long fib(unsigned int n) //队列实现求解
    {
        if(n <= 2)
            return n - 1;
        queue<int> q;
        q.push(0);
        q.push(1);
        for(unsigned int i = 2; i < n; i++)
        {
            q.push(q.front() + q.back());
            q.pop();
        }
        return q.back();    
    }

7. 思路6：通项公式求解

如果我们知道一个数列的通项公式，那么使用公式来计算就容易得多了。对于斐波那契数列来说，由递推公式f(n) = f(n - 1) + f(n - 2)，可以得到f(n)的特征方程为：
x2 = x + 1；从而求出方程的根为：x=(1±√5)/2
所以，存在A，B使得：f(n) = A x ((1+√5)/2)n + B x ((1-√5)/2)n，代入f(0) = 0; f(1) = 1，解得 A=√5/5 ，B=-√5/5 ， 即f(n) = √5/5 x ((1+√5)/2)n - √5/5 x ((1-√5)/2)n
通过公式，我们可以在O(1)的时间内得到f(n)。但公式中引入了无理数，所以不能保证结果的精度。

long long fib(unsigned int n) //通项公式求解
{
    double s = sqrt(5);
    return floor( (pow((1 + s)/2, n) - pow((1 - s)/2, n))/s + 0.5 );
}

注意：这种方法计算出来的结果是以f(0)开始的，也就是说，f(10) = 55(不是34)。