POJ1330 Nearest Common Ancestors(最近公共祖先LCA 并查集+DFS)

Nearest Common Ancestors

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 21069		Accepted: 11050

Description

A rooted tree is a well-known data structure in computer science and engineering. An example is shown below: 

 
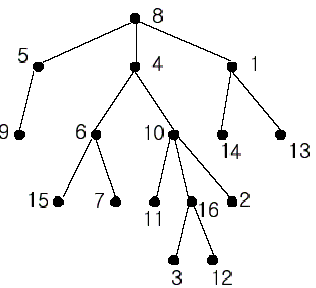
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is. 

For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y. 

Write a program that finds the nearest common ancestor of two distinct nodes in a tree. 

Input

The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N. Each of the next N -1 lines contains a pair of integers that represent an edge --the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.

Output

Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.

Sample Input

2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5

Sample Output

4
3

最近公共祖先(LCA):

1.这个算法基于并查集和深度优先搜索。算法从根开始，对每一棵子树进行深度优先搜索，访问根时，将创建由根结点构建的集合，然后对以他的孩子结点为根的子树进行搜索，使对于 u， v 属于其某一棵子树的 LCA 询问完成。这时将其所有子树结点与根结点合并为一个集合。 对于属于这个集合的结点 u, v 其 LCA 必定是根结点。

2对于最近公共祖先问题，我们先来看这样一个性质，当两个节点（u，v）的最近公共祖先是x时，那么我们可以确定的说，当进行后序遍历的时候，必然先访问完x的所有子树，然后才会返回到x所在的节点。这个性质就是我们使用Tarjan算法解决最近公共祖先问题的核心思想。

      同时我们会想这个怎么能够保证是最近的公共祖先呢？我们这样看，因为我们是逐渐向上回溯的，所以我们每次访问完某个节点x的一棵子树，我们就将该子树所有节点放进该节点x所在的集合，并且我们设置这个集合所有元素的祖先是该节点x。那么到我们完成对一个节点的所有子树的访问时，我们将这个节点标记为已经找到了祖先的点。

       这个时候就体现了Tarjan采用离线的方式解决最近公共祖先的问题特点所在了，所以这个时候就体现了这一点。假设我们刚刚已经完成访问的节点是a，那么我们看与其一同被询问的另外一个点b是否已经被访问过了，若已经被访问过了，那么这个时候最近公共祖先必然是b所在集合对应的祖先c，因为我们对a的访问就是从最近公共祖先c转过来的，并且在从c的子树b转向a的时候，我们已经将b的祖先置为了c，同时这个c也是a的祖先，那么c必然是a、b的最近公共祖先。

       对于一棵子树所有节点，祖先都是该子树的根节点，所以我们在回溯的时候，时常要更新整个子树的祖先，为了方便处理，我们使用并查集维护一个集合的祖先。总的时间复杂度是O(n+q)的，因为dfs是O(n)的，然后对于询问的处理大概就是O(q)的。

AC代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>

using namespace std;

const int maxn = 10001;

int n,fa[maxn];
int rank[maxn];
int indegree[maxn];
int vis[maxn];
vector<int> hash[maxn],Qes[maxn];
int ances[maxn]; //祖先

void init(int n)
{
	for(int i=0;i<=n;i++)
	{
		fa[i] = i;
		rank[i] = 0;
		indegree[i] = 0;
		vis[i] = 0;
		ances[i] = 0;
		hash[i].clear();
		Qes[i].clear();
	}
} 

int find(int x)
{
	if(x != fa[x])
	{
		fa[x] = find(fa[x]);
	}
	return fa[x];
}

void Union(int x,int y)
{
	int fx = find(x);
	int fy = find(y);
	if(fx == fy) return;
	if(rank[fy] < rank[fx])
	{
		fa[fy] = fx;
	}
	else
	{
		fa[fx] = fy;
		if(rank[fx] == rank[fy])
		{
			rank[fy]++; 
		}
	}
}

void Tarjan(int u)
{
	ances[u] = u; //初始化u的祖先为自己 
	int i,size = hash[u].size(); //几个分支
	for(i=0;i<size;i++)
	{
		Tarjan(hash[u][i]); //递归处理儿子
		Union(u,hash[u][i]); //将儿子父亲合并,合并时会将儿子的父亲改为u
		ances[find(u)] = u; //当前结点设置为这个集合的祖先 
	} 
	vis[u] = 1;
	
	//查询
	size = Qes[u].size();
	for(i=0;i<size;i++)
	{
		if(vis[Qes[u][i]] == 1) //即查询的另一个结点开始已经访问过,当前u在此回合访问
		{
			printf("%d\n",ances[find(Qes[u][i])]); //由于递归,此时还是在u
			return;	
		} 
	}
}

int main()
{
	int t;
	int i,j;
	//freopen("1.txt","r",stdin);
	cin>>t;
	while(t--)
	{
		scanf("%d",&n);
		init(n);
		int s,d;
		for(i=1;i<=n-1;i++)
		{
			scanf("%d%d",&s,&d);
			hash[s].push_back(d);
			indegree[d]++; //入度+1 
		}
		scanf("%d%d",&s,&d); //这里可以输入多组询问 
		Qes[s].push_back(d);
		Qes[d].push_back(s);
		for(j=1;j<=n;j++)
		{
			if(indegree[j] == 0) //根结点 
			{
				Tarjan(j);
				break;
			}
		}
	}
	return 0;
}