明氏距离:
明可夫斯基距离(Minkowski Distance)的简称,也被称为闵氏距离。定义的并不是一种距离,而是一组距离。
定义:两个n维变量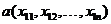
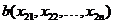
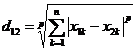
当p=1时,明氏距离即为曼哈顿距离;
当p=2时,明氏距离即为欧氏距离;
当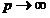
曼哈顿距离:
Manhattan Distance,又叫曼哈坦距离、出租几何距离、城市街区距离(City Block Distance)、棋盘距离。我们可以定义曼哈顿距离的正式意义为L1-距离或城市区块距离,也就是在欧几里得空间的固定直角坐标系上两点所形成的的线段对轴产生的投影距离的总和。
需要注意的是,曼哈顿距离依赖坐标系统的转度,而非系统在坐标轴上的平移或映射。(这句不是很理解,求大神指教)
数学性质:
非负性: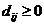
同一性: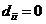
对称性: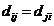
三角不等式: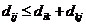
欧式距离:
也称为欧几里得度量(Euclidean Metric),是一个通常采用的距离定义,指在m维空间中两点之间的真实距离或者向量的自然长度(即该点到原点之间的距离)。在二维和三维空间中,欧氏距离就是两点之间的实际距离。
两个n维向量之间的欧氏距离,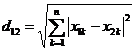

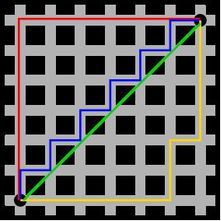
上图中,红色代表曼哈顿距离,绿色代表欧氏距离,也就是直线距离,而蓝色和黄色代表等价的曼哈顿距离。
切比雪夫距离:
Chebyshev Distance,也称为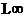
定义,
以数学的观点来看,切比雪夫距离是由一致范数(uniform norm)(或称为上确界范数)所衍生的度量,也是超凸度量(injective metric space)的一种。
国际象棋中,国王走一步能够移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)的最少步数总是max( | x2-x1 | , | y2-y1 | ) 步。
感谢:
感谢网上各位大神的分享^^~~
1.曼哈顿距离:
2.距离汇总:
http://blog.sina.com.cn/s/blog_6f611c300101c5u2.html
3.欧氏距离:
4.切比雪夫距离:







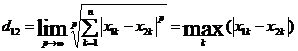
















 1522
1522

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








