很多机器学习的训练算法都是利用梯度下降,朝着梯度的反方向变动,函数值下降最快。
导数
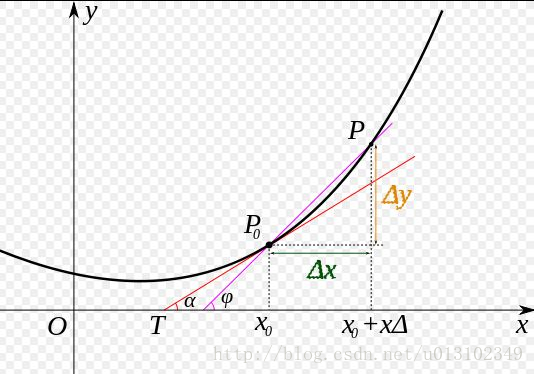
导数可以表示函数曲线上的切线斜率。 除了切线的斜率,导数还表示函数在该点的变化率。
导数代表了在自变量变化趋于无穷小的时候,函数值的变化与自变量变化的比值代表了导数,几何意义有该点的切线。物理意义有该时刻的(瞬时)变化率。
在一元函数中,只有一个自变量变动,也就是说只存在一个方向的变化率,这也就是为什么一元函数没有偏导数的原因。
偏导数
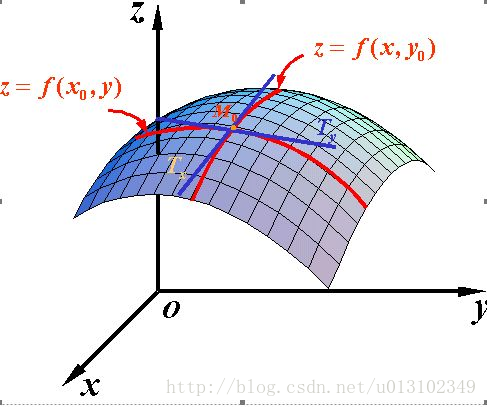
偏导数至少涉及到两个自变量,以两个自变量为例,z=f(x,y) . 从导数到偏导数,也就是从曲线来到了曲面. 曲线上的一点,其切线只有一条。但是曲面的一点,切线有无数条。偏导数是指的是多元函数沿坐标轴的变化率。
指的是函数在y方向不变,函数值沿着x轴方向的变化率
 指的是函数在x方向不变,函数值沿着y轴方向的变化率
指的是函数在x方向不变,函数值沿着y轴方向的变化率
- 偏导数
 就是曲面被平面
就是曲面被平面 所截得的曲面在点
所截得的曲面在点 处的切线
处的切线对x轴的斜率
- 偏导数
 就是曲面被平面
就是曲面被平面 所截得的曲面在点
所截得的曲面在点 处的切线
处的切线对y轴的斜率
偏导数指的是多元函数沿坐标轴的变化率,但是我们往往很多时候要考虑多元函数沿任意方向的变化率,那么就引出了方向导数.
方向导数
设 为一个二元函数,
为一个二元函数, 为一个单位向量,如果下列的极限值存在
为一个单位向量,如果下列的极限值存在
 此方向导数记为
此方向导数记为
则称这个极限值是 沿着
沿着 方向的方向导数,那么随着
方向的方向导数,那么随着 的不同,我们可以求出任意方向的方向导数.
的不同,我们可以求出任意方向的方向导数.
简化计算如下:
设 ,
,
那么我们可以得到:
 (
( 为向量
为向量 与向量
与向量 之间的夹角)
之间的夹角)
 要取得最大值,也就是当
要取得最大值,也就是当 为0度的时候,也就是向量
为0度的时候,也就是向量 (这个方向是一直在变,在寻找一个函数变化最快的方向)与向量
(这个方向是一直在变,在寻找一个函数变化最快的方向)与向量 (这个方向当点固定下来的时候,它就是固定的)平行的时候,方向导数最大.方向导数最大,也就是单位步伐,函数值朝这个反向变化最快.
(这个方向当点固定下来的时候,它就是固定的)平行的时候,方向导数最大.方向导数最大,也就是单位步伐,函数值朝这个反向变化最快.
函数值下降最快的方向就是和 向量相同的方向.那么此时我把A向量命名为梯度(当一个点确定后,梯度方向是确定的),也就是说明了为什么梯度方向是函数变化率最大的方向了!!!
向量相同的方向.那么此时我把A向量命名为梯度(当一个点确定后,梯度方向是确定的),也就是说明了为什么梯度方向是函数变化率最大的方向了!!!
参考:
[1] https://zhuanlan.zhihu.com/p/24913912








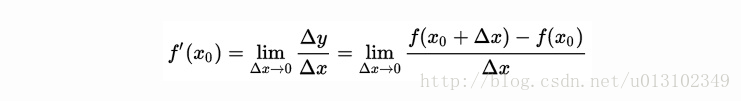















 1145
1145

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








