优化方法之最速下降法（采用解析法求解步长+直接采用一阶导求解下降方向+python 代码实现（可直接拿走使用））

最速下降法是我们在求解优化问题时经常使用的方法，它的核心思想在于步长以及方向向量的选择和求解。最速下降法要求我们在每一步都尽可能下降最大的函数值。它的核心算法步骤可见下：

其中，在确定方向向量后，我们需要求解该方向上的最优步长，以使步长下降最多。步长的求解主要有以下两种方法：

这里，我们选择解析法求解最佳步长。它的核心思想在方法二中已有体现。步长选取过大或者过小都是不利于函数下降的。以下是几幅比较直观的图。

我们这里对以下函数使用最速下降法求解其最优值。

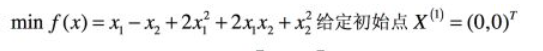
这里就依据前述算法编写代码如下：

# 这个程序实现最速下降法的实现和测试，所谓最速下降法，是指我们是指应该在某一点沿着当前点下降最大的函数点前进，这里注意需要寻找最优
#步长和下降方向，我们可以直接求得方向导数。以导数的负数即可（这里有什么规范化和不规范化，其实问题本质都一样)在确定方向后，需要求解
#最优步长，以使函数下降最快。步长过大或者过小都不能达到我们的要求。

from sympy import*
import math
from matplotlib import pyplot as plt
import numpy as np

def Obj(x1,x2):
    value=x1-x2+2*math.pow(x1,2)+2*x1*x2+math.pow(x2,2)
    return value
def Jac_x1(x1,x2):
    value=1+4*x1+2*x2
    return value
def Jac_x2(x1,x2):
    value=-1+2*x1+2*x2
    return value

def Error(x1,x2):
    value=math.sqrt(math.pow(x1,2)+math.pow(x2,2))
    return value

#指定初始值
Epsilon=0.5#设定误差的初始值
X=[0,0]
Direction=[-Jac_x1(X[0],X[1]),-Jac_x2(X[0],X[1])]#指定负梯度方向作为下降方向
t=sympy.symbols('t') # t是我们的步长
Temp_x=[X[0]+t*Direction[0],X[1]+t*Direction[1]]
z=diff(Temp_x[0]-Temp_x[1]+2*Temp_x[0]*Temp_x[0]+2*Temp_x[0]*Temp_x[1]+Temp_x[1]*Temp_x[1])
Lambda=sympy.solve(z) #求解最优步长，该步长使我们的函数下降最快
Current_error=Error(Jac_x1(X[0],X[1]),Jac_x2(X[0],X[1]))

#算法迭代部分
Value=[]
Minimum=Obj(X[0],X[1])
error=[]
lamb=[]
while Current_error>Epsilon:
    #保存数据
    error.append(Current_error)
    Value.append(Obj(X[0],X[1]))
    lamb.append(Lambda)
    if Minimum>Obj(X[0],X[1]):
        Minimum=Obj(X[0],X[1])
        if(Minimum==-1.25):
            break
    #print(Minimum)
    #更新相关数据 
    temp1=X[0]+Lambda[0]*Direction[0]
    temp2=X[1]+Lambda[0]*Direction[1]
    X[0]=temp1
    X[1]=temp2
    #X=[X[0]+Lambda*Direction[0],X[1]+Lambda*Direction[1]]#算法核心迭代部分，更新点
    Direction=[-Jac_x1(X[0],X[1]),-Jac_x2(X[0],X[1])] #更新方向向量
    Temp_x=[X[0]+t*Direction[0],X[1]+t*Direction[1]]
    z=diff(Temp_x[0]-Temp_x[1]+2*Temp_x[0]*Temp_x[0]+2*Temp_x[0]*Temp_x[1]+Temp_x[1]*Temp_x[1])
    Lambda=sympy.solve(z) #更新Lambda
print("最小值是：{}".format(Obj(X[0],X[1])))
print("迭代次数是：{}".format(len(Value)))
print("最小值点是：",X)
plt.plot(Value)
plt.title("The changes of function value")
plt.xlabel("The number of iteration")
plt.ylabel("The value of function")
fig=plt.figure()
plt.plot(error)
plt.title("The changes of error")
plt.xlabel("The number of iteration")
plt.ylabel("The value of error")

fig1=plt.figure()
plt.plot(lamb)
plt.xlabel("The number of iteration")
plt.ylabel("The value of Lambda")
plt.title("The changes of Lambda in the process of iteration")

代码运行结果见下图所示：

可见，程序运行仅迭代23次就给出了最优值-1.25，可见最速下降算法的运行速度还是比较快的。
下面几幅图分别展示了函数值、方向向量绝对值、以及步长随着迭代次数增加的变化情况。同学们可以根据实际情况查看加深理解，大家也可以将代码进行改编以求解其余情况的函数并加深理解。



祝好！