不知道大家在使用JS的过程中有没有发现某些浮点数运算的时候,得到的结果存在
精度问题:比如0.1 + 0.2 = 0.30000000000000004以及7 * 0.8 = 5.6000000000000005等等。
究竟是什么原因造成了这个问题?实际上是因为计算机内部的信息都是由 二进制方式表示的,即0和1组成的各种编码,但由于 某些浮点数没办法用二进制准确的表示出来,也就带来了一系列精度问题。当然这也 不是JS独有的问题。
接下来让我们 以0.1+0.2为例,深入理解一下 浮点数的运算方法,以及使用JS时应该如何 规避这个问题。这个问题很基础,但也很有了解的必要,大家就当是复习一下 《计算机组成原理》吧。
② 小数部分:乘2取整数部分,若小数不为0则继续乘2,直至小数部分为0将取出的整数位正序排列。(若小数部分无法为零,根据有效位数要求取得相应数值,位数后一位0舍1入进行取舍)
利用上述方法,我们尝试一下将0.1转成二进制:
0.1 * 2 = 0.2 - - - - - - - - - - 取0
0.2 * 2 = 0.4 - - - - - - - - - - 取0
0.4 * 2 = 0.8 - - - - - - - - - - 取0
0.8 * 2 = 1.6 - - - - - - - - - - 取1
0.6 * 2 = 1.2 - - - - - - - - - - 取1
0.2 * 2 = 0.4 - - - - - - - - - - 取0
......
算到这就会发现小数部分再怎么继续乘都 不会等于0,所以 二进制是没办法精确表示0.1的。
那么0.1的二进制表示是:0.000110011......0011...... (0011无限循环)
而0.2的二进制表示则是:0.00110011......0011...... (0011无限循环)
而具体应该保存多少位数,则 需要根据使用的是什么标准来确定,也就是下一节所要讲到的内容。
根据IEEE 754标准,任意一个二进制浮点数都可以表示成以下形式:
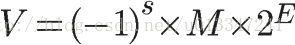
S为数符,它表示浮点数的正负(0正1负);M为有效位(尾数);E为阶码,用移码表示,阶码的真值都被加上一个常数(偏移量)。
① 单精度:

这是32位的浮点数,最高的1位是符号位S,后面的8位是指数E,剩下的23位为尾数(有效数字)M;
其 真值为:
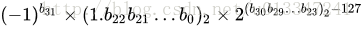
② 双精度:
究竟是什么原因造成了这个问题?实际上是因为计算机内部的信息都是由 二进制方式表示的,即0和1组成的各种编码,但由于 某些浮点数没办法用二进制准确的表示出来,也就带来了一系列精度问题。当然这也 不是JS独有的问题。
接下来让我们 以0.1+0.2为例,深入理解一下 浮点数的运算方法,以及使用JS时应该如何 规避这个问题。这个问题很基础,但也很有了解的必要,大家就当是复习一下 《计算机组成原理》吧。
通过后面的几个小章节,将会大致为大家介绍以下几个方面内容:
● 浮点数的二进制表示方式
● IEEE 754 标准是什么
● 避开浮点数计算精度问题的方案
● 测试框架(Mocha)的基本用法
一、计算机的运算方式
㈠ 如何将小数转成二进制
② 小数部分:乘2取整数部分,若小数不为0则继续乘2,直至小数部分为0将取出的整数位正序排列。(若小数部分无法为零,根据有效位数要求取得相应数值,位数后一位0舍1入进行取舍)
利用上述方法,我们尝试一下将0.1转成二进制:
0.1 * 2 = 0.2 - - - - - - - - - - 取0
0.2 * 2 = 0.4 - - - - - - - - - - 取0
0.4 * 2 = 0.8 - - - - - - - - - - 取0
0.8 * 2 = 1.6 - - - - - - - - - - 取1
0.6 * 2 = 1.2 - - - - - - - - - - 取1
0.2 * 2 = 0.4 - - - - - - - - - - 取0
......
算到这就会发现小数部分再怎么继续乘都 不会等于0,所以 二进制是没办法精确表示0.1的。
那么0.1的二进制表示是:0.000110011......0011...... (0011无限循环)
而0.2的二进制表示则是:0.00110011......0011...... (0011无限循环)
而具体应该保存多少位数,则 需要根据使用的是什么标准来确定,也就是下一节所要讲到的内容。
㈡ IEEE 754 标准
根据IEEE 754标准,任意一个二进制浮点数都可以表示成以下形式:
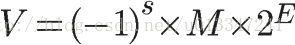
S为数符,它表示浮点数的正负(0正1负);M为有效位(尾数);E为阶码,用移码表示,阶码的真值都被加上一个常数(偏移量)。
尾数部分M通常都是规格化表示的,即非"0"的尾数其第一位总是"1",而这一位也称隐藏位,因为存储时候这一位是会被省略的。比如保存1.0011时,只保存0011,等读取的时候才把第一位的1加上去,这样做相当于多保存了1位有效数字。
① 单精度:

这是32位的浮点数,最高的1位是符号位S,后面的8位是指数E,剩下的23位为尾数(有效数字)M;
其 真值为:
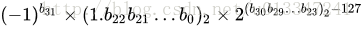
② 双精度:








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 676
676

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








