Nearest Common Ancestors
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 17144 | Accepted: 9128 |
Description
A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:
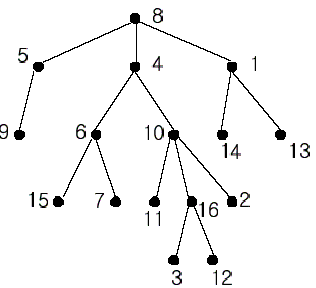
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.

In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.
Input
The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N. Each of the next N -1 lines contains a pair of integers that represent an edge --the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.
Output
Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.
Sample Input
2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5
Sample Output
4
3
Source
Taejon 2002
传送门:【POJ】1330 Nearest Common Ancestors
题目大意:这丫就是在解释LCA(最近公共祖先)。。。给你n个节点的树,接下来n-1条边,每条边描述为(u,v),表示u是v的父节点,最后给你两个点,让你求这两个点的最近公共祖先。
题目分析:刚学了倍增的在线LCA,顺便敲一下。
不懂倍增的可以看下这篇: 【UVa】11354 Bond 最小生成树,动态LCA,倍增思想
代码如下:
传送门:【POJ】1330 Nearest Common Ancestors
题目大意:这丫就是在解释LCA(最近公共祖先)。。。给你n个节点的树,接下来n-1条边,每条边描述为(u,v),表示u是v的父节点,最后给你两个点,让你求这两个点的最近公共祖先。
题目分析:刚学了倍增的在线LCA,顺便敲一下。
不懂倍增的可以看下这篇: 【UVa】11354 Bond 最小生成树,动态LCA,倍增思想
代码如下:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std ;
#define REPF( i , a , b ) for ( int i = a ; i <= b ; ++ i )
#define REPV( i , a , b ) for ( int i = a ; i >= b ; -- i )
#define LOGF( i , n ) for ( int i = 1 ; ( 1 << i ) < n ; ++ i )
#define EDGE( i , x ) for ( int i = adj[x] ; ~i ; i = edge[i].n )
#define clear( a , x ) memset ( a , x , sizeof a )
const int MAXN = 10005 ;
const int MAXE = 20005 ;
const int LOGN = 20 ;
struct Edge {
int v , n ;
Edge ( int var = 0 , int next = 0 ) :
v ( var ) , n ( next ) {}
} ;
struct LCA {
Edge edge[MAXE] ;
int adj[MAXN] , cntE ;
int anc[MAXN][LOGN] ;
int fa[MAXN] ;
int deep[MAXN] ;
int n ;
void init () {
cntE = 0 ;
clear ( adj , -1 ) ;
}
void addedge ( int u , int v ) {
edge[cntE] = Edge ( v , adj[u] ) ;
adj[u] = cntE ++ ;
edge[cntE] = Edge ( u , adj[v] ) ;
adj[v] = cntE ++ ;
}
void dfs ( int u , int p ) {
EDGE ( i , u ) {
int v = edge[i].v ;
if ( v != p ) {
fa[v] = u ;
deep[v] = deep[u] + 1 ;
dfs ( v , u ) ;
}
}
}
void preProcess () {
REPF ( i , 1 , n ) {
anc[i][0] = fa[i] ;
LOGF ( j , n )
anc[i][j] = -1 ;
}
LOGF ( j , n )
REPF ( i , 1 , n )
if ( ~anc[i][j - 1] )
anc[i][j] = anc[anc[i][j - 1]][j - 1] ;
}
int query ( int p , int q ) {
int log = 0 ;
if ( deep[p] < deep[q] )
swap ( p , q ) ;
LOGF ( i , deep[p] + 1 )
++ log ;
REPV ( i , log , 0 )
if ( deep[p] - ( 1 << i ) >= deep[q] )
p = anc[p][i] ;
if ( p == q )
return p ;
REPV ( i , log , 0 )
if ( ~anc[p][i] && anc[p][i] != anc[q][i] )
p = anc[p][i] , q = anc[q][i] ;
return fa[p] ;
}
} ;
LCA L ;
bool in[MAXN] ;
void work () {
int u , v , root ;
clear ( in , false ) ;
scanf ( "%d" , &L.n ) ;
L.init () ;
REPF ( i , 1 , L.n - 1 ) {
scanf ( "%d%d" , &u , &v ) ;
L.addedge ( u , v ) ;
in[v] = true ;
}
REPF ( i , 1 , L.n )
if ( !in[root = i] )
break ;
L.deep[root] = 0 ;
L.dfs ( root , 0 ) ;
L.preProcess () ;
scanf ( "%d%d" , &u , &v ) ;
printf ( "%d\n" , L.query ( u , v ) ) ;
}
int main () {
int T ;
scanf ( "%d" , &T ) ;
while ( T -- )
work () ;
return 0 ;
}























 1102
1102

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








