群体优化算法---鳄鱼优化算法介绍，使用乳腺癌威斯康星诊断数据集进行神经网络训练

介绍

鳄鱼优化算法（Crocodile Optimization Algorithm, COA）是一种基于鳄鱼行为和生态系统的元启发式优化算法。COA 模拟了鳄鱼的捕猎策略、繁殖和社会行为来解决优化问题

鳄鱼优化算法的基本原理

鳄鱼优化算法的灵感来自于鳄鱼的生活方式，包括捕猎策略和群体行为。该算法通过模拟鳄鱼在水域和陆地的活动来寻找最优解

主要步骤

初始化：

初始化种群，包括鳄鱼的位置、速度等参数。
设置算法参数，如种群大小、最大迭代次数等。
捕猎策略：

鳄鱼在水中捕猎时，通常会在一段时间内保持静止，等待猎物接近，然后迅速出击。该行为可以通过探索和开发平衡来建模。
使用当前种群位置和速度更新每只鳄鱼的位置。
繁殖和社会行为：

鳄鱼的繁殖行为可以模拟种群的更新。优良的个体会产生更多的后代，而劣质个体会被淘汰。
社会行为包括个体之间的信息共享，促进全局最优解的搜索。
适应度评估：

计算每只鳄鱼在新位置的适应度值，根据适应度值来更新最优解。
更新最优解：

如果当前迭代中找到的解比之前的最优解更好，则更新最优解。
迭代：

重复捕猎策略、繁殖和社会行为、适应度评估和更新最优解的步骤，直到达到最大迭代次数或满足终止条件

适用领域

鳄鱼优化算法作为一种元启发式优化算法，适用于各种优化问题，包括：

函数优化：求解数学函数的最小值或最大值。
组合优化：如旅行商问题、背包问题等。
工程优化：如结构优化、参数优化等。
机器学习：如神经网络训练、特征选择等。

结论

鳄鱼优化算法通过模拟鳄鱼的捕猎策略、繁殖和社会行为来解决复杂的优化问题。它结合了探索和开发的平衡，具有较强的全局搜索能力和收敛速度。通过不断地调整和改进，COA在许多应用中展示了其优越性

本文示例

我们将采用鳄鱼优化算法来用乳腺癌威斯康星诊断数据数据集进行神经网络训练

核心代码

function COA_NN
    % 参数设置
    pop_size = 50; % 种群大小
    max_iter = 100; % 最大迭代次数
    lower_bound = -1; % 权重下界
    upper_bound = 1; % 权重上界
    
    % 加载数据集
    data = load('breast_cancer_data.mat');
    X = data.X;
    y = data.y;
    
    % 初始化神经网络架构
    input_size = size(X, 2);
    hidden_layer1_size = 64;
    hidden_layer2_size = 32;
    hidden_layer3_size = 16;
    output_size = 1;
    
    % 计算神经网络权重的总数
    dim = (input_size + 1) * hidden_layer1_size + ...
          (hidden_layer1_size + 1) * hidden_layer2_size + ...
          (hidden_layer2_size + 1) * hidden_layer3_size + ...
          (hidden_layer3_size + 1) * output_size;
    
    % 初始化种群
    population = lower_bound + (upper_bound - lower_bound) .* rand(pop_size, dim);
    fitness = zeros(pop_size, 1);
    
    % 计算初始种群的适应度
    for i = 1:pop_size
        fitness(i) = fitness_function(population(i, :), X, y, input_size, hidden_layer1_size, hidden_layer2_size, hidden_layer3_size, output_size);
    end
    
    [best_fitness, best_idx] = min(fitness);
    best_solution = population(best_idx, :);
    fitness_history = zeros(max_iter, 1);
    fitness_history(1) = best_fitness;
    
    % 主要优化过程
    for t = 2:max_iter
        for i = 1:pop_size
            % 更新鳄鱼位置
            new_position = population(i, :) + rand(1, dim) .* (best_solution - population(i, :));
            new_position = min(max(new_position, lower_bound), upper_bound);
            new_fitness = fitness_function(new_position, X, y, input_size, hidden_layer1_size, hidden_layer2_size, hidden_layer3_size, output_size);
            
            % 更新种群和适应度
            if new_fitness < fitness(i)
                population(i, :) = new_position;
                fitness(i) = new_fitness;
            end
        end
        
        % 选择优良个体进行繁殖
        [sorted_fitness, sorted_idx] = sort(fitness);
        population = population(sorted_idx, :);
        fitness = fitness(sorted_idx);
        
        for i = round(pop_size / 2):pop_size
            parents = population(randperm(round(pop_size / 2), 2), :);
            population(i, :) = mean(parents) + randn(1, dim) * 0.1;
            population(i, :) = min(max(population(i, :), lower_bound), upper_bound);
            fitness(i) = fitness_function(population(i, :), X, y, input_size, hidden_layer1_size, hidden_layer2_size, hidden_layer3_size, output_size);
        end
        
        % 更新最优解
        [current_best_fitness, best_idx] = min(fitness);
        if current_best_fitness < best_fitness
            best_fitness = current_best_fitness;
            best_solution = population(best_idx, :);
        end
        
        % 记录当前迭代的最佳适应度
        fitness_history(t) = best_fitness;
        fprintf('Iteration %d, Best Fitness: %.4f\n', t, best_fitness);
    end
    
    % 使用最优权重训练最终模型并评估
    final_model = create_model(best_solution, input_size, hidden_layer1_size, hidden_layer2_size, hidden_layer3_size, output_size);
    predictions = final_model(X);
    accuracy = sum((predictions > 0.5) == y) / length(y);
    fprintf('Final Model Accuracy: %.4f\n', accuracy);
    
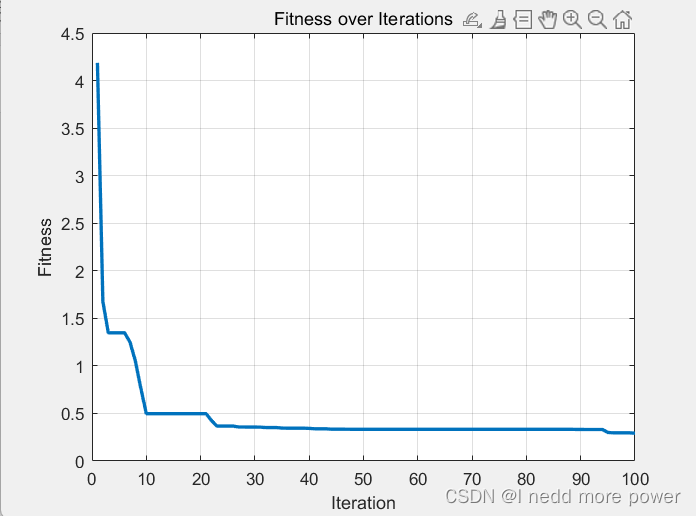
    % 可视化适应度变化
    figure;
    plot(fitness_history, 'LineWidth', 2);
    xlabel('Iteration');
    ylabel('Fitness');
    title('Fitness over Iterations');
    grid on;
    
    % 可视化最终模型的预测结果
    figure;
    scatter(1:length(y), y, 'b', 'filled');
    hold on;
    scatter(1:length(predictions), predictions, 'r', 'filled');
    xlabel('Sample Index');
    ylabel('Prediction / True Value');
    title('Model Predictions vs True Values');
    legend('True Values', 'Predictions');
    grid on;
end

function fitness = fitness_function(weights, X, y, input_size, hidden_layer1_size, hidden_layer2_size, hidden_layer3_size, output_size)
    model = create_model(weights, input_size, hidden_layer1_size, hidden_layer2_size, hidden_layer3_size, output_size);
    predictions = model(X);
    % 为防止对数计算出现NaN，添加一个小的epsilon
    epsilon = 1e-8;
    predictions = min(max(predictions, epsilon), 1 - epsilon);
    loss = -mean(y .* log(predictions) + (1 - y) .* log(1 - predictions)); % 交叉熵损失
    fitness = loss;
end

function model = create_model(weights, input_size, hidden_layer1_size, hidden_layer2_size, hidden_layer3_size, output_size)
    % 将扁平化权重向量转换为权重矩阵
    W1 = reshape(weights(1:(input_size + 1) * hidden_layer1_size), input_size + 1, hidden_layer1_size);
    W2 = reshape(weights((input_size + 1) * hidden_layer1_size + 1: ...
                        (input_size + 1) * hidden_layer1_size + (hidden_layer1_size + 1) * hidden_layer2_size), hidden_layer1_size + 1, hidden_layer2_size);
    W3 = reshape(weights((input_size + 1) * hidden_layer1_size + (hidden_layer1_size + 1) * hidden_layer2_size + 1: ...
                        (input_size + 1) * hidden_layer1_size + (hidden_layer1_size + 1) * hidden_layer2_size + (hidden_layer2_size + 1) * hidden_layer3_size), hidden_layer2_size + 1, hidden_layer3_size);
    W4 = reshape(weights((input_size + 1) * hidden_layer1_size + (hidden_layer1_size + 1) * hidden_layer2_size + (hidden_layer2_size + 1) * hidden_layer3_size + 1:end), hidden_layer3_size + 1, output_size);
    
    model = @(X) forward_pass(X, W1, W2, W3, W4);
end

function output = forward_pass(X, W1, W2, W3, W4)
    % 添加偏置项
    X = [X, ones(size(X, 1), 1)];
    
    
    hidden_layer2_output = [hidden_layer2_output, ones(size(hidden_layer2_output, 1), 1)];
    hidden_layer3_input = hidden_layer2_output * W3;
    hidden_layer3_output = relu(hidden_layer3_input);
    
    hidden_layer3_output = [hidden_layer3_output, ones(size(hidden_layer3_output, 1), 1)];
    output_layer_input = hidden_layer3_output * W4;
    output = sigmoid(output_layer_input);
end

function y = sigmoid(x)
    y = 1 ./ (1 + exp(-x));
end

function y = relu(x)
    y = max(0, x);
end

效果

完整代码获取

微信扫一扫，回复"鳄鱼优化算法"即可获取完整代码