(1)基本概念
图像的点运算包含线性变换和非线性变换,其中,非线性变换分为对数变换、幂次变换、指数变换等。这几种变换都能有效的改变图像的亮度和对比度,然而,其中的参数却需要人为设定,设定的好,才能得到效果。那么问题来了,是否存在一种变换,不需要人为设定参数,就可以改善图像的对比度?
显然,从图像对比度的定义出发(简单来说,对比度就是最黑与最白亮度单位的相除值),如果一幅图像占据的灰度级范围更大,且每一像素的灰度级分布均匀,则该图像就具有更高的对比度,更丰富的细节,以及更大的信息量。那么,现在的任务,就是找到一个变换函数s=T(r),使得灰度级r经过映射后得到的灰度级s,呈均匀分布。
上一篇博文中强调过,像素的灰度级r可以看作是一个随机变量(没错,就是随机变量,曾经以为这辈子除了考试再不会用到的概率论知识,竟然这么快就见面了),则灰度级的分布就可以用随机变量的累计分布函数和累计概率密度函数来刻画和描述。捋一捋现在的条件,不难发现,像素原灰度级r已知,r的概率密度函数P(r)已知,变换后灰度级s的概率分布P(s)也已知(因为期望得到的灰度级s呈均匀分布,假设像素最高灰度级为L,则P(s)=1/(L-1))。很简单,这就相当于概率论中的一个题型“求一维随机变量函数的分布问题,即已知X的概率分布,求Y=g(X)的概率分布”。遇到这种问题,我就记着老师讲的“什么都不要管,先把F(y)=P{Y<y}=P{g(X)<y}写上去,两分到手了”,可是,很快我发现推不下去了。翻翻书,《数字图像处理_原理与实践》的作者在这里是直接“由概率理论可以得到如下公式…”,我不是作者,没有他那样扎实的数学功底,如果我也一带而过,那不叫懂,而是不懂装懂。
于是查阅各种资料,终于发现,我漏了一个很重要的条件:为了使变换后的灰度级从白到黑的次序不变,变换函数T(r)应该满足单调递增的条件(仔细想想确是这样)。从下面的图上看更明显,s和r是一一对应的关系,即S<s就等价于R<r,有了这一步,就能继续推导:
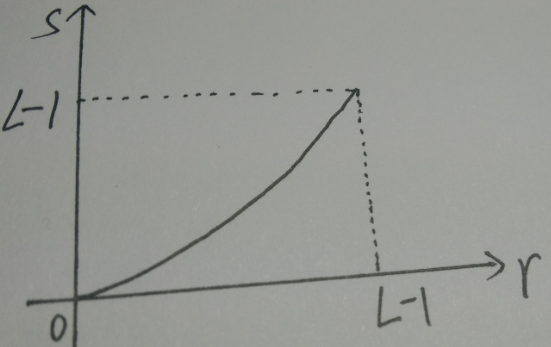

然而,上述推导方法是以灰度级r为连续随记变量为基础讨论的,当灰度级r为离散值时,显然可用如下公式表示:
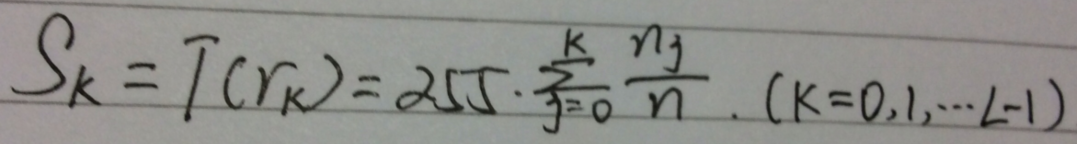
至此为止,推导结束(第一次感觉数学这么有用,哈哈)。
(2)编码实现
MATLAB中图像处理工具箱提供了用以实现灰度均衡算法的函数histeq(),语法形式为:
[J,T]=histeq(I,n);
J=histeq(I,n) ;
其中,I表示原始图像,J是灰度均衡化后的输出图像,T是变换矩阵(即返回能将图像I的直方图变换成图像J的直方图的变换T)。参数n指定直方图均衡化后的灰度级数,默认值为64。
下面是自己根据上面数学推导的结果,分步骤完成的灰度均衡化算法代码的实现。
% ***************************Copyright 2016[c]**************************
% ************************Declaration************************************
% File name: histogram_equalization
% Author: 靖harry
% Date: 16-Jul-2016 11:07:03
% Version Number: 1.0
% Abstract:
% Enhance the contrast of images by transforming the values in an
% intensity image, so that the histogram of the output image
% approximately equalized histogram.
% *********************************end*********************************
clear
clc
I1=imread('8.jpg');
I1=rgb2gray(I1);
[m,n]=size(I1);
L=256; % total gray_level
%count the number of gray_level pixels respectively.%
nk=zeros(1,256);
for i1=1:m
for j1=1:n
nk(I1(i1,j1)+1)=nk(I1(i1,j1)+1) + 1 ;
end
end
pk=nk/(m*n); % calculate the PDF of original gray_level.
%figure out the values of transformed gray_level.%
sk=zeros(1,256);
for i2=1:L
for j2=1:i2
sk(i2)=sk(i2)+pk(j2);
end
end
sk=fix((L-1)*sk); % take integer part of variabel sk.
%确定映射关系,得到新图像I2.%
I2=I1;
for i3=1:m
for j3=1:n
I2(i3,j3)=sk(I1(i3,j3)+1);
end
end
I3=histeq(I1,256);%用matlab自带函数实现均匀化得到的图像
subplot(3,2,1),imshow(I1),title('original image');
subplot(3,2,2),imhist(I1),title('original histogram');
subplot(3,2,3),imshow(I2),title('transformed image by myself');
subplot(3,2,4),imhist(I2),title('transformed histogram by myself');
subplot(3,2,5),imshow(I3),title('transformed image by matlab');
subplot(3,2,6),imhist(I3),title('transformed histogram by matlab');
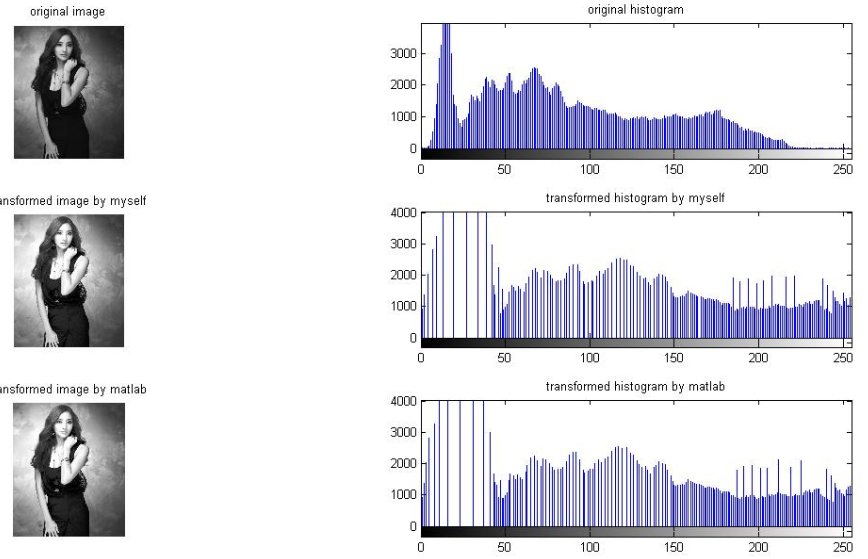
以下是分别用几张图像实验的效果:
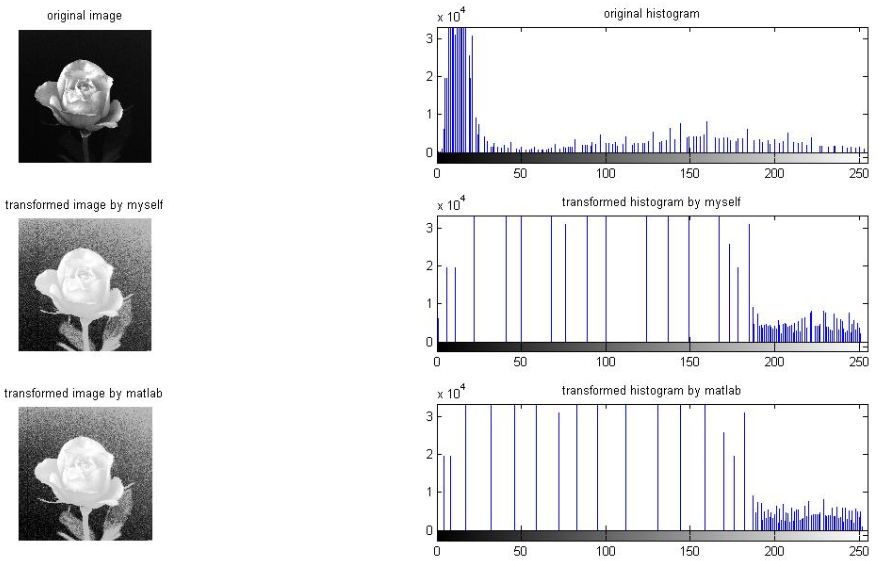
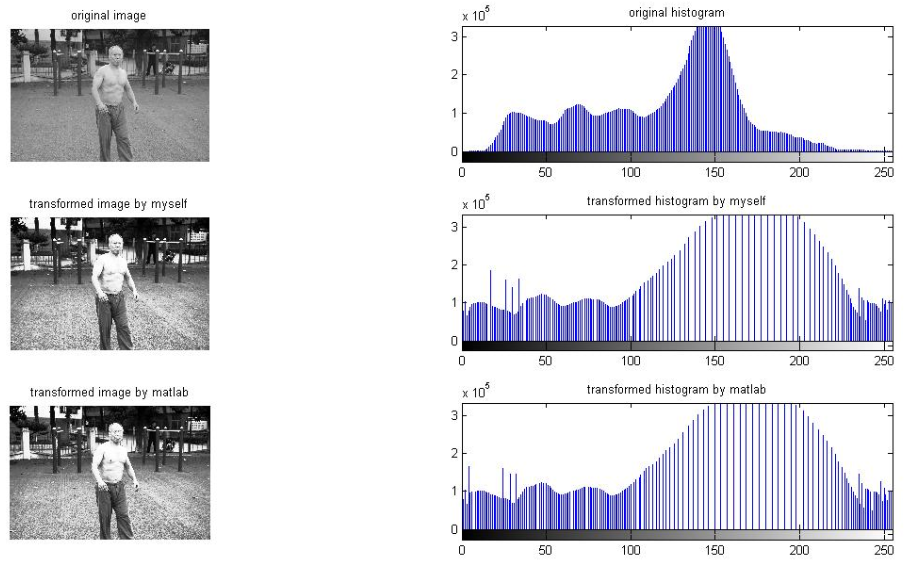
再来一张
 :
:
 :
:






















 4366
4366

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








