《毁灭战士》中使用 BSP 的巧妙之处_on visible surface generation by a priori tree str-CSDN博客

本文链接：https://blog.csdn.net/u013669912/article/details/142504495

注：本文为 “BSP” 相关文章合辑。

英文引文机翻，未校。

如有异常，请看原文。

How Much of a Genius-Level Move Was Using Binary Space Partitioning in Doom?

06 Nov 2019

In 1993, id Software released the first-person shooter Doom, which quickly became a phenomenon. The game is now considered one of the most influential games of all time.

1993 年，id Software 发布了第一人称射击游戏《毁灭战士》（Doom），它迅速成为一种现象。这款游戏如今被认为是有史以来最具影响力的游戏之一。

A decade after Doom’s release, in 2003, journalist David Kushner published a book about id Software called Masters of Doom, which has since become the canonical account of Doom’s creation. I read Masters of Doom a few years ago and don’t remember much of it now, but there was one story in the book about lead programmer John Carmack that has stuck with me. This is a loose gloss of the story (see below for the full details), but essentially, early in the development of Doom, Carmack realized that the 3D renderer he had written for the game slowed to a crawl when trying to render certain levels. This was unacceptable, because Doom was supposed to be action-packed and frenetic. So Carmack, realizing the problem with his renderer was fundamental enough that he would need to find a better rendering algorithm, started reading research papers. He eventually implemented a technique called “binary space partitioning,” never before used in a video game, that dramatically sped up the Doom engine.

在《毁灭战士》发布十年后的 2003 年，记者大卫・库什纳（David Kushner）出版了一本关于 id Software 的书，名为《毁灭战士大师》（Masters of Doom），这本书此后成为了关于《毁灭战士》创作的权威记述。我几年前读过《毁灭战士大师》，现在已经记不太清了，但书中有一个关于首席程序员约翰・卡马克（John Carmack）的故事让我印象深刻。以下是这个故事的大致内容（详细内容见下文），但基本上，在《毁灭战士》开发的早期，卡马克意识到他为游戏编写的 3D 渲染器在渲染某些关卡时速度变得极其缓慢。这是不可接受的，因为《毁灭战士》本应是充满动作和刺激的。于是，卡马克意识到他的渲染器的问题非常根本，他需要找到一种更好的渲染算法，于是开始阅读研究论文。他最终实现了一种名为 “二叉空间分割”（binary space partitioning）的技术，此前从未在视频游戏中使用过，这极大地提高了《毁灭战士》引擎的速度。

That story about Carmack applying cutting-edge academic research to video games has always impressed me. It is my explanation for why Carmack has become such a legendary figure. He deserves to be known as the archetypal genius video game programmer for all sorts of reasons, but this episode with the academic papers and the binary space partitioning is the justification I think of first.

卡马克将前沿学术研究应用于视频游戏的这个故事一直令我印象深刻。这就是我认为卡马克成为传奇人物的原因。他有各种各样的理由被视为典型的天才视频游戏程序员，但他阅读学术论文并应用二叉空间分割技术的这个事件是我首先想到的理由。

Obviously, the story is impressive because “binary space partitioning” sounds like it would be a difficult thing to just read about and implement yourself. I’ve long assumed that what Carmack did was a clever intellectual leap, but because I’ve never understood what binary space partitioning is or how novel a technique it was when Carmack decided to use it, I’ve never known for sure. On a spectrum from Homer Simpson to Albert Einstein, how much of a genius-level move was it really for Carmack to add binary space partitioning to Doom?

显然，这个故事令人印象深刻，因为 “二叉空间分割” 听起来像是一种很难仅仅通过阅读就能自行实现的技术。我一直认为卡马克的做法是一次聪明的智力飞跃，但由于我一直不明白二叉空间分割是什么，也不知道卡马克决定使用它时这项技术有多新颖，所以我一直不能确定。在从荷马・辛普森到阿尔伯特・爱因斯坦的范围内，卡马克在《毁灭战士》中加入二叉空间分割技术到底是多么天才的举动呢？

I’ve also wondered where binary space partitioning first came from and how the idea found its way to Carmack. So this post is about John Carmack and Doom, but it is also about the history of a data structure: the binary space partitioning tree (or BSP tree). It turns out that the BSP tree, rather interestingly, and like so many things in computer science, has its origins in research conducted for the military.

我还想知道二叉空间分割最初来自哪里，以及这个想法是如何传到卡马克那里的。所以这篇文章是关于约翰・卡马克和《毁灭战士》的，但它也是关于一种数据结构的历史：二叉空间分割树（或 BSP 树）。事实证明，BSP 树非常有趣，就像计算机科学中的许多事物一样，它起源于为军事进行的研究。

That’s right: E1M1, the first level of Doom, was brought to you by the US Air Force.

没错：《毁灭战士》的第一关 E1M1 是由美国空军带来的。

The VSD Problem 可视表面判定（VSD）问题

The BSP tree is a solution to one of the thorniest problems in computer graphics. In order to render a three-dimensional scene, a renderer has to figure out, given a particular viewpoint, what can be seen and what cannot be seen. This is not especially challenging if you have lots of time, but a respectable real-time game engine needs to figure out what can be seen and what cannot be seen at least 30 times a second.

BSP 树是解决计算机图形学中最棘手问题之一的方法。为了渲染一个三维场景，渲染器必须根据特定的视角确定哪些是可见的，哪些是不可见的。如果你有足够的时间，这并不是特别具有挑战性，但一个像样的实时游戏引擎需要每秒至少 30 次确定哪些是可见的，哪些是不可见的。

This problem is sometimes called the problem of visible surface determination. Michael Abrash, a programmer who worked with Carmack on Quake (id Software’s follow-up to Doom), wrote about the VSD problem in his famous Graphics Programming Black Book:
I want to talk about what is, in my opinion, the toughest 3-D problem of all: visible surface determination (drawing the proper surface at each pixel), and its close relative, culling (discarding non-visible polygons as quickly as possible, a way of accelerating visible surface determination). In the interests of brevity, I’ll use the abbreviation VSD to mean both visible surface determination and culling from now on.

这个问题有时被称为可视表面判定问题。曾与卡马克在《雷神之锤》（Quake，id Software 继《毁灭战士》之后的作品）中合作的程序员迈克尔・阿布拉什（Michael Abrash）在他著名的《图形编程黑皮书》中写道：
我想谈谈在我看来最棘手的 3D 问题：可视表面判定（在每个像素上绘制正确的表面）及其近亲，剔除（尽快丢弃不可见多边形，这是加速可视表面判定的一种方法）。为了简洁起见，从现在起，我将使用缩写 VSD 来表示可视表面判定和剔除。

Why do I think VSD is the toughest 3-D challenge? Although rasterization issues such as texture mapping are fascinating and important, they are tasks of relatively finite scope, and are being moved into hardware as 3-D accelerators appear; also, they only scale with increases in screen resolution, which are relatively modest.

为什么我认为 VSD 是最棘手的 3D 挑战呢？虽然诸如纹理映射等光栅化问题很有趣且重要，但它们的范围相对有限，并且随着 3D 加速器的出现正在被转移到硬件中；而且，它们只随着屏幕分辨率的适度提高而扩展。

In contrast, VSD is an open-ended problem, and there are dozens of approaches currently in use. Even more significantly, the performance of VSD, done in an unsophisticated fashion, scales directly with scene complexity, which tends to increase as a square or cube function, so this very rapidly becomes the limiting factor in rendering realistic worlds.

相比之下，VSD 是一个开放性问题，目前有几十种方法在使用。更重要的是，以简单方式进行的 VSD 性能直接与场景复杂度相关，场景复杂度往往呈平方或立方函数增长，因此这很快就成为渲染逼真世界的限制因素。

Abrash was writing about the difficulty of the VSD problem in the late ’90s, years after Doom had proved that regular people wanted to be able to play graphically intensive games on their home computers. In the early ’90s, when id Software first began publishing games, the games had to be programmed to run efficiently on computers not designed to run them, computers meant for word processing, spreadsheet applications, and little else. To make this work, especially for the few 3D games that id Software published before Doom, id Software had to be creative. In these games, the design of all the levels was constrained in such a way that the VSD problem was easier to solve.

阿布拉什在 90 年代后期写下了关于 VSD 问题的难度，此时距离《毁灭战士》证明普通人希望能够在他们的家用电脑上玩图形密集型游戏已经过去了好几年。在 90 年代初期，当 id Software 首次发布游戏时，这些游戏必须被编程为在并非为运行它们而设计的计算机上高效运行，这些计算机是用于文字处理、电子表格应用程序等的。为了实现这一点，特别是对于 id Software 在《毁灭战士》之前发布的少数 3D 游戏，id Software 必须要有创意。在这些游戏中，所有关卡的设计都受到限制，以便更容易解决 VSD 问题。

For example, in Wolfenstein 3D, the game id Software released just prior to Doom, every level is made from walls that are axis-aligned. In other words, in the Wolfenstein universe, you can have north-south walls or west-east walls, but nothing else. Walls can also only be placed at fixed intervals on a grid—all hallways are either one grid square wide, or two grid squares wide, etc., but never 2.5 grid squares wide. Though this meant that the id Software team could only design levels that all looked somewhat the same, it made Carmack’s job of writing a renderer for Wolfenstein much simpler.

例如，在《德军总部 3D》（Wolfenstein 3D）中，这是 id Software 在《毁灭战士》之前发布的游戏，每个关卡都是由轴向对齐的墙壁构成的。换句话说，在《德军总部》的世界里，你只能有南北向或东西向的墙壁，没有其他方向的。墙壁也只能以固定的间隔放置在网格上 —— 所有的走廊要么是一个网格方块宽，要么是两个网格方块宽等等，但绝不是 2.5 个网格方块宽。虽然这意味着 id Software 团队只能设计出看起来都有些相似的关卡，但这使得卡马克为《德军总部》编写渲染器的工作简单了很多。

The Wolfenstein renderer solved the VSD problem by “marching” rays into the virtual world from the screen. Usually a renderer that uses rays is a “raycasting” renderer—these renderers are often slow, because solving the VSD problem in a raycaster involves finding the first intersection between a ray and something in your world, which in the general case requires lots of number crunching. But in Wolfenstein, because all the walls are aligned with the grid, the only location a ray can possibly intersect a wall is at the grid lines. So all the renderer needs to do is check each of those intersection points. If the renderer starts by checking the intersection point nearest to the player’s viewpoint, then checks the next nearest, and so on, and stops when it encounters the first wall, the VSD problem has been solved in an almost trivial way. A ray is just marched forward from each pixel until it hits something, which works because the marching is so cheap in terms of CPU cycles. And actually, since all walls are the same height, it is only necessary to march a single ray for every column of pixels.

《德军总部》的渲染器通过从屏幕向虚拟世界 “投射” 光线来解决 VSD 问题。通常使用光线的渲染器是 “光线投射” 渲染器 —— 这些渲染器通常很慢，因为在光线投射器中解决 VSD 问题需要找到光线与世界中物体的第一个交点，在一般情况下这需要大量的数值计算。但在《德军总部》中，因为所有的墙壁都与网格对齐，光线可能与墙壁相交的唯一位置就是网格线。所以渲染器只需要检查这些交点。如果渲染器从检查离玩家视角最近的交点开始，然后检查次近的，依此类推，当遇到第一面墙时停止，那么 VSD 问题就以一种几乎微不足道的方式解决了。光线从每个像素向前投射，直到碰到东西，这之所以可行是因为这种投射在 CPU 周期方面成本很低。实际上，由于所有的墙壁高度相同，对于每一列像素只需要投射一条光线。

This rendering shortcut made Wolfenstein fast enough to run on underpowered home PCs in the era before dedicated graphics cards. But this approach would not work for Doom, since the id team had decided that their new game would feature novel things like diagonal walls, stairs, and ceilings of different heights. Ray marching was no longer viable, so Carmack wrote a different kind of renderer. Whereas the Wolfenstein renderer, with its ray for every column of pixels, is an “image-first” renderer, the Doom renderer is an “object-first” renderer. This means that rather than iterating through the pixels on screen and figuring out what color they should be, the Doom renderer iterates through the objects in a scene and projects each onto the screen in turn.

这种渲染捷径使得《德军总部》在没有专用显卡的时代能够在性能较弱的家用电脑上快速运行。但这种方法对《毁灭战士》不起作用，因为 id 团队决定他们的新游戏将包含诸如对角墙壁、楼梯和不同高度的天花板等新颖元素。光线投射不再可行，所以卡马克编写了一种不同类型的渲染器。《德军总部》的渲染器为每一列像素都投射光线，是一种 “图像优先” 的渲染器，而《毁灭战士》的渲染器是一种 “物体优先” 的渲染器。这意味着《毁灭战士》的渲染器不是遍历屏幕上的像素并确定它们应该是什么颜色，而是遍历场景中的物体，并依次将每个物体投影到屏幕上。

In an object-first renderer, one easy way to solve the VSD problem is to use a z-buffer. Each time you project an object onto the screen, for each pixel you want to draw to, you do a check. If the part of the object you want to draw is closer to the player than what was already drawn to the pixel, then you can overwrite what is there. Otherwise you have to leave the pixel as is. This approach is simple, but a z-buffer requires a lot of memory, and the renderer may still expend a lot of CPU cycles projecting level geometry that is never going to be seen by the player.

在物体优先的渲染器中，解决 VSD 问题的一种简单方法是使用 z 缓冲区。每次你将一个物体投影到屏幕上时，对于你想要绘制的每个像素，你都要进行一次检查。如果你想要绘制的物体部分比已经绘制在该像素上的物体更靠近玩家，那么你可以覆盖那里的内容。否则，你必须保持像素不变。这种方法很简单，但 z 缓冲区需要大量内存，而且渲染器可能仍然会花费大量 CPU 周期来投影玩家永远看不到的关卡几何图形。

In the early 1990s, there was an additional drawback to the z-buffer approach: On IBM-compatible PCs, which used a video adapter system called VGA, writing to the output frame buffer was an expensive operation. So time spent drawing pixels that would only get overwritten later tanked the performance of your renderer.

在 20 世纪 90 年代初期，z 缓冲区方法还有一个额外的缺点：在使用名为 VGA 的视频适配器系统的 IBM 兼容 PC 上，写入输出帧缓冲区是一个昂贵的操作。因此，花费在绘制那些稍后会被覆盖的像素上的时间会严重影响渲染器的性能。

Since writing to the frame buffer was so expensive, the ideal renderer was one that started by drawing the objects closest to the player, then the objects just beyond those objects, and so on, until every pixel on screen had been written to. At that point the renderer would know to stop, saving all the time it might have spent considering far-away objects that the player cannot see. But ordering the objects in a scene this way, from closest to farthest, is tantamount to solving the VSD problem. Once again, the question is: What can be seen by the player?

由于写入帧缓冲区非常昂贵，理想的渲染器是先绘制离玩家最近的物体，然后是稍远的物体，依此类推，直到屏幕上的每个像素都被写入。到那时，渲染器就知道停止，节省了可能花费在考虑玩家看不到的远处物体上的所有时间。但是，以这种从最近到最远的方式对场景中的物体进行排序等同于解决 VSD 问题。问题再次出现：玩家能看到什么？

Initially, Carmack tried to solve this problem by relying on the layout of Doom’s levels. His renderer started by drawing the walls of the room currently occupied by the player, then flooded out into neighboring rooms to draw the walls in those rooms that could be seen from the current room. Provided that every room was convex, this solved the VSD issue. Rooms that were not convex could be split into convex “sectors.” You can see how this rendering technique might have looked if run at extra-slow speed in this video, where YouTuber Bisqwit demonstrates a renderer of his own that works according to the same general algorithm. This algorithm was successfully used in Duke Nukem 3D, released three years after
Doom, when CPUs were more powerful. But, in 1993, running on the hardware then available, the Doom renderer that used this algorithm struggled with complicated levels—particularly when sectors were nested inside of each other, which was the only way to create something like a circular pit of stairs. A circular pit of stairs led to lots of repeated recursive descents into a sector that had already been drawn, strangling the game engine’s speed.

Around the time that the id team realized that the Doom game engine might be too slow, id Software was asked to port Wolfenstein 3D to the Super Nintendo. The Super Nintendo was even less powerful than the IBM-compatible PCs of the day, and it turned out that the ray-marching Wolfenstein renderer, simple as it was, didn’t run fast enough on the Super Nintendo hardware. So Carmack began looking for a better algorithm. It was actually for the Super Nintendo port of Wolfenstein that Carmack first researched and implemented binary space partitioning. In Wolfenstein, this was relatively straightforward because all the walls were axis-aligned; in Doom, it would be more complex. But Carmack realized that BSP trees would solve Doom’s speed problems too.

最初，卡马克试图依靠《毁灭战士》关卡的布局来解决这个问题。他的渲染器首先绘制玩家当前所在房间的墙壁，然后扩展到相邻房间，绘制从当前房间可以看到的那些房间的墙壁。只要每个房间都是凸形的，这就解决了 VSD 问题。非凸形的房间可以被分割成凸形的 “扇区”。在这个视频中，YouTuber Bisqwit 展示了一个按照相同通用算法工作的渲染器，你可以看到如果以极慢的速度运行，这种渲染技术可能是什么样子。这种算法在《毁灭公爵 3D》（Duke Nukem 3D）中成功使用，它在《毁灭战士》发布三年后推出，当时 CPU 更强大了。但是，在 1993 年，在当时可用的硬件上运行时，使用这种算法的《毁灭战士》渲染器在处理复杂关卡时遇到了困难 —— 特别是当扇区相互嵌套时，这是创建圆形楼梯坑等场景的唯一方法。一个圆形楼梯坑会导致大量重复递归进入已经绘制过的扇区，从而严重影响游戏引擎的速度。

大约在 id 团队意识到《毁灭战士》游戏引擎可能太慢的时候，id Software 被要求将《德军总部 3D》移植到超级任天堂（Super Nintendo）上。超级任天堂比当时的 IBM 兼容 PC 性能更弱，结果发现简单的光线投射《德军总部》渲染器在超级任天堂硬件上运行速度不够快。所以卡马克开始寻找更好的算法。实际上，正是为了《德军总部 3D》的超级任天堂移植版，卡马克首次研究并实现了二叉空间分割。在《德军总部》中，这相对简单，因为所有的墙壁都是轴向对齐的；在《毁灭战士》中，情况会更复杂。但卡马克意识到 BSP 树也能解决《毁灭战士》的速度问题。

Binary Space Partitioning 二叉空间分割

Binary space partitioning makes the VSD problem easier to solve by splitting a 3D scene into parts ahead of time. For now, you just need to grasp why splitting a scene is useful: If you draw a line (really a plane in 3D) across your scene, and you know which side of the line the player or camera viewpoint is on, then you also know that nothing on the other side of the line can obstruct something on the viewpoint’s side of the line. If you repeat this process many times, you end up with a 3D scene split into many sections, which wouldn’t be an improvement on the original scene except now you know more about how different parts of the scene can obstruct each other.

二叉空间分割通过提前将 3D 场景分割成多个部分，使 VSD 问题更容易解决。目前，你只需要理解为什么分割场景是有用的：如果你在你的场景中画一条线（实际上在 3D 中是一个平面），并且你知道玩家或相机视角在这条线的哪一侧，那么你也知道线的另一侧的任何东西都不能遮挡视角这一侧的东西。如果你多次重复这个过程，你最终会得到一个被分割成许多部分的 3D 场景，这对原始场景来说并没有改进，除了现在你更了解场景的不同部分是如何相互遮挡的。

The first people to write about dividing a 3D scene like this were researchers trying to establish for the US Air Force whether computer graphics were sufficiently advanced to use in flight simulators. They released their findings in a 1969 report called “Study for Applying Computer-Generated Images to Visual Simulation.” The report concluded that computer graphics could be used to train pilots, but also warned that the implementation would be complicated by the VSD problem:
One of the most significant problems that must be faced in the real-time computation of images is the priority, or hidden-line, problem. In our everyday visual perception of our surroundings, it is a problem that nature solves with trivial ease; a point of an opaque object obscures all other points that lie along the same line of sight and are more distant. In the computer, the task is formidable. The computations required to resolve priority in the general case grow exponentially with the complexity of the environment, and soon they surpass the computing load associated with finding the perspective images of the objects.

最早写下像这样分割 3D 场景的是为美国空军研究计算机图形是否足够先进以用于飞行模拟器的研究人员。他们在 1969 年的一份名为《计算机生成图像应用于视觉模拟的研究》的报告中公布了他们的发现。该报告得出结论，计算机图形可以用于训练飞行员，但也警告说，VSD 问题会使实施变得复杂：
在图像的实时计算中必须面对的最重要问题之一是优先级或隐藏线问题。在我们日常对周围环境的视觉感知中，这是一个大自然轻松解决的问题；一个不透明物体的一个点会遮挡同一视线中更远的所有其他点。在计算机中，这个任务是艰巨的。在一般情况下，解决优先级所需的计算量随着环境的复杂性呈指数增长，很快就会超过寻找物体透视图像所需的计算负载。

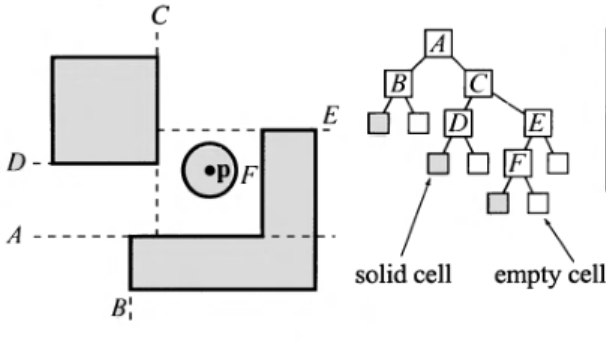
One solution these researchers mention, which according to them was earlier used in a project for NASA, is based on creating what I am going to call an “occlusion matrix.” The researchers point out that a plane dividing a scene in two can be used to resolve “any priority conflict” between objects on opposite sides of the plane. In general you might have to add these planes explicitly to your scene, but with certain kinds of geometry you can just rely on the faces of the objects you already have. They give the example in the figure below, where
p1, p2, and p3 are the separating planes. If the camera viewpoint is on the forward or “true” side of one of these planes, then pi evaluates to 1. The matrix shows the relationships between the three objects based on the three dividing planes and the location of the camera viewpoint—if object ai obscures object aj, then entry aij in the matrix will be a 1.

这些研究人员提到的一种解决方案，据他们说，这种方案早些时候在 NASA 的一个项目中使用过，是基于创建一个我称之为 “遮挡矩阵” 的东西。研究人员指出，将场景一分为二的平面可以用来解决平面两侧物体之间的 “任何优先级冲突”。一般来说，你可能需要将这些平面明确地添加到你的场景中，但对于某些几何形状，你可以仅仅依靠你已经拥有的物体的面。他们给出了下面图中的例子，其中 p1、p2 和 p3 是分隔平面。如果相机视角在这些平面中的一个的前面或 “真实” 一侧，那么 pi 的值为 1。该矩阵根据三个分隔平面和相机视角的位置显示了三个物体之间的关系 —— 如果物体 ai 遮挡了物体 aj，那么矩阵中的条目 aij 将为 1。

The researchers propose that this matrix could be implemented in hardware and re-evaluated every frame. Basically the matrix would act as a big switch or a kind of pre-built z-buffer. When drawing a given object, no video would be output for the parts of the object when a 1 exists in the object’s column and the corresponding row object is also being drawn.

研究人员建议这个矩阵可以在硬件中实现，并在每一帧重新评估。基本上，这个矩阵将充当一个大开关或一种预构建的 z 缓冲区。当绘制给定物体时，如果物体列中有 1 且相应行的物体也正在绘制，则该物体的相应部分不会输出视频。

The major drawback with this matrix approach is that to represent a scene with n objects you need a matrix of size n2. So the researchers go on to explore whether it would be feasible to represent the occlusion matrix as a “priority list” instead, which would only be of size n and would establish an order in which objects should be drawn. They immediately note that for certain scenes like the one in the figure above no ordering can be made (since there is an occlusion cycle), so they spend a lot of time laying out the mathematical distinction between “proper” and “improper” scenes. Eventually they conclude that, at least for “proper” scenes—and it should be easy enough for a scene designer to avoid “improper” cases—a priority list could be generated. But they leave the list generation as an exercise for the reader. It seems the primary contribution of this 1969 study was to point out that it should be possible to use partitioning planes to order objects in a scene for rendering, at least in theory.

这种矩阵方法的主要缺点是，要表示一个有 n 个物体的场景，你需要一个大小为 n² 的矩阵。所以研究人员继续探索是否可以用一个 “优先级列表” 来表示遮挡矩阵，这个列表的大小仅为 n，并确定物体绘制的顺序。他们立即注意到，对于某些场景，如上图中的场景，无法进行排序（因为存在遮挡循环），所以他们花了很多时间阐述 “合适” 和 “不合适” 场景之间的数学区别。最终他们得出结论，至少对于 “合适” 的场景 —— 而且场景设计师应该很容易避免 “不合适” 的情况 —— 可以生成一个优先级列表。但他们把列表的生成留给读者作为练习。似乎 1969 年这项研究的主要贡献是指出，至少在理论上，应该可以使用分割平面来为渲染对场景中的物体进行排序。

It was not until 1980 that a paper, titled “On Visible Surface Generation by A Priori Tree Structures,” demonstrated a concrete algorithm to accomplish this. The 1980 paper, written by Henry Fuchs, Zvi Kedem, and Bruce Naylor, introduced the BSP tree. The authors say that their novel data structure is “an alternative solution to an approach first utilized a decade ago but due to a few difficulties, not widely exploited”—here referring to the approach taken in the 1969 Air Force study. A BSP tree, once constructed, can easily be used to provide a priority ordering for objects in the scene.

直到 1980 年，一篇题为《基于先验树结构的可视表面生成》的论文展示了实现这一目标的具体算法。1980 年由亨利・富克斯（Henry Fuchs）、兹维・凯德姆（Zvi Kedem）和布鲁斯・内勒（Bruce Naylor）撰写的这篇论文介绍了 BSP 树。作者们说，他们的新型数据结构是 “十年前首次使用但由于一些困难未被广泛利用的方法的替代解决方案”—— 这里指的是 1969 年空军研究中采用的方法。一旦构建了 BSP 树，就可以很容易地用于为场景中的物体提供优先级排序。

Fuchs, Kedem, and Naylor give a pretty readable explanation of how a BSP tree works, but let me see if I can provide a less formal but more concise one.
You begin by picking one polygon in your scene and making the plane in which the polygon lies your partitioning plane. That one polygon also ends up as the root node in your tree. The remaining polygons in your scene will be on one side or the other of your root partitioning plane. The polygons on the “forward” side or in the “forward” half-space of your plane end up in the left subtree of your root node, while the polygons on the “back” side or in the “back” half-space of your plane end up in the right subtree. You then repeat this process recursively, picking a polygon from your left and right subtrees to be the new partitioning planes for their respective half-spaces, which generates further half-spaces and further sub-trees. You stop when you run out of polygons.

富克斯、凯德姆和内勒对 BSP 树的工作原理给出了相当易读的解释，但让我看看是否能提供一个不那么正式但更简洁的解释。
首先在你的场景中选择一个多边形，并将该多边形所在的平面作为分割平面。那个多边形也会成为你树的根节点。场景中剩余的多边形将位于根分割平面的一侧或另一侧。平面 “前面” 或 “前半空间” 的多边形最终会在根节点的左子树中，而平面 “后面” 或 “后半空间” 的多边形最终会在根节点的右子树中。然后你递归地重复这个过程，从左子树和右子树中选择一个多边形作为它们各自半空间的新分割平面，这会产生更多的半空间和更多的子树。当你用完多边形时就停止。

Say you want to render the geometry in your scene from back-to-front. (This is known as the “painter’s algorithm,” since it means that polygons further from the camera will get drawn over by polygons closer to the camera, producing a correct rendering.) To achieve this, all you have to do is an in-order traversal of the BSP tree, where the decision to render the left or right subtree of any node first is determined by whether the camera viewpoint is in either the forward or back half-space relative to the partitioning plane associated with the node. So at each node in the tree, you render all the polygons on the “far” side of the plane first, then the polygon in the partitioning plane, then all the polygons on the “near” side of the plane—”far” and “near” being relative to the camera viewpoint. This solves the VSD problem because, as we learned several paragraphs back, the polygons on the far side of the partitioning plane cannot obstruct anything on the near side.

假设你想从后到前渲染场景中的几何图形。（这被称为 “画家算法”，因为这意味着离相机更远的多边形会被离相机更近的多边形覆盖，从而产生正确的渲染效果。）要实现这一点，你所要做的就是对 BSP 树进行中序遍历，在遍历过程中，首先渲染任何节点的左子树还是右子树取决于相机视角相对于与该节点相关的分割平面是在前半空间还是后半空间。所以在树的每个节点上，你首先渲染平面 “远” 侧的所有多边形，然后是分割平面上的多边形，然后是平面 “近” 侧的所有多边形 ——“远” 和 “近” 是相对于相机视角而言的。这解决了 VSD 问题，因为正如我们在前几段学到的，分割平面远侧的多边形不能遮挡近侧的任何东西。

The following diagram shows the construction and traversal of a BSP tree representing a simple 2D scene. In 2D, the partitioning planes are instead partitioning lines, but the basic idea is the same in a more complicated 3D scene.
下面的图表展示了一个表示简单 2D 场景的 BSP 树的构建和遍历。在 2D 中，分割平面变成了分割线，但在更复杂的 3D 场景中基本思想是相同的。
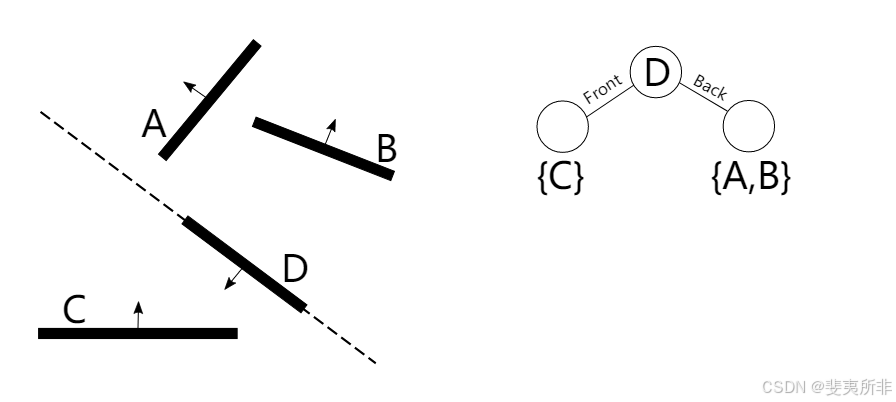
在这里插入图片描述

Step One: The root partitioning line along wall D splits the remaining geometry into two sets.
第一步：沿墙 D 的根分区线将剩余的几何图形分成两组。
在这里插入图片描述

Step Two: The half-spaces on either side of D are split again. Wall C is the only wall in its half-space so no split is needed. Wall B forms the new partitioning line in its half-space. Wall A must be split into two walls since it crosses the partitioning line.

第二步：D 两侧的半空间再次被分割。墙 C 是其半空间中唯一的墙，所以不需要分割。墙 B 在其半空间中形成新的分割线。墙 A 因为穿过分割线必须被分成两部分。

在这里插入图片描述

A back-to-front ordering of the walls relative to the viewpoint in the top-right corner, useful for implementing the painter’s algorithm. This is just an in-order traversal of the tree.

相对于右上角视角，墙的从后到前的顺序，这对于实现画家算法很有用。这只是树的有序遍历。

The really neat thing about a BSP tree, which Fuchs, Kedem, and Naylor stress several times, is that it only has to be constructed once. This is somewhat surprising, but the same BSP tree can be used to render a scene no matter where the camera viewpoint is. The BSP tree remains valid as long as the polygons in the scene don’t move. This is why the BSP tree is so useful for real-time rendering—all the hard work that goes into constructing the tree can be done beforehand rather than during rendering.

富克斯、凯德姆和内勒多次强调，BSP 树的一个非常巧妙之处在于它只需要构建一次。这有点令人惊讶，但无论相机视角在哪里，同一个 BSP 树都可以用于渲染场景。只要场景中的多边形不移动，BSP 树就保持有效。这就是为什么 BSP 树对于实时渲染如此有用 —— 构建树的所有艰苦工作都可以提前完成，而不是在渲染期间进行。

One issue that Fuchs, Kedem, and Naylor say needs further exploration is the question of what makes a “good” BSP tree. The quality of your BSP tree will depend on which polygons you decide to use to establish your partitioning planes. I skipped over this earlier, but if you partition using a plane that intersects other polygons, then in order for the BSP algorithm to work, you have to split the intersected polygons in two, so that one part can go in one half-space and the other part in the other half-space. If this happens a lot, then building a BSP tree will dramatically increase the number of polygons in your scene.

富克斯、凯德姆和内勒说需要进一步探索的一个问题是，什么才是一个 “好” 的 BSP 树。你的 BSP 树的质量将取决于你决定用哪些多边形来确定你的分割平面。我之前跳过了这一点，但是如果你使用一个与其他多边形相交的平面进行分割，那么为了使 BSP 算法起作用，你必须将相交的多边形一分为二，以便一部分可以在一个半空间，另一部分在另一个半空间。如果这种情况经常发生，那么构建 BSP 树将会极大地增加场景中的多边形数量。

Bruce Naylor, one of the authors of the 1980 paper, would later write about this problem in his 1993 paper, “Constructing Good Partitioning Trees.” According to John Romero, one of Carmack’s fellow id Software co-founders, this paper was one of the papers that Carmack read when he was trying to implement BSP trees in Doom.

1980 年那篇论文的作者之一布鲁斯・内勒（Bruce Naylor）后来在他 1993 年的论文《构建良好的分割树》（Constructing Good Partitioning Trees）中谈到了这个问题。据约翰・罗梅罗（John Romero）说，他是卡马克在 id Software 的联合创始人之一，这篇论文是卡马克在《毁灭战士》中尝试实现 BSP 树时阅读的论文之一。

BSP Trees in Doom 《毁灭战士》中的 BSP 树

Remember that, in his first draft of the Doom renderer, Carmack had been trying to establish a rendering order for level geometry by “flooding” the renderer out from the player’s current room into neighboring rooms. BSP trees were a better way to establish this ordering because they avoided the issue where the renderer found itself visiting the same room (or sector) multiple times, wasting CPU cycles.

还记得在《毁灭战士》渲染器的初稿中，卡马克曾试图通过从玩家当前房间向相邻房间 “扩散” 渲染器来确定关卡几何图形的渲染顺序。BSP 树是确定这种顺序的更好方法，因为它们避免了渲染器多次访问同一个房间（或扇区）从而浪费 CPU 周期的问题。

“Adding BSP trees to Doom” meant, in practice, adding a BSP tree generator to the Doom level editor. When a level in Doom was complete, a BSP tree was generated from the level geometry. According to Fabien Sanglard, the generation process could take as long as eight seconds for a single level and 11 minutes for all the levels in the original Doom. The generation process was lengthy in part because Carmack’s BSP generation algorithm tries to search for a “good” BSP tree using various heuristics. An eight - second delay would have been unforgivable at runtime, but it was not long to wait when done offline, especially considering the performance gains the BSP trees brought to the renderer. The generated BSP tree for a single level would have then ended up as part of the level data loaded into the game when it starts.

在实践中，“在《毁灭战士》中添加 BSP 树” 意味着在《毁灭战士》关卡编辑器中添加一个 BSP 树生成器。当《毁灭战士》中的一个关卡完成时，会根据关卡几何图形生成一个 BSP 树。据法比安・桑格拉德（Fabien Sanglard）说，单个关卡的生成过程可能需要长达八秒，而原始《毁灭战士》的所有关卡则需要 11 分钟。生成过程之所以漫长，部分原因是卡马克的 BSP 生成算法试图使用各种启发式方法寻找一个 “好” 的 BSP 树。在运行时，八秒的延迟是不可原谅的，但离线完成时等待时间并不长，特别是考虑到 BSP 树给渲染器带来的性能提升。单个关卡生成的 BSP 树随后会作为关卡数据的一部分在游戏启动时加载。

Carmack put a spin on the BSP tree algorithm outlined in the 1980 paper, because once Doom is started and the BSP tree for the current level is read into memory, the renderer uses the BSP tree to draw objects front - to - back rather than back - to - front. In the 1980 paper, Fuchs, Kedem, and Naylor show how a BSP tree can be used to implement the back - to - front painter’s algorithm, but the painter’s algorithm involves a lot of over - drawing that would have been expensive on an IBM - compatible PC. So the Doom renderer instead starts with the geometry closer to the player, draws that first, then draws the geometry farther away. This reverse ordering is easy to achieve using a BSP tree, since you can just make the opposite traversal decision at each node in the tree. To ensure that the farther - away geometry is not drawn over the closer geometry, the Doom renderer uses a kind of implicit z - buffer that provides much of the benefit of a z - buffer with a much smaller memory footprint. There is one array that keeps track of occlusion in the horizontal dimension, and another two arrays that keep track of occlusion in the vertical dimension from the top and bottom of the screen. The Doom renderer can get away with not using an actual z - buffer because Doom is not technically a fully 3D game. The cheaper data structures work because certain things never appear in Doom: The horizontal occlusion array works because there are no sloping walls, and the vertical occlusion arrays work because no walls have, say, two windows, one above the other.

卡马克对 1980 年论文中概述的 BSP 树算法进行了改进，因为一旦《毁灭战士》启动并将当前关卡的 BSP 树读入内存，渲染器就会使用 BSP 树从前到后而不是从后到前绘制物体。在 1980 年的论文中，富克斯、凯德姆和内勒展示了如何使用 BSP 树实现从后到前的画家算法，但画家算法涉及大量的重绘，在 IBM 兼容 PC 上成本很高。因此，《毁灭战士》渲染器改为从离玩家更近的几何图形开始，先绘制它，然后再绘制更远的几何图形。使用 BSP 树很容易实现这种相反的顺序，因为你可以在树的每个节点上做出相反的遍历决策。为了确保较远的几何图形不会覆盖较近的几何图形，《毁灭战士》渲染器使用了一种隐式 z 缓冲区，它提供了 z 缓冲区的大部分好处，但内存占用要小得多。有一个数组用于跟踪水平方向的遮挡，另外两个数组分别从屏幕顶部和底部跟踪垂直方向的遮挡。《毁灭战士》渲染器可以不使用实际的 z 缓冲区，因为从技术上讲，《毁灭战士》并不是一个完全的 3D 游戏。这些更简单的数据结构之所以有效，是因为某些东西在《毁灭战士》中从未出现过：水平遮挡数组有效是因为没有倾斜的墙壁，垂直遮挡数组有效是因为没有墙壁上有比如说上下排列的两个窗户。

The only other tricky issue left is how to incorporate Doom’s moving characters into the static level geometry drawn with the aid of the BSP tree. The enemies in Doom cannot be a part of the BSP tree because they move; the BSP tree only works for geometry that never moves. So the Doom renderer draws the static level geometry first, keeping track of the segments of the screen that were drawn to (with yet another memory-efficient data structure). It then draws the enemies in back - to - front order, clipping them against the segments of the screen that occlude them. This process is not as optimal as rendering using the BSP tree, but because there are usually fewer enemies visible than there is level geometry in a level, speed isn’t as much of an issue here.

剩下的唯一棘手问题是如何将《毁灭战士》中的移动角色融入到借助 BSP 树绘制的静态关卡几何图形中。《毁灭战士》中的敌人不能成为 BSP 树的一部分，因为它们会移动；BSP 树只适用于从不移动的几何图形。所以《毁灭战士》渲染器先绘制静态关卡几何图形，跟踪已绘制的屏幕部分（使用另一种内存高效的数据结构）。然后它以从后到前的顺序绘制敌人，将它们与遮挡它们的屏幕部分进行裁剪。这个过程不如使用 BSP 树进行渲染那么理想，但由于通常一个关卡中可见的敌人比关卡几何图形少，所以速度在这里不是一个大问题。

Using BSP trees in Doom was a major win. Obviously it is pretty neat that Carmack was able to figure out that BSP trees were the perfect solution to his problem. But was it a genius-level move?

在《毁灭战士》中使用 BSP 树是一个重大的成功。显然，卡马克能够发现 BSP 树是解决他问题的完美方案是相当了不起的。但这是一个天才级别的举动吗？

In his excellent book about the Doom game engine, Fabien Sanglard quotes John Romero saying that Bruce Naylor’s paper, “Constructing Good Partitioning Trees,” was mostly about using BSP trees to cull backfaces from 3D models. According to Romero, Carmack thought the algorithm could still be useful for Doom, so he went ahead and implemented it. This description is quite flattering to Carmack—it implies he saw that BSP trees could be useful for real-time video games when other people were still using the technique to render static scenes. There is a similarly flattering story in Masters of Doom: Kushner suggests that Carmack read Naylor’s paper and asked himself, “what if you could use a BSP to create not just one 3D image but an entire virtual world?”

在他关于《毁灭战士》游戏引擎的优秀著作中，法比安・桑格拉德引用约翰・罗梅罗的话说，布鲁斯・内勒的论文《构建良好的分割树》主要是关于使用 BSP 树从 3D 模型中剔除背面。据罗梅罗说，卡马克认为这个算法对《毁灭战士》仍然有用，所以他着手实施了它。这个描述对卡马克相当恭维 —— 它暗示当其他人还在使用该技术渲染静态场景时，他就看到了 BSP 树对实时视频游戏的用处。《毁灭战士大师》中也有一个类似的恭维故事：库什纳暗示卡马克读了内勒的论文后问自己：“如果你能用 BSP 树创建的不仅仅是一个 3D 图像，而是一整个虚拟世界呢？”

This framing ignores the history of the BSP tree. When those US Air Force researchers first realized that partitioning a scene might help speed up rendering, they were interested in speeding up real-time rendering, because they were, after all, trying to create a flight simulator. The flight simulator example comes up again in the 1980 BSP paper. Fuchs, Kedem, and Naylor talk about how a BSP tree would be useful in a flight simulator that pilots use to practice landing at the same airport over and over again. Since the airport geometry never changes, the BSP tree can be generated just once. Clearly what they have in mind is a real-time simulation. In the introduction to their paper, they even motivate their research by talking about how real-time graphics systems must be able to create an image in at least 1/30th of a second.

这种说法忽略了 BSP 树的历史。当那些美国空军研究人员最初意识到分割场景可能有助于加速渲染时，他们感兴趣的是加速实时渲染，因为毕竟他们试图创建一个飞行模拟器。飞行模拟器的例子在 1980 年的 BSP 论文中再次出现。富克斯、凯德姆和内勒谈到了 BSP 树在飞行员反复练习在同一机场降落的飞行模拟器中会有多么有用。由于机场的几何形状从不改变，BSP 树可以只生成一次。显然，他们想到的是实时模拟。在他们论文的引言中，他们甚至通过谈论实时图形系统必须能够在至少 1/30 秒内创建一个图像来为他们的研究提供动机。

So Carmack was not the first person to think of using BSP trees in a real-time graphics simulation. Of course, it’s one thing to anticipate that BSP trees might be used this way and another thing to actually do it. But even in the implementation Carmack may have had more guidance than is commonly assumed. The Wikipedia page about BSP trees, at least as of this writing, suggests that Carmack consulted a 1991 paper by Chen and Gordon as well as a 1990 textbook called Computer Graphics: Principles and Practice. Though no citation is provided for this claim, it is probably true. The 1991 Chen and Gordon paper outlines a front - to - back rendering approach using BSP trees that is basically the same approach taken by Doom, right down to what I’ve called the “implicit z - buffer” data structure that prevents farther polygons being drawn over nearer polygons. The textbook provides a great overview of BSP trees and some pseudocode both for building a tree and for displaying one. (I’ve been able to skim through the 1990 edition thanks to my wonderful university library.) Computer Graphics: Principles and Practice is a classic text in computer graphics, so Carmack might well have owned it.

所以卡马克不是第一个想到在实时图形模拟中使用 BSP 树的人。当然，预见到 BSP 树可能会以这种方式使用是一回事，实际去做又是另一回事。但即使在实施过程中，卡马克可能也比通常认为的有更多的指导。维基百科上关于 BSP 树的页面（至少在撰写本文时）表明，卡马克参考了陈和戈登 1991 年的一篇论文以及一本 1990 年的教科书《计算机图形学：原理与实践》。虽然没有为这个说法提供引用，但它很可能是真的。1991 年陈和戈登的论文概述了一种使用 BSP 树的从前到后的渲染方法，这与《毁灭战士》所采用的方法基本相同，甚至包括我所说的防止较远多边形覆盖较近多边形的 “隐式 z 缓冲区” 数据结构。这本教科书对 BSP 树进行了很好的概述，并提供了构建树和显示树的一些伪代码。（多亏了我出色的大学图书馆，我能够浏览 1990 年版。）《计算机图形学：原理与实践》是计算机图形学的经典教材，所以卡马克很可能拥有它。

Still, Carmack found himself faced with a novel problem—”How can we make a first-person shooter run on a computer with a CPU that can’t even do floating-point operations?”—did his research, and proved that BSP trees are a useful data structure for real-time video games. I still think that is an impressive feat, even if the BSP tree had first been invented a decade prior and was pretty well theorized by the time Carmack read about it. Perhaps the accomplishment that we should really celebrate is the Doom game engine as a whole, which is a seriously nifty piece of work. I’ve mentioned it once already, but Fabien Sanglard’s book about the Doom game engine (Game Engine Black Book: DOOM) is an excellent overview of all the different clever components of the game engine and how they fit together. We shouldn’t forget that the VSD problem was just one of many problems that Carmack had to solve to make the Doom engine work. That he was able, on top of everything else, to read about and implement a complicated data structure unknown to most programmers speaks volumes about his technical expertise and his drive to perfect his craft.

尽管如此，卡马克面临着一个新的问题 ——“我们如何让一个第一人称射击游戏在一台甚至不能进行浮点运算的计算机上运行？”—— 他进行了研究，并证明了 BSP 树是实时视频游戏的一种有用的数据结构。我仍然认为这是一项令人印象深刻的壮举，即使 BSP 树在十年前就已经被发明出来，并且在卡马克读到它的时候已经有了相当完善的理论。也许我们真正应该庆祝的成就是整个《毁灭战士》游戏引擎，这是一件非常精巧的作品。我已经提到过一次，但是法比安・桑格拉德关于《毁灭战士》游戏引擎的书（《游戏引擎黑皮书：毁灭战士》）是对游戏引擎所有不同的巧妙组件以及它们如何协同工作的一个极好的概述。我们不应忘记，可视表面判定问题只是卡马克为了使《毁灭战士》引擎工作而必须解决的众多问题之一。他能够在解决其他所有问题的基础上，阅读并实现一种大多数程序员都不知道的复杂数据结构，这充分说明了他的技术专长和追求技艺完美的动力。

Ref

Michael Abrash, “Michael Abrash’s Graphics Programming Black Book,” James Gregory, accessed November 6, 2019, http://www.jagregory.com/abrash-black-book/#chapter-64-quakes-visible-surface-determination.
R. Schumacher, B. Brand, M. Gilliland, W. Sharp, “Study for Applying Computer-Generated Images to Visual Simulation,” Air Force Human Resources Laboratory, December 1969, accessed on November 6, 2019, https://apps.dtic.mil/dtic/tr/fulltext/u2/700375.pdf.
Henry Fuchs, Zvi Kedem, Bruce Naylor, “On Visible Surface Generation By A Priori Tree Structures,” ACM SIGGRAPH Computer Graphics, July 1980.
Fabien Sanglard, Game Engine Black Book: DOOM (CreateSpace Independent Publishing Platform, 2018), 200.
Sanglard, 206.
Sanglard, 200.
David Kushner, Masters of Doom (Random House Trade Paperbacks, 2004), 142.

[图形学] 简化的 BSP 树

ZJU_fish1996 于 2016-09-16 15:43:43 发布

简介

BSP 树是一种空间分割树，它主要用于游戏中的场景管理，尤其是室内场景的管理。

它的本质是二叉树，也就是用一个面把空间分割成两部分，分割出的空间则继续用面分割，以此类推，直到到达特定递归深度，或者空间中不再有物体或只剩下一个物体（得到凸包 / 凸多面体）。

最终，叶结点对应场景中的物体，内部结点存储分割面。物体被 “收纳” 到各个包围盒中。

应用

BSP 树对应的应用主要有两个方面：

(1) 确定物体的遮挡关系，可视化处理。

(2) 碰撞检测的广阶段。

首先，要明确的一点是， BSP 树是在设计地图时自动生成的树，它随之被保存到磁盘，也就是事先进行了预处理。在加载场景的时候，我们直接读入 bsp 文件，而不是重新生成。

这也就意味着，作为预处理技术， BSP 树只能处理静态的场景。

BSP 树本身的结构非常简单，但是这并不代表着 BSP 树的编程非常容易。其复杂性主要体现在：

(1) BSP 树不是独立存在的，它需要与前期的地图编辑器和后期的场景剔除 / 碰撞检测结合在一起。而这两者都是非常复杂的项目。

(2) 选择合适的分割面，使得树尽可能平衡，并且能在恰当的时候停止分割。

对于场景剔除而言，重点就是判断物体的前后关系，而这种空间拓扑关系在 BSP 树中已有了明显的体现。我们从根结点开始，根据摄像机所在位置和分割平面进行对比，很容易就能判断出结点的两个子空间与视点的前后关系。我们认为与视点在同一侧的为前面，在不同侧的为后面。

对于碰撞检测而言，对所有物体都两两进行碰撞检测十分耗时，我们可以首先对物体进行初步排查，如果不处在同一个叶结点（包围盒），那么一定不会发生碰撞，通过简单的遍历树避免了繁琐的计算。

具体实现

BSP 树的编程比较复杂，在这里对 BSP 树做了最简化。之后的代码仅作为练习用，目的是更好地掌握 BSP 树。

如果希望学习可用于商业引擎的 BSP 树，可参考 quake3 的地图编辑器。

主要参考了《实时渲染》一书中给出的一个 BSP 结构，如下：

简化部分：

(1) 使用二维，而不是三维。

(2) 手工输入包围盒，而不是自动生成。包围盒为 AABB 包围盒（轴向），不支持上图中的凹多边形。

(3) 叶结点和内部结点共用一个数据结构。其中内部结点存储了方向（水平或竖直）以及分割线；叶结点存储了对应场景为实心还是空心。

(4) 沿着包围盒的边界进行分割（和图中所示相同），选择分割线的方法比较简单：

分别选出水平和竖直方向的最优分割线。（判断标准：与空间中心最接近的包围盒边界线）
如果最优水平分割线和场景中物体相交，而最优竖直分割线和场景中物体不相交，那么优先选择最优竖直分割线，反之亦然。

如果都相交或都不相交，那么优先选择距离中心点更近的（按相对比例来算）

如果选择的分割线与包围盒相交，那么把这个包围盒根据分割线拆成两个包围盒。

(5) 退出条件（达到之一）：

达到最大分割层数，直接生成两个叶结点，返回。
空间里没有物体了，返回空叶结点。
空间里只剩下一个物体了，返回满叶结点。

详细介绍已在代码注释中体现。

结点数据结构

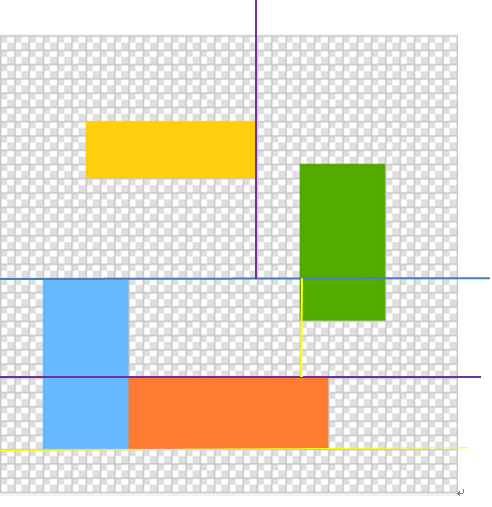
样例

蓝线：第一次分割；紫线：第二次分割；黄线：第三次分割

包围盒：

（4,10,4,16）
（10,24,4,9）
（7,19,23,27）
（22,28,13,24）

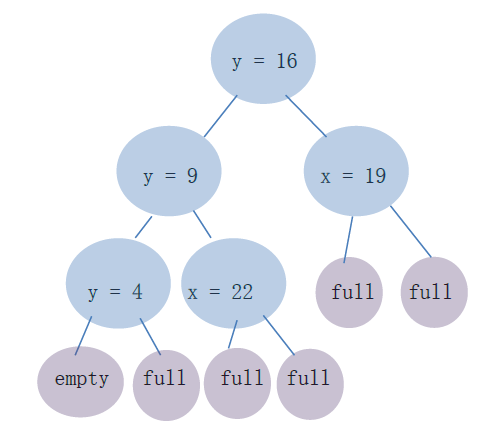
BSP 树

代码

bsp.h

#pragma once
 
#include<vector>
 
class bspTree
{
private:
	struct bspNode {
		bspNode* left;
		bspNode* right;
		bool isLeaf;//是否是叶结点
		bool isSolid;//是否实心
		bool isHori;//是否水平
		float data;//分割线
	};//结点数据结构
	struct box_t {
		float xmin;
		float xmax;
		float ymin;
		float ymax;
		box_t();
		void set(float x1, float x2, float y1, float y2);
	};//包围盒数据结构
	bspNode* root;//根节点
	std::vector<box_t>box;//包围盒容器
	float xmin, xmax, ymin, ymax;//整个场景的轴向包围盒
	int boxNum;//包围盒的个数
	int layer;//树的最大深度
	int layer_count;//记录当前层数
	bspNode* createEmptyNode();//生成空叶结点
	bspNode* createSolidNode();//生成非空叶结点
	void split(float& data_x, float& data_y, float& dis_x, float& dis_y,
		float xmin, float xmax, float ymin, float ymax);//寻找最优分割线
	bspNode* genNode(bool isFull_1, bool isFull_2, int layer_count,
		float xmin, float xmax, float ymin, float ymax, float data,bool isHori);//生成新的结点
	bspNode* build(int layer_count, float xmin, float xmax,
		float ymin, float ymax);//创建新的结点
	bool isIntersect(float xmin, float xmax, float ymin, float ymax, float data, bool isHori,std::vector<int>& id,int& num);
	//某一空间中的分割线是否与空间中的一个包围盒相交
	void traversal(bspNode* t);//前序遍历
	bool inBox(float x1, float x2, float y1, float y2, int id);//包围盒id是否完全处在某个空间中
	void checkIsFull(bool& isFull_x_1, bool& isFull_x_2, bool& isFull_y_1, bool& isFull_y_2,
		float xmin, float xmax, float ymin, float ymax, float data_x, float data_y);//检测分割出的两个区域是否为满/空
	bool isIntersect(float x1, float x2, float y1, float y2, int id);//包围盒id是否与某个空间有交集
public:
	bspTree(float x1, float x2, float y1, float y2, int l);//构造
	//前四个参数为场景包围盒，l为最大递归深度
	void add(float x1, float x2, float y1, float y2);//添加包围盒
	void build();//创建 BSP 树
	void print();//前序遍历输出
	void levelOrder();//层次遍历输出
};

bsp.cpp

#include"bsp.h"
#include<algorithm>
#include<queue>
bspTree::box_t::box_t() { }
void bspTree::box_t::set(float x1, float x2, float y1, float y2)
{
	xmin = x1;
	xmax = x2;
	ymin = y1;
	ymax = y2;
}
bspTree::bspTree(float x1, float x2, float y1, float y2, int l)
{
	xmin = x1;
	xmax = x2;
	ymin = y1;
	ymax = y2;
	layer = l;
	boxNum = 0;
	layer_count = 0;
	root = nullptr;
}
void bspTree::add(float x1, float x2, float y1, float y2)
{
	box_t b;
	boxNum++;
	b.set(x1, x2, y1, y2);
	box.push_back(b);
}

//某一空间中的分割线是否与空间中的一个包围盒相交

bool bspTree::isIntersect(float xmin,float xmax,float ymin,float ymax,float data, bool isHori, std::vector<int>& id,int& num)

{
	bool flag = false;//记录是否存在交
	//分割线是水平的
	if (isHori) {
		//遍历所有包围盒
		for (int i = 0; i < boxNum; i++) {
			//如果包围盒完全处在空间中
			if (inBox(xmin, xmax, ymin, ymax, i)) {
				num++;//记录包围盒个数+1
				if (data > box[i].xmin && data < box[i].xmax) { //存在交
					id.push_back(i);//记录包围盒id
					flag = true;//存在交 为真
				}
			}
		}
	}
	//分割线是竖直的
	else if (!isHori) {
		//遍历所有包围盒
		for (int i = 0; i < boxNum; i++) {
			//如果包围盒完全处在空间中
			if (inBox(xmin, xmax, ymin, ymax, i)) {
				num++;//记录包围盒个数+1
				if(data > box[i].ymin&&data < box[i].ymax) {//存在交
					id.push_back(i);//记录包围盒id
					flag = true;//存在交 为真
		    	}
			}
		}
	}
	return flag;
}
//包围盒id是否完全处在某个空间中
bool bspTree::inBox(float x1, float x2, float y1, float y2,int id)
{
	return box[id].xmin >= x1 && box[id].xmax<=x2 &&
		box[id].ymin>=y1 && box[id].ymax <= y2;
}

//寻找最优分割线

void bspTree::split(float& data_x, float& data_y, float& dis_x, float& dis_y,
	float xmin, float xmax, float ymin, float ymax)
{
	float d = 10000;
	//先计算竖直方向
 
	//遍历所有包围盒
	for (int i = 0; i < boxNum; i++) {
		//如果包围盒完全处在空间中
		if (inBox(xmin,xmax,ymin,ymax,i)) {
			//计算包围盒边界线到中心的距离
			d = box[i].xmin - ((xmax - xmin) / 2 + xmin);
			if (d < 0)d = -d;
			//如果有更小的距离，更新距离和分割线
			if (d < dis_x) {
				dis_x = d;
				data_x = box[i].xmin;
			}
			//计算包围盒边界线到中心的距离
			d = box[i].xmax - ((xmax - xmin) / 2 + xmin);
			if (d < 0) d = -d;
			//如果有更小的距离，更新距离和分割线
			if (d < dis_x) {
				dis_x = d;
				data_x = box[i].xmax;
			}
		}
	}
	//再计算水平方向
	//遍历所有包围盒
	for (int i = 0; i < boxNum; i++) {
		//如果包围盒完全处在空间中
		if (inBox(xmin, xmax, ymin, ymax, i)) {
			//计算包围盒边界线到中心的距离
			d = box[i].ymin - ((ymax - ymin) / 2 + ymin);
			if (d < 0)d = -d;
			//如果有更小的距离，更新距离和分割线
			if (d < dis_y) {
				dis_y = d;
				data_y = box[i].ymin;
			}
			//计算包围盒边界线到中心的距离
			d = box[i].ymax - ((ymax - ymin) / 2 + ymin);
			if (d < 0)d = -d;
			//如果有更小的距离，更新距离和分割线
			if (d < dis_y) {
				dis_y = d ;
				data_y = box[i].ymax;
			}
		}
	}
	//计算相对距离
	dis_x /= xmax - xmin;
	dis_y /= ymax - ymin;
}
//创建空叶结点
bspTree::bspNode* bspTree::createEmptyNode()
{
	bspNode* node = new bspNode();
	node->left = nullptr;
	node->right = nullptr;
	node->isLeaf = true;
	node->isSolid = false;
	node->data = 0.0f;
	return node;
}
//创建非空叶结点
bspTree::bspNode* bspTree::createSolidNode()
{
	bspNode* node = new bspNode();
	node->left = nullptr;
	node->right = nullptr;
	node->isLeaf = true;
	node->isSolid = true;
	node->data = 0.0f;
	return node;
}
 
//生成结点
bspTree::bspNode* bspTree::genNode(bool isFull_1,bool isFull_2,int layer_count,
	float xmin,float xmax,float ymin,float ymax,float data,bool isHori)
{
	bspNode* node = new bspNode();//申请
	if (!root) { //指定根
		root = node;
	}
	//如果没有到达最大的深度
	if (layer != layer_count) {
		//如果区域1是满的
		if (isFull_1) {
			//递归创建
			if(isHori)node->left = build(layer_count + 1,xmin, xmax,ymin,data);
			else node->left = build(layer_count + 1, xmin, data, ymin, ymax);
		}
		//如果区域1是空的
		else {
			//直接创建空叶结点，不继续递归
			node->left = createEmptyNode();
		}
		//如果区域2是满的
		if (isFull_2) {
			//递归创建
			if(isHori)node->right = build(layer_count + 1, xmin, xmax,data,ymax);
			else node->right = build(layer_count + 1, data, xmax, ymin, ymax);
		}
		//如果区域2是空的
		else {
			//直接创建空叶结点，不继续递归
			node->right = createEmptyNode();
		}
	}
	//如果达到了最大深度
	else if (layer ==layer_count) {
		//如果区域1是满的
		if (isFull_1) {
			//直接创建满叶结点，不继续递归
			node->left = createSolidNode();
		}
		//如果区域1是空的
		else {
			//直接创建空叶结点，不继续递归
			node->left = createEmptyNode();
		}
		//如果区域2是满的
		if (isFull_2) {
			//直接创建满叶结点，不继续递归
			node->right = createSolidNode();
		}
		//如果区域2是空的
		else {
			//直接创建空叶结点，不继续递归
			node->right = createEmptyNode();
		}
	}
	//设置结点基本信息
	node->isLeaf = false;
	node->isHori = isHori;
	node->data = data;
	return node;
}

//包围盒id是否与某个空间有交集
bool bspTree::isIntersect(float x1, float x2, float y1, float y2, int id)
{
	//两种情况：
	// 1. 水平，竖直方向都各有至少一条边界线落在区域内（不含恰好落在区域边界）
	// 2. 水平方向两条边界线都落在区域边界，或竖直方向两条边界线都落在区域边界
	return ((box[id].xmin > x1 && box[id].xmin<x2 ||
		box[id].xmax>x1 && box[id].xmax<x2||
		box[id].xmin == x1 && box[id].xmax==x2) &&
		(box[id].ymin>y1&&box[id].ymin<y2 ||
		box[id].ymax>y1&&box[id].ymax < y2)||
		box[id].ymin==y1&&box[id].ymax==y2);
}

//检测分割出的两个区域是否为满/空

void bspTree::checkIsFull(bool& isFull_x_1, bool& isFull_x_2, bool& isFull_y_1, bool& isFull_y_2,
	float xmin, float xmax, float ymin, float ymax,float data_x,float data_y)
{
	//遍历所有包围盒，如果有包围盒与该空间存在交集，那么这个空间就是满的
	for (int i = 0; i < boxNum; i++) {
		if (!isFull_x_1 && isIntersect(xmin, data_x, ymin, ymax,i)) {
			isFull_x_1 = true;
		}
		if (!isFull_x_2 && isIntersect(data_x, xmax, ymin, ymax, i)) {
			isFull_x_2 = true;
		}
		if (!isFull_y_1 && isIntersect(xmin, xmax, ymin, data_y, i)) {
			isFull_y_1 = true;
		}
		if (!isFull_y_2 && isIntersect(xmin, xmax, data_y, ymax, i)) {
			isFull_y_2 = true;
		}
	}
	return;
}
 
//创建 BSP 树
bspTree::bspNode* bspTree::build(int layer_count, float xmin, float xmax,
	float ymin, float ymax)
{
	//printf("%f %f %f %f\n", xmin, xmax, ymin, ymax);
	//超过递归深度直接返回NULL
	if (layer_count == layer + 1)return nullptr;
	bspNode* node = nullptr;
 
	//初始化一些变量：距离，分割线，是否相交，子空间空/满状态，相交包围盒的id，空间内包围盒的个数
	float dis_x = 10000;
	float dis_y = 10000;
	float data_x = -1;
	float data_y = -1;
	bool isIntersect_x;
	bool isIntersect_y;
	bool isFull_x_1 = false;
	bool isFull_x_2 = false;
	bool isFull_y_1 = false;
	bool isFull_y_2 = false;
	std::vector<int>id_x;
	std::vector<int>id_y;
	int num_x = 0;
	int num_y = 0;
 
	split(data_x, data_y, dis_x, dis_y, xmin, xmax, ymin, ymax);//找到预备的最优分裂线
	
	//两者未赋值，说明没有可以选择的包围盒，也就是空间是空的，直接返回空叶节点
	if (data_x == -1 && data_y == -1) {
		return createEmptyNode();
	}
 
	//判断最优分裂线与包围盒是否相交
	isIntersect_x = isIntersect(xmin,xmax,ymin,ymax,data_x, true,id_x,num_x);
	isIntersect_y = isIntersect(xmin,xmax,ymin,ymax,data_y, false,id_y,num_y);
	//判断分割的子空间为空/满
	checkIsFull(isFull_x_1, isFull_x_2, isFull_y_1, isFull_y_2, xmin, xmax, ymin, ymax, data_x, data_y);
	//空间中只有一个物体，直接返回满叶结点
	if (num_x == 1)return createSolidNode();
 
	//竖直分割线相交，水平分割线不相交，选择水平分隔线
	if (isIntersect_x && !isIntersect_y) {
		node = genNode(isFull_y_1, isFull_y_2, layer_count, xmin, xmax, ymin, ymax, data_y,true);
	}
	//竖直分割线不相交，水平分割线相交，选择竖直分隔线
	else if (!isIntersect_x && isIntersect_y) {
		node = genNode(isFull_x_1, isFull_x_2, layer_count, xmin, xmax, ymin, ymax, data_x,false);
	}
	//都相交 或都不相交，选择距离中心近的
	else {
		//竖直更近
		if (dis_x < dis_y) {
			//如果存在相交，分裂包围盒
			if (isIntersect_x) {
				for (int i = 0; i < id_x.size(); i++) {
					float x1 = box[id_x[i]].xmin;
					float x2 = box[id_x[i]].xmax;
					float y1 = box[id_x[i]].ymin;
					float y2 = box[id_x[i]].ymax;
					boxNum++;
					box[id_x[i]].set(x1, data_x, y1, y2);
					box_t b;
					b.set(data_x, x2, y1, y2);
					box.push_back(b);
				}
				id_x.clear();
			}
			node = genNode(isFull_x_1, isFull_x_2, layer_count, xmin, xmax, ymin, ymax, data_x,false);
		}
		//水平更近
		else {
			//如果存在相交，分裂包围盒
			if (isIntersect_y) {
				for (int i = 0; i < id_y.size(); i++) {
					float x1 = box[id_y[i]].xmin;
					float x2 = box[id_y[i]].xmax;
					float y1 = box[id_y[i]].ymin;
					float y2 = box[id_y[i]].ymax;
					boxNum++;
					box[id_y[i]].set(x1, x2, y1, data_y);
					box_t b;
					b.set(x1, x2, data_y, y2);
					box.push_back(b);
				}
				id_y.clear();
			}
			node = genNode(isFull_y_1, isFull_y_2, layer_count, xmin, xmax, ymin, ymax, data_y,true);
		}
	}
	return node;
}
 
//创建入口
void bspTree::build()
{
	build(1, xmin, xmax, ymin, ymax);
}
 
//前序输出
void bspTree::print()
{
	traversal(root);
}
 
//前序
void bspTree::traversal(bspNode* t)
{
	if (!t)return;
	if (t->data != 0)printf("%f ", t->data);
	else printf("leaf:%d", t->isSolid);
	if (t->isHori)printf("h\n");
	else printf("v\n");
	traversal(t->left);
	traversal(t->right);
}

//层序
void bspTree::levelOrder()
{
	std::queue<bspNode*>q;
	q.push(root);
	while (!q.empty()) {
		bspNode* t = q.front();
		if(t->data!=0)printf("%f ", t->data);
		else printf("leaf:%d", t->isSolid);
		if (t->isHori)printf("h\n");
		else printf("v\n");
		q.pop();
		if (t->left != nullptr)q.push(t->left);
		if (t->right != nullptr)q.push(t->right);
	}
	return;
}

main.cpp

#include "bsp.h"
#include<stdlib.h>
int main()
{
	bspTree* t = new bspTree(1,33,1,33,3);
	t->add(4, 10, 4, 16);
	t->add(10, 24, 4, 9);
	t->add(7, 19, 23, 27);
	t->add(22, 28, 13, 24);
	t->build();
	t->print();
	printf("\n");
	t->levelOrder();
	system("pause");
}

BSP Tree 算法简述

packdge_black于 2021-03-13 15:49:51 发布

一、前言

什么是 BSP 树？

In computer science, binary space partitioning (BSP) is a method for recursively subdividing a space into two convex sets by using hyperplanes as partitions. This process of subdividing gives rise to a representation of objects within the space in the form of a tree data structure known as a BSP tree.

BSP 树的应用场景

performing geometrical operations with shapes (constructive solid geometry) in CAD,（碰撞检测）collision detection in robotics and 3D video games,ray tracing(光线追踪)，and other applications that involve the handling of complex spatial scenes.

BSP 树的来源

Fuchs，Kedem和Naylor 在 1980 年左右引入了二进制空间分区树（或简称 BSP 树）。并有两篇发布的论文：“Predeterming Visibility Priority in 3-D Scenes” 和 “On Visible Surface Generation by A Priori Tree Structures”，讲述了 BSP 树的实用性和如何实现它们。后来也有作者，在这两篇论文的基础上，结合了阴影的生成和动态场景的处理。

简单来说， BSP 树是n维空间到凸子空间的分层细分（a BSP tree is a heirarchical subdivisions of n dimensional space into convex subspaces）。每个节点都有一个前叶子节点和后叶子节点。从根节点开始，所有后续插入都由当前节点的超平面划分。在二维空间中，超平面是一条线。在 3 维空间中，超平面是一个平面。 BSP 树的最终目标是让叶节点的超平面在父节点超平面的前面或后面（这句可能翻译不太好，我把原句放上来：The end goal of a BSP tree if for the hyperplanes of the leaf nodes to be trivially “behind” or “infront” of the parent hyperplane.）

BSP 树对于与静态图像的显示进行实时交互非常有用。在渲染静态场景之前，需要计算 BSP 树。可以非常快地（线性时间）遍历 BSP 树，以去除隐藏的表面和投射阴影。通过一些工作，可以修改 BSP 树以处理场景中的动态事件。

下图展示了 BSP Tree对一个立方体的分割，其中最小的单元为立方体 mesh 的每一个面：

二、 BSP 树的构造过程

下面是在对象空间构建 BSP 树的过程

1、首先，选择一个分区超平面。为了方便讨论，我们将使用一个二维世界，而我们的根节点将是一条线。

2、使用初始分区超平面对世界上的所有多边形进行分区，并将它们存储在正面或背面多边形列表中。(Partition all polygons in the world with the initial partition hyperplane, storing them in either the front or back polygon list.)

3、在前后多边形列表中进行递归或迭代，创建一个新的树节点，并将其附加到父节点的左侧或右侧叶子。(recurse or iterate through the front and back polygon list, creating a new tree node and attaching it the the left or right leaf of the parent node.)

根节点的选择将直接影响树的大小。如果根节点跨越许多不同的多边形，则可能会生成一棵大树。

由于计算 BSP 树通常是在渲染之前完成的，因此找到最佳根节点的最简单方法是测试少量候选对象。应该选择导致 BSP 树中的节点数最少的节点.

当多边形或直线被超平面划分(when a polygon or line is partitioned by the hyperplane)时，有四种情况需要处理：

polygon is in-front of hyperplane
polygon is behind hyperlane
polygon is coincident with the hyperplane
polygon spans the hyperplane

对于前两种情况，仅将线或面添加到树的适当节点。如果线或面重合，则可以通过将多个面存储在 BSP 树的节点中来进行处理。如果多边形跨越超平面，则多边形分割算法必须找到多边形与平面的交点。这可以通过凸多边形的射线平面相交方法来完成。

最后， BSP 树算法可以递归或迭代地执行。递归 BSP 树非常易于理解，因为它仅基于当前的超平面执行分区，然后递归前后叶节点。下面的示例代码对此进行了说明：

bsp_tree(poly* current_poly)
{
  while(still_polygons)
  {
     partition_polygons(current_poly);
   }
bsp_tree(current_poly->left);
bsp_tree(current_poly->right);
}

但是，出于性能原因，递归并不总是很吸引人。在大多数情况下， BSP 树计算是在交互渲染场景之前完成的。但是，如果将动态对象插入树中，则可能需要实时进行 BSP 树计算。

或者，递归可以由堆栈建模。当您想遍历 BSP 树时，将节点的指针推到堆栈上。

BSP 树的示例创建

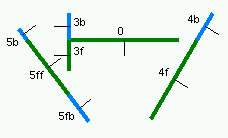
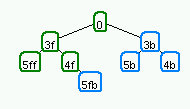
为了真正了解 BSP 树的工作原理，查看树创建的图形演示可能会有所帮助。以下图像集显示了如何在二维示例中将行添加到 BSP 树。

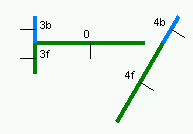
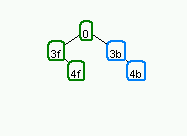
首先，创建一个根节点和分区平面。

首先，创建一个根节点和分区平面。	显然根没有任何节点.

二、 BSP 树的应用

1、使用BSP渲染场景

改善渲染性能是使用 BSP 树的原因之一。 BSP 树本质上执行了从后到前的 painters 算法或从前到后的扫描线算法的大量预计算。可以从任意角度以线性时间遍历树。

由于 painters 算法的工作原理是先绘制距离眼睛最远的多边形，因此以下代码递归到树的底部并绘制多边形。随着递归的展开，距离眼睛较近的多边形会绘制在较远的多边形上。因为 BSP 树已经准备好将多边形拆分为小块，所以 painters 算法中最难的部分已经准备好解决。

code for back to front tree traversal.

traverse_tree(bsp_tree* tree,point eye)
{
location = tree->find_location(eye);
 
if(tree->empty())
  return;
 
 
  if(location > 0)      // if eye infront of location
  {
    traverse_tree(tree->back,eye);
    display(tree->polygon_list);
    traverse_tree(tree->front,eye);
  }
  else if(location < 0) // eye behind location
  {
    traverse_tree(tree->front,eye);
    display(tree->polygon_list);
    travers_tree(tree->back,eye);
  }
  else                  // eye coincidental with partition hyperplane
  {
    traverse_tree(tree->front,eye);
    traverse_tree(tree->back,eye);
  }
}

使用 BSP 树生成阴影：

虽然 BSP 树可用于在静态场景中快速去除隐藏表面，但它们也可用于计算具有一个或多个固定光源的阴影。传统的阴影生成方法是从点光源发出的两个向量和对象边缘的顶点形成阴影多边形。将阴影体积裁剪到视图体积（屏幕，地板，墙壁等）上以创建有限的体积。阴影多边形内的任何多边形都在阴影中。针对场景多边形和视点之间的阴影多边形的相对数量测试了场景多边形上的所有可见点，以确定该点是否在阴影中。

上面的方法需要两遍：一遍构建阴影体积，另一遍对阴影多边形进行测试。还必须通过光源的透视变换来变换场景。大多数阴影体积方法需要剪切多边形，而不是像 BSP 方法中那样剪切平面。

Chin 和 Feiner 提出的 “阴影体积 BSP 树” 算法 (The Shadow Volume BSP Tree algorithm) 不需要裁剪视图体积或场景的任何形式的变换。基本上，SVBSP 方法会在将多边形插入 BSP 树的过程中创建合并的阴影体积。只要场景和光源是静态的，就可以预先计算 SVBSP。

SV BSP 树算法在每个内部节点处都有一个影子平面。阴影平面由点光源和多边形的边缘定义。平面法线的方向确定对象是否在阴影中或阴影之外。

SVBSP 算法有两个主要步骤：

Determining shadows:

将多边形过滤掉 SV BSP 树，以确定它是亮还是暗。如果该多边形同时处于阴影和光照下，则将其分为两个多边形。请注意，如果一个多边形位于眼睛前面，并且其阴影体积已由更靠近光源的多边形定义，则可以丢弃较远的多边形。在将行 ef 添加到 SV BSP 树中的示例中可以看到这一点。

Enlarging the SVBSP tree：

一旦通过 SV BSP 树过滤了多边形，就将计算其阴影体积并将其插入树中。在分段的情况下（例如，在下面的示例中），阴影体积已在另一个阴影体积内，并且不需要包含在内。

文献来源：

【1】https://en.wikipedia.org/wiki/Binary_space_partitioning

【2】https://web.cs.wpi.edu/~matt/courses/cs563/talks/bsp/document.html

【3】https://physicsforanimators.com/what-is-a-bsp-tree/

【4】https://xiaoyp.github.io/2019/11/24/BSP-Net

BSP 树的简单理解和二叉树空间索引思路的详解

酱香拿钢已于 2023-02-21 16:33:04 修改

BSP 树

二叉空间分区树（Binary Space Partioning Tree，BSP Tree）也叫二叉空间分割树，简称 BSP 树

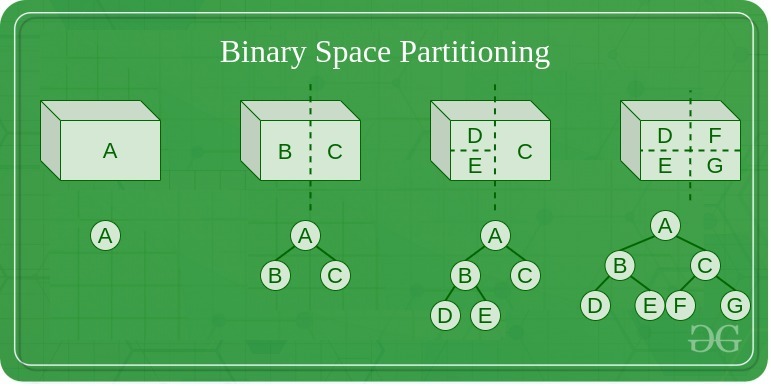
从多边形列表生成 BSP 树的算法

从列表中选择一个多边形 P。
在 BSP 树中创建一个节点 N，并将 P 添加到该节点的多边形列表中。
对于列表中的其他多边形：
如果该多边形完全位于包含 P 的平面前面，请将该多边形移动到 P 前面的节点列表中。
如果该多边形完全位于包含 P 的平面后面，请将该多边形移动到 P 后面的节点列表中。
如果该多边形与包含 P 的平面相交，则将其拆分为两个多边形，并将它们移动到 P 后面和前面的相应多边形列表中。
如果该多边形位于包含 P 的平面中，请将其添加到节点 N 处的多边形列表中。
将此算法应用于 P 前面的多边形列表。
将此算法应用于 P 后面的多边形列表。

BSP 的缺点

生成 BSP 树可能非常耗时。
BSP 不能解决可见表面测定的问题。

BSP 的用途

它用于 3D 视频游戏和机器人中的碰撞检测。
它用于光线追踪
它涉及复杂空间场景的处理。

k-d 树

二叉树空间索引思路

直觉

给定一堆已有的样本数据，和一个被询问的数据点（红色五角星），我们如何找到离五角星最近的 15 个点？

先忽略在编程上的实现，想一想一个人如何主观地执行。嗯，他一定会把在五角附近的一些点中，分别计算每一个的距离，然后选最近的 15 个。这样可能只需要进行二三十次距离计算，而不是 300 次。

如图，只对紫圈里的点进行计算。

啊哈！问题来了。我们讲到的 “附近” 已经包含了距离的概念，如果不经过计算我们怎么知道哪个点是在五角星的 “附近”？为什么我们一下就认出了 “附近” 而计算机做不到？那是因为我们在观看这张图片时，得到的输入是已经带有距离概念的影像，然而计算机在进行计算时得到的则是没有距离概念的坐标数据。如果要让一个人人为地从 300 组坐标里选出最近的 15 个，而不给他图像，那么他也省不了功夫，必须要把 300 个全部计算一遍才行。

这样来说，我们要做的就是在干巴巴的坐标数据上进行加工，将空间分割成小块，并以合理地方法将信息进行储存，这样方便我们读取 “附近” 的点。

切割

这只危险的兔子，它又回来了！它今天上了四个纹身，爱心、月牙、星星和眼泪，下面是它的照片。

我们来回答一个简单的问题：在这幅照片上，距离爱心最近的纹身是什么？

在这个问题中，每个纹身的特征是照片平面上的横轴和竖轴的坐标。

对于这个问题，如果进行蛮算的办法我们需要计算 3 次距离（分别和月亮、眼泪和星星算一次）。下面我们要做的是把整个空间按照左右和上下进行等分，并且把分割后的小空间以二叉树形式进行记录，这样可以很快地读取邻近的点而省去计算量。

好，我们先竖向沿中间把这个兔子切成两半

再沿横向从中间切成四份

再沿着竖向平分八份

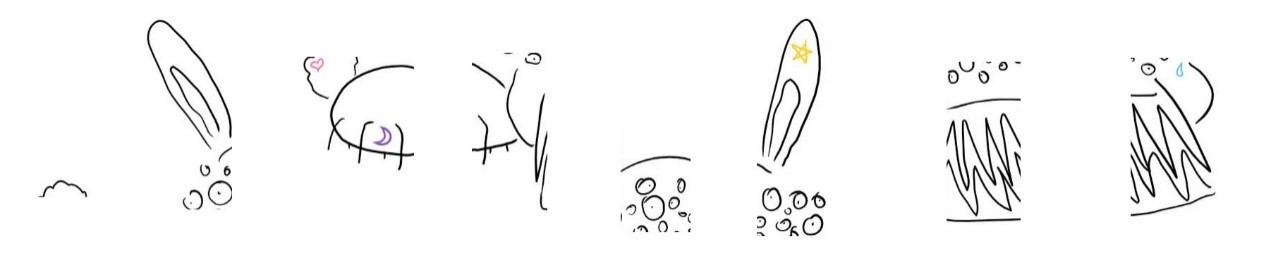
最后再沿横向切一次。这次有些区域是完全空白的，我们就把它舍弃不要了，得到 14 份：

我们再按照上下左右的关系把切开的图片做成一个二叉树，树的每一个节点是一幅图，它的两个枝是这幅图平分出来的子图。

可以看出这个树状结构包含了很多局部性的信息，因为它的每一个节点都是按照上下或者左右进行平分的，因此如果两个点在树中的距离较近，那么它们的实际距离就是比较近的。

搜寻

接下来我们要通过这棵二叉树找到离爱心最近的纹身。

首先从树的最顶端开始，向下搜寻找到最底部包含爱心的节点。这个操作非常简单，因为每一次分割要么是沿着某纵线 x=a 要么是沿着横线 y=a，因此只需要判断爱心的 x 或 y 轴坐标是大于 a 还是小于 a，便知道是向左还是右边选择树枝。

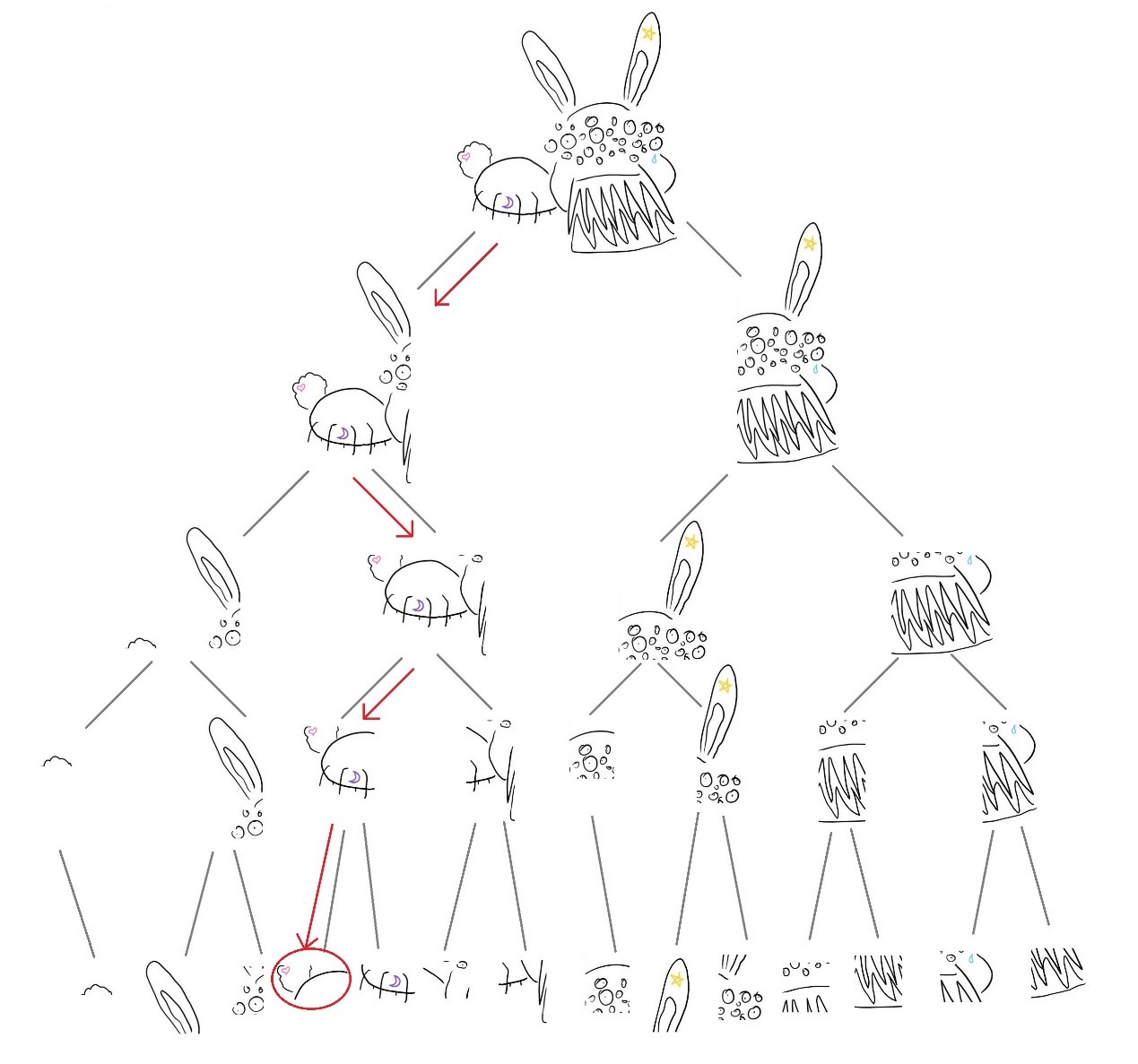
在找到了爱心之后，我们沿着相同的路径向上攀爬。只爬了一节就发现了屁股上的两个纹身

这里看出，在 8 平分的情况下，爱心和月亮是在同一个区域的。在某种意义上来讲它们是 “近” 的，但是我们还不能确定它们是最近的，因此还要继续向上攀爬寻找。再继续向上爬两个节点，都没有出现爱心和月亮以外的纹身。在下面这个节点中

我们发现爱心和月亮之间的距离（红线）要小于爱心和分割线的距离（蓝线），也就是说，不论分割线的右边是什么情况，那边的纹身都不可能离爱心更近。因此可以判断，离爱心最近的图形是月亮。

这样，我们只计算了一次爱心和月亮之间的距离和一次爱心和分割线之间的距离，而不是分别计算爱心和其他三个纹身的距离。并且，要知道，爱心和分割线之间距离的计算非常简单，就是爱心的 x 坐标和分割线的 x 坐标的差（的绝对值），相比于计算两点之间的距离要省下很多计算量。

麻烦

啊，但也有可能这个搜寻最近点的过程没那么顺利。在上面的计算中，在找到了离爱心比较近的月亮之后，我们发现爱心距离分割线的距离比较远，因此确定月亮的确就是最近的。但是，在分割线的另一边有一个更近的纹身，那么情况就稍微复杂了。

就说这个兔子啊，又去加了两个纹身，一片叶子和一个圆圈。

二叉树分割上也相应地多出这两个纹身。我们想找到离爱心最近的纹身，所以依旧向下搜寻先找到爱心。

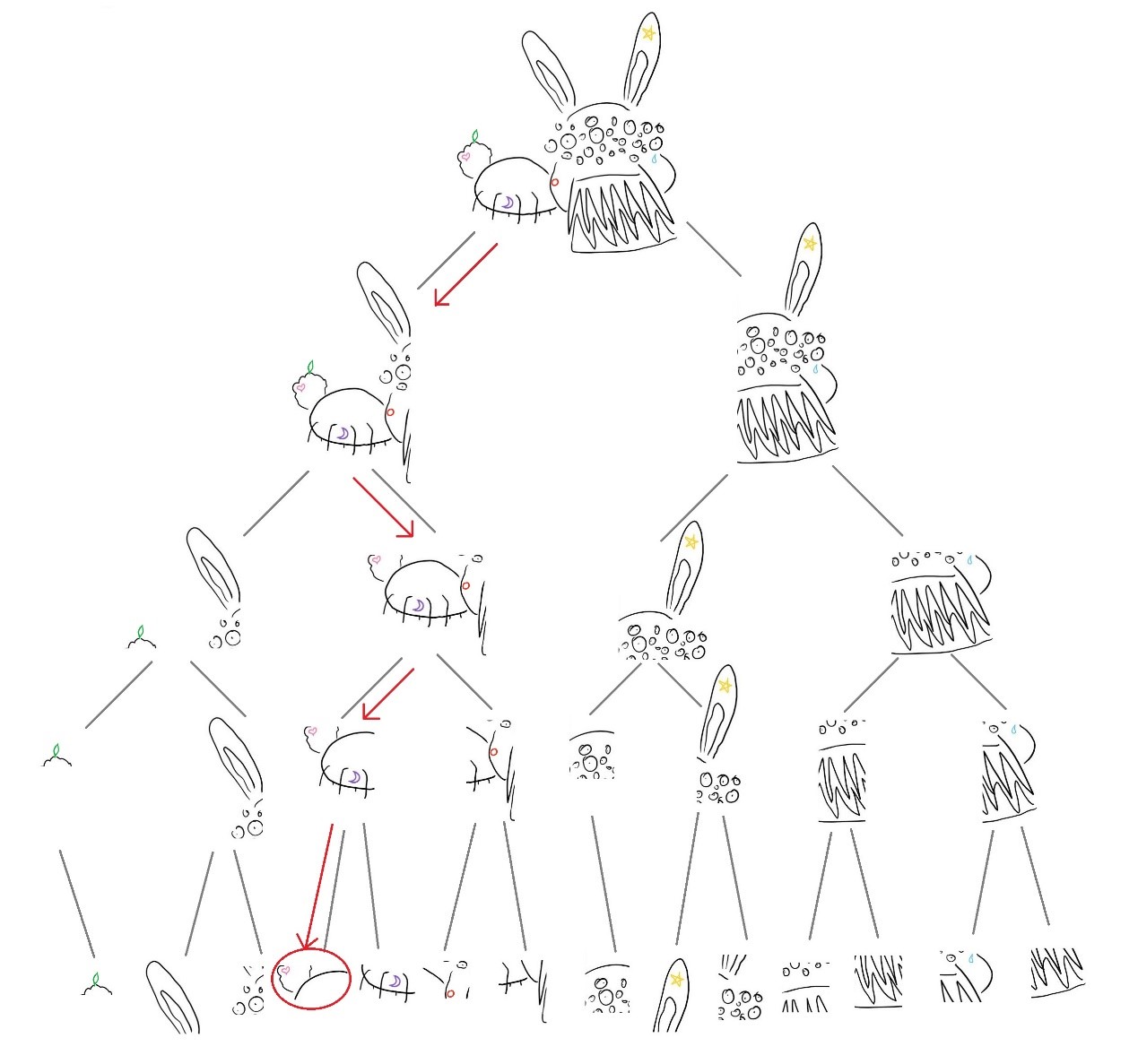
我们找来一张纸，记下在已访问节点中距离爱心最近的纹身和所对应的距离。现在这张纸还是空的。

向上爬了一节，发现那一节的另一个枝里有月亮，于是跑下去查看月亮的坐标，计算爱心和月亮的距离，并在纸上记录 (图形=月亮，距离=d1)(图形=月亮，距离=�1)。

再回到蓝圈的节点向上爬，继续向上爬。我们发现，d1�1（红线）大于爱心和分割线的距离（蓝线）。

也就是说分割线的另一边可能有更近的点，所以从另一个分枝开始向下搜，找到…

在另一个分枝中我们追溯到圆圈，并计算它与爱心的距离 d2，发现 d2>d1，比月亮远，所以丢弃不要。

再向上爬一个节，我们发现 d1（红线）大于爱心和切分线之间的距离（蓝线）

因此，切分线的另一端可能有更近的纹身，因此我们从另一个树枝向下搜索…

找到了叶子。（所幸在这个分枝里只搜索到了叶子，如果有更多的图形的话，还需要进行多层的递归。具体的过程会在后面的详细篇中讲解。）计算叶子和爱心之间的距离，得 d3，并发现 d3<d1，比月亮更近，于是更新纸上的记录为 (纹身=叶子，距离=d3)。

再向上攀登一节，我们发现 d3小于爱心和切分线的距离，因此另一边的数据就不用考虑了。

这次我们已经爬到了树的最顶端，完成了搜索，纸上记载的 (叶子，d3) 就是最近的纹身和对应的距离。

结语

在以上的算法中，当我们已经找到了比切分线更近的点时，就不需要继续搜索切分线另一边的点了，因为那些只会更远。于是，通过把整个空间进行分割并以树状结构进行记录，我们只需要在问题点附近的一些区域进行搜寻便可以找到最近的数据点，节省了大量的计算。

–

via：

How Much of a Genius-Level Move Was Using Binary Space Partitioning in Doom? 06 Nov 2019
https://twobithistory.org/2019/11/06/doom-bsp.html
[图形学] 简化的 BSP 树-CSDN博客 ZJU_fish1996 于 2016-09-16 15:43:43 发布
https://blog.csdn.net/ZJU_fish1996/article/details/52554620
BSP Tree 算法简述-CSDN博客 packdge_black于 2021-03-13 15:49:51 发布
https://blog.csdn.net/packdge_black/article/details/114681992
BSP 树的简单理解和二叉树空间索引思路的详解-CSDN博客 酱香拿钢已于 2023-02-21 16:33:04 修改
https://blog.csdn.net/weixin_43925768/article/details/129138298