漫话:为什么计算机中 0.2 + 0.1 不等于 0.3 ?
原创 漫话编程





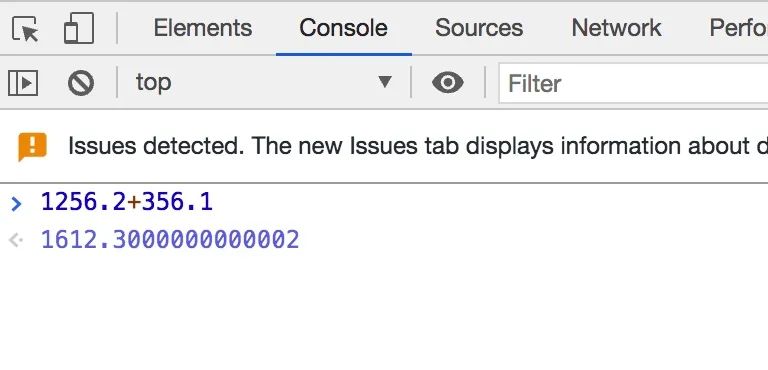


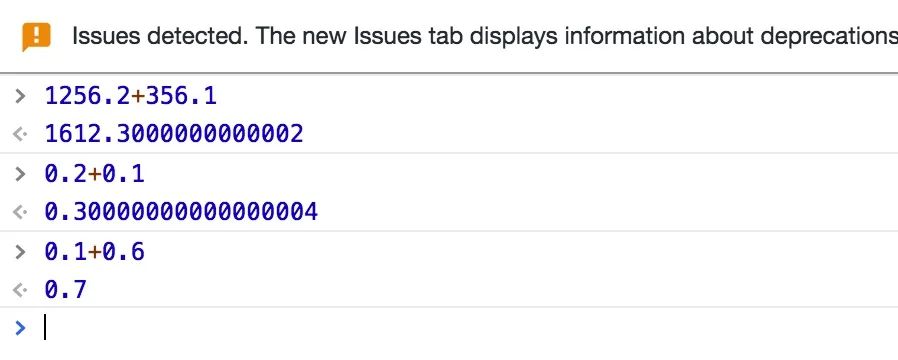


为什么当我们使用电脑浏览器计算 0.2+0.1 的时候,解决却是 0.30000000000000004,而 0.1+0.6 的结果却是 0.7 呢?
这个问题其实一直是一个经典的问题,甚至有一个网站的域名就是 https://0.30000000000000004.com ,主要就是解释这个问题的。
在这个网站中,列举了各种编程语言中计算 0.2+0.1 的结果,摘选几个如下:

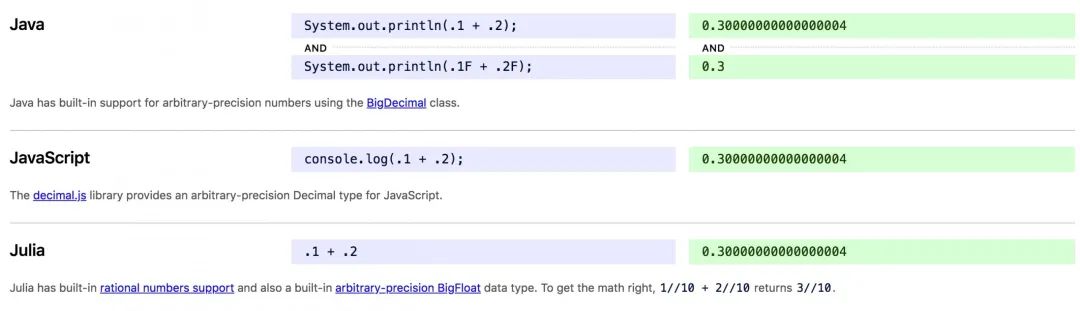
可以看到,在各种语言中,计算 0.2+0.1 的结果都出奇的一致,那就是这个神奇的 0.30000000000000004。
其实,当我们使用浏览器的控制台F12进行计算的时候,用到的就是 JavaScript语言进行计算的,所以,前面的现象,归根结底其实与具体的编程语言无关。
主要问题还是计算机中到底是如何表示小数以及如何进行小数运算的。


我们知道,计算机只认识 0 和 1,现实世界中的内容想要通过计算机存储、计算或者展示,都需要转换 2 进制。在现实世界中,数字主要有整数和小数两种。
计算机中表示整数的方式有很多,如原码、反码以及补码等。
整数包括正整数、负整数以及零。在计算机中存储的整数则分为有符号数和无符号数。
对于无符号数,采用哪种编码方式都无所谓,对于有符号数的编码方式,常用的是补码。
那么,一个十进制数字想要获得其二进制的补码,需要先通过一定的算法得到他对应的原码。


十进制转二进制
首先我们看一下,如何把十进制整数转换成二进制整数?
十进制整数转换为二进制整数采用 “除 2 取余,逆序排列” 法。
具体做法是:
- 用 2 整除十进制整数,可以得到一个商和余数;
- 再用 2 去除商,又会得到一个商和余数,如此进行,直到商为小于 1 时为止
- 然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。
如,我们想要把 127 转换成二进制,做法如下:

那么,十进制小数转换成二进制小数,又该如何计算呢?
十进制小数转换成二进制小数采用 “乘 2 取整,顺序排列” 法。
具体做法是:* 用 2 乘十进制小数,可以得到积 * 将积的整数部分取出,再用 2 乘余下的小数部分,又得到一个积 * 再将积的整数部分取出,如此进行,直到积中的小数部分为零,此时 0 或 1 为二进制的最后一位。或者达到所要求的精度为止。

所以,十进制的 0.625 对应的二进制就是 0.101。


不是所有数都能用二进制表示
我们知道了如何将一个十进制小数转换成二进制,那么是不是计算就可以直接用二进制表示小数了呢?
前面我们的例子中 0.625 是一个特列,那么还是用同样的算法,请计算下 0.1 对应的二进制是多少?
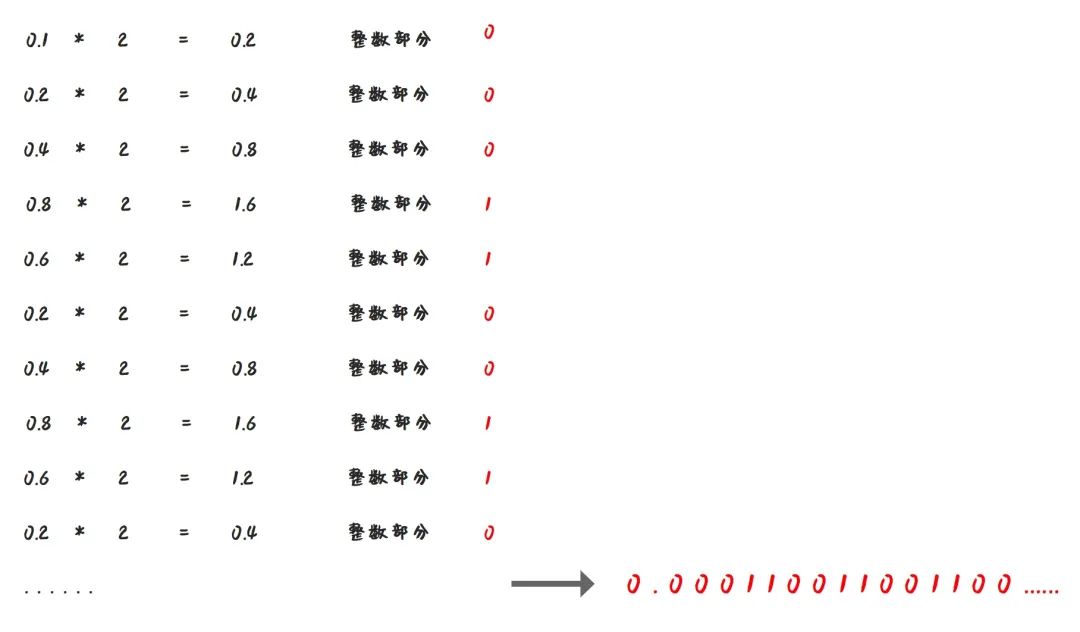
我们发现,0.1 的二进制表示中出现了无限循环的情况,也就是 (0.1) 10 = (0.000110011001100…) 2
这种情况,计算机就没办法用二进制精确的表示 0.1 了。
也就是说,对于像 0.1 这种数字,我们是没办法将他转换成一个确定的二进制数的。




IEEE 754
为了解决部分小数无法使用二进制精确表示的问题,于是就有了 IEEE 754 规范。
IEEE 二进制浮点数算术标准(IEEE 754)是 20 世纪 80 年代以来最广泛使用的浮点数运算标准,为许多 CPU 与浮点运算器所采用。
浮点数和小数并不是完全一样的,计算机中小数的表示法,其实有定点和浮点两种。因为在位数相同的情况下,定点数的表示范围要比浮点数小。所以在计算机科学中,使用浮点数来表示实数的近似值。
IEEE 754 规定了四种表示浮点数值的方式:单精确度(32 位)、双精确度(64 位)、延伸单精确度(43 比特以上,很少使用)与延伸双精确度(79 比特以上,通常以 80 位实现)。
其中最常用的就是 32 位单精度浮点数和 64 位双精度浮点数。
IEEE 并没有解决小数无法精确表示的问题,只是提出了一种使用近似值表示小数的方式,并且引入了精度的概念。
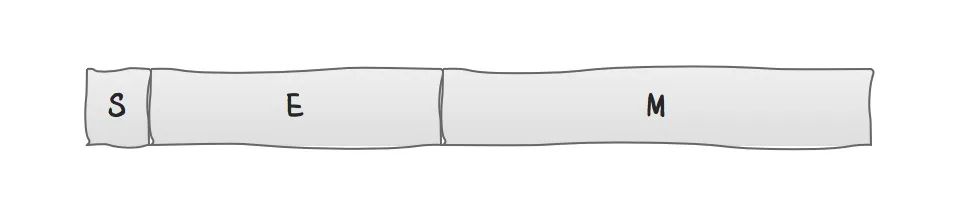
浮点数是一串 0 和 1 构成的位序列 (bit sequence),从逻辑上用三元组 { S , E , M } \{S, E, M\} {S,E,M} 表示一个数 N N N。
如下图所示:
-
S (sign) 表示浮点数 N N N 的符号位。对应值 s s s 满足:
- 当 n > 0 n > 0 n>0 时, s = 0 s = 0 s=0
- 当 n ≤ 0 n \leq 0 n≤0 时, s = 1 s = 1 s=1
-
E (exponent) 表示浮点数 N N N 的指数位,位于符号位 S S S 和尾数位 M M M 之间的若干位。对应值 e e e 可以是正数或负数。
-
M (mantissa) 表示浮点数 N N N 的尾数位,恰好位于浮点数的末尾。 M M M 也被称作有效数字位 (significand)、系数位 (coefficient),甚至被称作 “小数”。
因此,浮点数 N N N 的实际值 n n n 由下方的公式表示:
n = ( − 1 ) s × m × 2 e \displaystyle \Large n=\mathop{(-1)}^{s}\times m\times \mathop{2}^{e} n=(−1)s×m×2e
上面这个公式看起来很复杂,其中符号位和尾数位还比较容易理解,但是这个指数位就不是那么容易理解了。
其实,大家也不用太过于纠结这个公式,大家只需要知道对于单精度浮点数,最多只能用 32 位字符表示一个数字,双精度浮点数最多只能用 64 位来表示一个数字。
而对于那些无限循环的二进制数来说,计算机采用浮点数的方式保留了一定的有效数字,那么这个值只能是近似值,不可能是真实值。
至于一个数对应的 IEEE 754 浮点数应该如何计算,不是本文的重点,这里就不再赘述了,过程还是比较复杂的,需要进行对阶、尾数求和、规格化、舍入以及溢出判断等。
但是这些其实不需要了解的太详细,我们只需要知道,小数在计算机中的表示是近似数,并不是真实值。根据精度不同,近似程度也有所不同。
如小数 0.1,对应的在双精度浮点数的二进制为:
0.00011001100110011001100110011001100110011001100110011001
小数 0.2
0.00110011001100110011001100110011001100110011001100110011
两者相加:
0.1: 0.00011001100110011001100110011001100110011001100110011001
+
0.2: 0.00110011001100110011001100110011001100110011001100110011
------------------------------
0.01001100110011001100110011001100110011001100110011001101

转换成 10 进制之后得到:0.30000000000000004




避免精度丢失
在 Java 中,使用 float 表示单精度浮点数,double 表示双精度浮点数,表示的都是近似值。
所以,在 Java 代码中,千万不要使用 float 或者 double 来进行高精度运算,尤其是金额运算,否则就很容易产生资损问题。
为了解决这样的精度问题,Java 中提供了 BigDecimal 来进行精确运算。




参考资料:
https://0.30000000000000004.com/
https://zh.wikipedia.org/zh-hans/IEEE_754
https://www.h-schmidt.net/FloatConverter/IEEE754.html
一个神奇的网站 0.30000000000000004.co
原创 胡译胡说
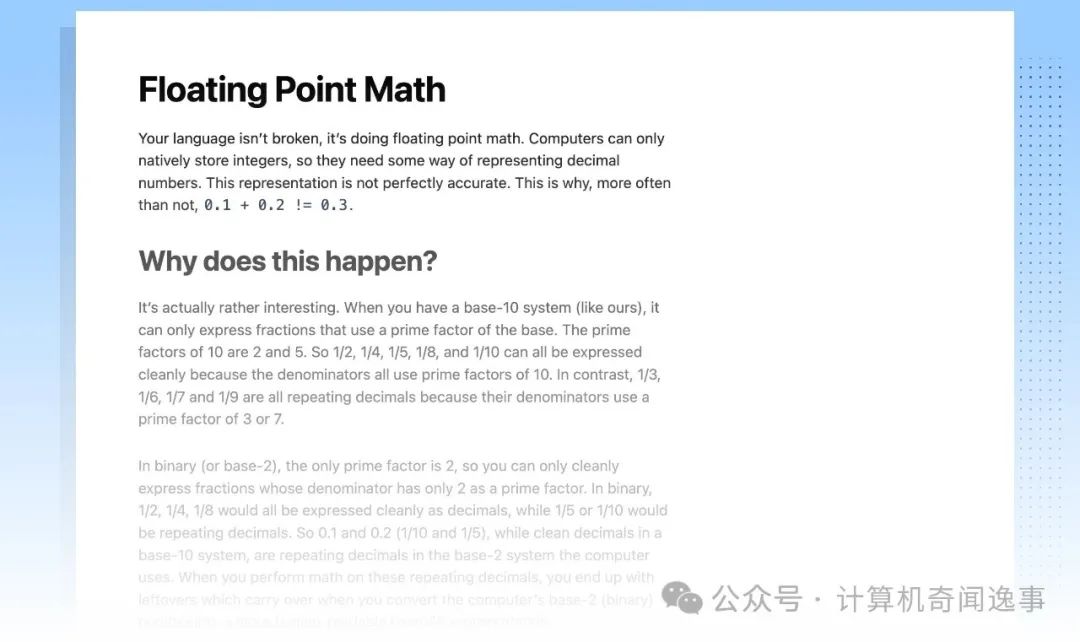
在计算 0.1 + 0.2 = 时,计算机(编程语言)给出的结果往往是 0.30000000000000004,而不是 0.3。
这一现象源于小数在计算机中的表示方式不同于常用的十进制表示方式。由此产生的差异经常导致人们误解,认为精密的计算机连这样简单的算术运算都会算错。
于是,一名叫作 Erik Wiffin 的工程师制作了 0.30000000000000004.com 这个网站,用于解释计算机为什么不能 “正确” 计算 0.1 + 0.2。
有意思的是,这个域名既不好记忆又容易输错,但若利用连 0.3 都能算“错”的编程语言,却能轻松打开。
例如,我们可以在浏览器开发者工具的控制台中执行如下代码:
window.location = `https://${0.1 + 0.2}.com`
window.location// 获取或设置当前窗口的 URL
https://${0.1 + 0.2}.com//${}内的表达式会被计算并替换为结果
都知道 0.1+0.2 = 0.30000000000000004,那要怎么让它等于 0.3
文 / 初见雨夜
2022-04-02

前言
小学数学老师教过我们,0.1 + 0.2 = 0.3,但是为什么在我们在浏览器的控制台中输出却是 0.30000000000000004?
除了加法有这个奇怪的现象,带小数点的减法和乘除计算也会得出意料之外的结果
console.log(0.3 - 0.1) // 0.19999999999999998
console.log(0.1 * 0.2) // 0.020000000000000004
console.log(0.3 / 0.1) // 2.9999999999999996
原因
我们都知道计算机时是通过二进制来进行计算的,即 0 和 1
就拿 0.1 + 0.2 来说,0.1表示为0.0001100110011001...,而0.2表示为0.0011001100110011...
而在二进制中 1 + 1 = 10,所以 0.1 + 0.2 = 0.0100110011001100...
转成10进制就近似表示为 0.30000000000000004
结论
简单来说就是,浮点数转成二进制时丢失了精度,因此在二进制计算完再转回十进制时可能会和理论结果不同
对于浮点数的四则运算,许多编程语言都会有理论值和实际值不同的问题。例如Java中也会出现类似的问题,但是Java中可以使用java.math.BigDecimal类来避免这种情况
可是JS是弱类型的语言,作者Brendan Eich自述10天内开发出JS语言,一开始设计的时候就没有对浮点数计算有个处理的好方法
那么在日常开发的前端项目中我们可以怎么解决嘞?
解决方案
简单实现
使用toFixed()<不推荐>
可以控制小数点后几位,如果为空的话会用0补充,返回一个字符串
> 0.123.toFixed(2) // '0.12'
缺点:
- 在不同浏览器中得出的值可能不相同,且部分数字得不到预计的结果,并不是执行严格的四舍五入
// 在chrome控制台中
> 1.014.toFixed(2) // '1.01'
> 1.215.toFixed(2) // '1.22'
> 1.105.toFixed(2) // '1.10'
> 1.115.toFixed(2) // '1.11'
乘以一个10的幂次方
把需要计算的数字乘以10的n次方,让数值都变为整数,计算完后再除以10的n次方,这样就不会出现浮点数精度丢失问题
> (0.1 * 10 + 0.2 *10) / 10 // 0.3
我们可以将它封装成一个函数
mathFloat = function (float, digit) {
const math = Math.pow(10, digit);
return parseInt(float * math, 10) / math;
}
mathFloat(0.1 + 0.2, 3) // 0.3
缺点:
-
JS中的存储都是通过8字节的 double 浮点类型表示的,因此它并不能准确记录所有数字,它存在一个数值范围
Number.MAX_SAFE_INTEGER为 9007199254740991,而 Number.MIN_SAFE_INTEGER为 -9007199254740991,超出这个范围的话JS是无法表示的
虽然范围有限制,但是数值一般都够用
较为完整的实现
加法
function mathPlus(arg1, arg2) {
let r1, r2, m;
try {
r1 = arg1.toString().split(".")[1].length; // 获取小数点后字符长度
} catch (error) {
r1 = 0; // 为整数状态,r1赋0
}
try {
r2 = arg2.toString().split(".")[1].length;
} catch (error) {
r2 = 0;
}
m = Math.pow(10, Math.max(r1, r2)); // 确保所有参数都为整数
return (arg1 * m + arg2 * m) / m;
}
> mathPlus(0.1, 0.2); // 0.3
> mathPlus(1, 2); // 3
减法
function mathSubtract(arg1, arg2) {
let r1, r2, m;
try {
r1 = arg1.toString().split(".")[1].length;
} catch (error) {
r1 = 0;
}
try {
r2 = arg2.toString().split(".")[1].length;
} catch (error) {
r2 = 0;
}
m = Math.pow(10, Math.max(r1, r2));
return ((arg1 * m - arg2 * m) / m);
}
> mathSubtract(0.3, 0.1); // 0.2
> mathSubtract(3, 1); // 2
乘法
function mathMultiply(arg1, arg2) {
let m = 0;
let s1 = arg1.toString();
let s2 = arg2.toString();
try {
m += s1.split('.')[1].length; // 小数相乘,小数点后个数相加
} catch (e) {}
try {
m += s2.split('.')[1].length;
} catch (e) {}
return (
(Number(s1.replace('.', '')) * Number(s2.replace('.', ''))) /
Math.pow(10, m)
);
}
> mathMultiply(0.1, 0.2); // 0.02
> mathMultiply(1, 2); // 2
除法
function mathDivide(arg1, arg2) {
let m1 = 0;
let m2 = 0;
let n1 = 0;
let n2 = 0;
try {
m1 = arg1.toString().split('.')[1].length;
} catch (e) {}
try {
m2 = arg2.toString().split('.')[1].length;
} catch (e) {}
n1 = Number(arg1.toString().replace('.', ''));
n2 = Number(arg2.toString().replace('.', ''));
/**
* 将除法转换成乘法
* 乘以它们的小数点后个数差
*/
return mathMultiply(n1 / n2, Math.pow(10, m2 - m1));
}
// > 0.2 / 0.03 => 6.666666666666667
> mathDivide(0.2, 0.03); // 6.666666666666665
> mathDivide(0.3, 0.1); // 3
> mathDivide(3, 1); // 3
引入第三方库
站在前人的肩膀上,可以前进的更快。下面这些成熟的库封装了很多实用的函数,虽然部分函数可能永远不会用到
Math.js
介绍:功能强大,内置大量函数,体积较大
GitHub - josdejong/mathjs: An extensive math library for JavaScript and Node.js
https://github.com/josdejong/mathjs
decimal.js
介绍:支持三角函数等,并支持非整数幂
GitHub - MikeMcl/decimal.js: An arbitrary-precision Decimal type for JavaScript
https://github.com/MikeMcl/decimal.js
big.js
介绍:体积6k,提供了CDN
GitHub - MikeMcl/big.js: A small, fast JavaScript library for arbitrary-precision decimal arithmetic.
https://github.com/MikeMcl/big.js
number-precision
介绍:体积很小,只有1k左右
GitHub - nefe/number-precision: 🚀1K tiny & fast lib for doing addition, subtraction, multiplication and division operations precisely
https://github.com/nefe/number-precision
0.1 + 0.2 不等于 0.3 ?这是为什么?一篇讲清楚!
在很多编程语言中,我们都会发现一个奇怪的现象,就是计算 0.1 + 0.2,它得到的结果并不是 0.3,比如 C、C++、JavaScript 、Python、Java、Ruby 等,都会有这个问题。
~

为此,有人还做出了一个 https://0.30000000000000004.com/ 网站,在这个网站上我们可以找到哪些编程语言在计算 0.1 + 0.2 的结果并不是 0.3,而是 0.30000000000000004。
我们可以用 JavaScript 来做演示,计算 0.1 + 0.2,它得到的结果并不是0.3,而是 0.30000000000000004。

当然如果你把它作为条件判断语句,返回的也是 false:

还有其他的例子:
6 * 0.1 = 0.6 但计算机显示为 0.6000000000000001
0.11 + 0.12 = 0.23 但计算机显示为 0.22999999999999998
0.1 + 0.7 = 0.8 但计算机显示为 0.7999999999999999
0.3+0.6 = 0.9 但计算机显示为0.8999999999999999
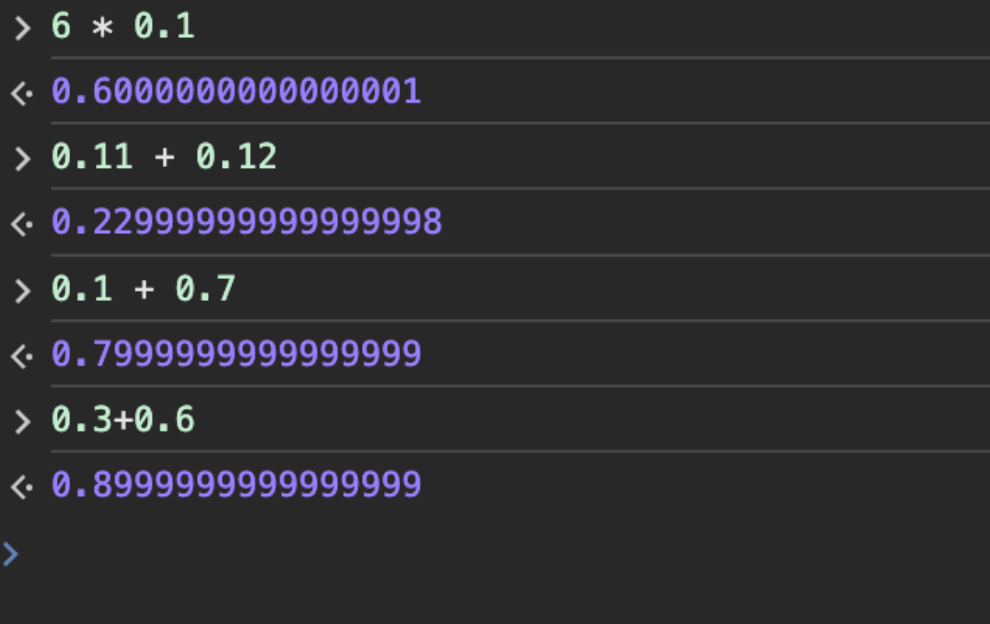
而以下几个计算式却能得到我们想要的结果:
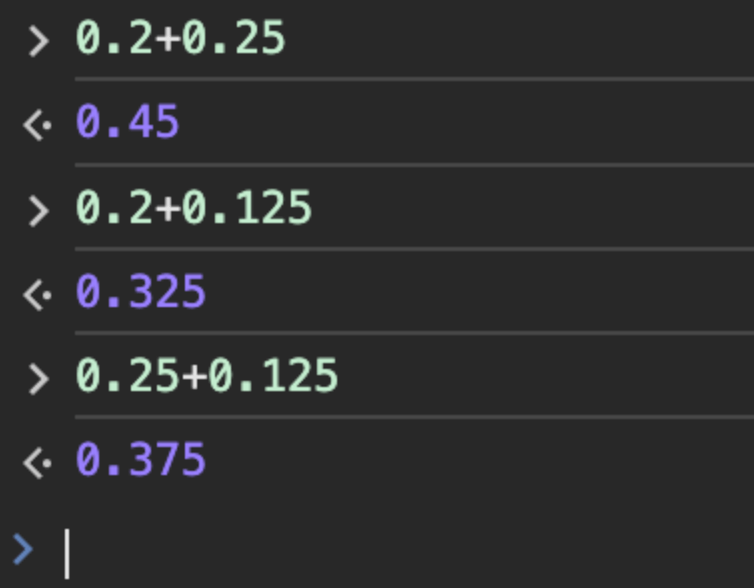
这是为什么呢?
简单来说,计算机使用基于二进制的浮点数,而我们人类使用基于十进制的浮点数。
在二进制中,,浮点数通常使用 IEEE 754 标准进行表示,无法准确表示的小数有 0.1、0.2 或 0.3 这样的数字,因为它使用的是二进制浮点格式。
IEEE 754 标准可以参见:https://zh.wikipedia.org/wiki/IEEE_754
背后原理
在十进制系统中,如果一个分数使用基数(10)的质因数来表示,那么它可以被精确地表示。
10 的质因数是 2 和 5。
因此,1/2、1/4、1/5 (0.2)、1/8 和 1/10 (0.1) 可以被精确地表示,因为分母使用了 10 的质因数。
而 1/3、1/6 和 1/7 是无限循环的小数,因为分母使用了 3 或 7 的质因数。
在二进制(计算机使用的系统)中,如果一个分数使用基数(2)的质因数来表示,那么它可以被精确地表示。
2 是 2 的唯一质因数。
因此,1/2、1/4 和 1/8 都可以被精确地表示,因为分母使用了 2 的质因数。
而 1/5 (0.2) 或 1/10 (0.1) 是无限循环的小数,因为分母使用了 5 或 10 的质因数。
所以当我们尝试表示像 0.1 这样的十进制小数时,计算机会使用一个近似值。这个近似值是通过将无限循环的二进制小数转换为有限位数的浮点数表示来实现的。
因此,当我们在计算机中进行浮点数运算时,结果可能会有微小的误差。
例如,0.1 在二进制中的近似表示可能是 0.000110011001100…,但在计算机的浮点数表示中,它可能被截断或舍入为 0.00011001100110,这就导致了 0.1 + 0.2 在计算机中可能不等于 0.3,而是略微有所偏差。
0.1 是十分之一(1/10),要得到 0.1 的二进制表示(即二进制形式),我们需要使用二进制长除法,即将二进制数1除以二进制的 1010(即1/1010),如下所示:
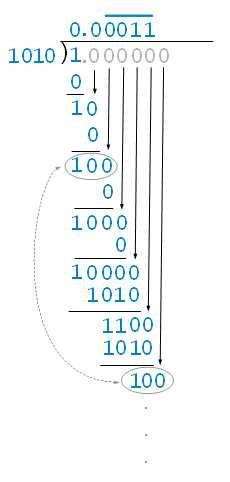
因此,0.1 在二进制中的表示为 0.0001100110011001100110011…(无限循环)。
这个无限循环的模式 0011 会一直重复下去,因为二进制系统只能通过这种方式来近似表示十进制中的 0.1。
在实际的计算机系统中,这个无限循环的小数会被截断为有限位数,以便存储和计算。这就导致了在计算机中进行二进制浮点数运算时,可能会出现精度损失,从而使得 0.1 和 0.2 的和不完全等于0.3。
十进制小数转二进制
还有一种更容易理解的方法(采用 *2 取整法),例如我们要把十进制数的小数 0.875 转换为二进制数,只需将十进制数的小数部分乘以 2,然后提取整数部分,直到小数部分变为 0。
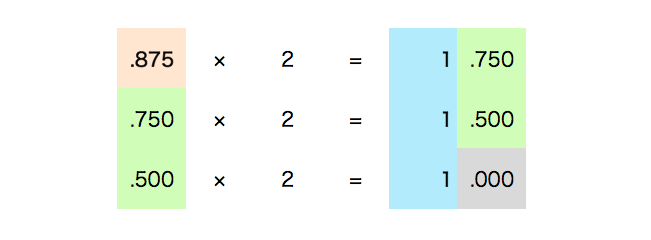
将上面提取的整数部分排列的结果 111 变成以二进制表示的 .875。
二进制数 1101.111 整数部分为 1101 ,小数部分为 111,就是十进制数 13.875 转换为二进制的结果。
按以上的方法我们将十进制小数 0.1 转化为二进制就是:
0.1 = 0.0001100110011001100110011001100110011001100110011001101...

十进制小数 0.2 转化为二进制就是:
0.2 = 0.001100110011001100110011001100110011001100110011001101...

解决办法
1、小数先转整数
可以先把小数转换成整数,再相加之后转回小数,如下实例:
(0.1*10 + 0.2*10)/10
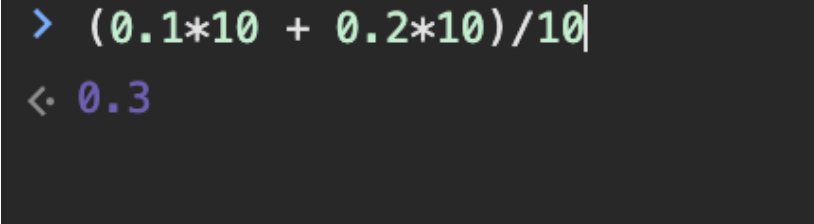
2、使用 toFixed() 方法
toFixed() 方法可以将一个数字转换为指定小数位数的字符串表示形式。
下面是一个使用 toFixed() 方法解决浮点数精度问题的例子:
let sum = 0.1 + 0.2;
console.log(sum.toFixed(2)); // 输出: 0.30
需要注意的是,toFixed()方法虽然在显示上解决了问题,但它并没有改变数字的实际值,它只是改变了数字的表示形式。
如果你需要进行精确的数学运算,可能需要使用其他方法,比如引入一个精度更高的数值类型或者使用第三方的数学库来处理浮点数运算。
3、使用 decimal.js 库
在 JavaScript 中处理浮点数的精度问题时,使用 decimal.js 库是一个更为精确和可靠的解决方案。
decimal.js 是一个任意精度的十进制数学库,它能够避免原生 JavaScript 中浮点数运算的不精确性。
Github 地址:https://github.com/MikeMcl/decimal.js
首先,你需要在你的项目中引入 decimal.js 库。
使用 npm 安装:
npm install decimal.js
在 HTML 中引入:
<script src="https://cdnjs.cloudflare.com/ajax/libs/decimal.js/10.2.0/decimal.min.js"></script>
接下来,你可以使用 decimal.js 来处理浮点数的运算,下面是一个例子:
实例
// 引入Decimal构造函数
const Decimal = decimal. Decimal;
// 创建两个Decimal对象
let a = new Decimal(‘0.1’);
let b = new Decimal(‘0.2’);
// 进行加法运算
let sum = a.plus(b);
// 输出结果
console.log(sum.toString()); // 输出: 0.3
使用 decimal.js 库得到的结果是准确的 0.3,而不是原生 JavaScript 中的近似值。
via:
-
漫话:如何给女朋友解释为什么计算机中 0.2 + 0.1 不等于 0.3 ? 原创 漫话编程 2020 年 10 月 12 日 12:00
-
一个神奇的网站 0.30000000000000004.com 原创 胡译胡说 计算机奇闻逸事 2024 年 08 月 13 日 17:03 北京
-
0.1 + 0.2 不等于 0.3 ?这是为什么?一篇讲清楚!
-
javascript - 都知道0.1+0.2 = 0.30000000000000004,那要怎么让它等于 0.3 - SegmentFault
JS魔法堂:彻底理解0.1 + 0.2 === 0.30000000000000004的背后
肥仔John
Brief
一天有个朋友问我“JS中计算0.7 * 180怎么会等于125.99999999998,坑也太多了吧!”那时我猜测是二进制表示数值时发生round-off error所导致,但并不清楚具体是如何导致,并且有什么方法去规避。于是用了3周时间静下心把这个问题搞懂,在学习的过程中还发现不仅0.7 * 180==125.99999999998,还有以下的坑
- 著名的 0.1 + 0.2 === 0.30000000000000004
- 1000000000000000128 === 1000000000000000129
IEEE 754 Floating-point
众所周知,JavaScript 仅有 Number 这个数值类型,而 Number 采用的是 IEEE 754 64 位双精度浮点数编码。浮点数表示方式具有以下特点:
- 浮点数可表示的值范围比同等位数的整数表示方式的值范围要大得多;
- 浮点数无法精确表示其值范围内的所有数值,而有符号和无符号整数则是精确表示其值范围内的每个数值;
- 浮点数只能精确表示 m × 2 e m \times 2^e m×2e 的数值;
- 当 biased-exponent 为 2 e − 1 − 1 2^{e-1} - 1 2e−1−1 时,浮点数能精确表示该范围内的各整数值;
- 当 biased-exponent 不为 2 e − 1 − 1 2^{e-1} - 1 2e−1−1 时,浮点数不能精确表示该范围内的各整数值。
由于部分数值无法精确表示(存储),于是运算统计后偏差会愈见明显。
Why 0.1 + 0.2 = = = 0.30000000000000004 0.1 + 0.2 === 0.30000000000000004 0.1+0.2===0.30000000000000004?
在浮点数运算中产生误差值的示例中,最出名的应该是 0.1 + 0.2 = = = 0.30000000000000004 0.1 + 0.2 === 0.30000000000000004 0.1+0.2===0.30000000000000004 了,到底有多有名?
看看这个网站就知道了 http://0.30000000000000004.com
也就是说,不仅是 JavaScript 会产生这种问题,只要是采用 IEEE 754 Floating-point 的浮点数编码方式来表示浮点数时,则会产生这类问题。下面我们来分析整个运算过程。
-
0.1 0.1 0.1 的二进制表示为 1.1001100110011001100110011001100110011001100110011001 … × 2 − 4 1.1001100110011001100110011001100110011001100110011001 \ldots \times 2^{-4} 1.1001100110011001100110011001100110011001100110011001…×2−4
-
当 64 位的存储空间无法存储完整的无限循环小数,而 IEEE 754 Floating-point 采用 round to nearest, tie to even 的舍入模式,因此 0.1 0.1 0.1实际存储时的位模式是
0 − 01111111011 − 100110011001100110011001100110011001100110011001010 0-01111111011-100110011001100110011001100110011001100110011001010 0−01111111011−100110011001100110011001100110011001100110011001010 -
0.2 0.2 0.2 的二进制表示为 1.1001100110011001100110011001100110011001100110011001 … × 2 − 3 1.1001100110011001100110011001100110011001100110011001 \ldots \times 2^{-3} 1.1001100110011001100110011001100110011001100110011001…×2−3
-
当 64 位的存储空间无法存储完整的无限循环小数,而 IEEE 754 Floating-point 采用 round to nearest, tie to even 的舍入模式,因此 0.2 0.2 0.2 实际存储时的位模式是
0 − 01111111100 − 100110011001100110011001100110011001100110011001010 0-01111111100-100110011001100110011001100110011001100110011001010 0−01111111100−100110011001100110011001100110011001100110011001010 -
实际存储的位模式作为操作数进行浮点数加法,得到
0 − 01111111101 − 0011001100110011001100110011001100110011001100110100 0-01111111101-0011001100110011001100110011001100110011001100110100 0−01111111101−0011001100110011001100110011001100110011001100110100
转换为十进制即为 0.30000000000000004 0.30000000000000004 0.30000000000000004
Why 0.7 * 180===125.99999999998?
-
0.7 实际存储时的位模式是
0-01111111110-0110011001100110011001100110011001100110011001100110
-
180 实际存储时的位模式是
0-10000000110-0110100000000000000000000000000000000000000000000000
-
实际存储的位模式作为操作数进行浮点数乘法,得到
0-10000000101-1111011111111111111111111111111111111111101010000001
转换为十进制即为 125.99999999998
Why 1000000000000000128 === 1000000000000000129?
-
1000000000000000128 实际存储时的位模式是0-10000111010-1011110000010110110101100111010011101100100000000001;
-
1000000000000000129 实际存储时的位模式是0-10000111010-1011110000010110110101100111010011101100100000000001;
-
因此 1000000000000000128 和1000000000000000129 的实际存储的位模式是一样的。
Solution
到这里我们都理解只要采取IEEE 754 FP的浮点数编码的语言均会出现上述问题,只是它们的标准类库已经为我们提供了解决方案而已。而JS呢?显然没有。坏处自然是掉坑了,而好处恰恰也是掉坑了:)
针对不同的应用需求,我们有不同的实现方式。
Solution 0x00 - Simple implementation
对于小数和小整数的简单运算可用如下方式
function numAdd(num1/*:String*/, num2/*:String*/) {
var baseNum, baseNum1, baseNum2;
try {
baseNum1 = num1.split(".")[1].length;
} catch (e) {
baseNum1 = 0;
}
try {
baseNum2 = num2.split(".")[1].length;
} catch (e) {
baseNum2 = 0;
}
baseNum = Math.pow(10, Math.max(baseNum1, baseNum2));
return (num1 * baseNum + num2 * baseNum) / baseNum;
};
Solution 0x01 - math.js
若需要复杂且全面的运算功能那必须上math.js,其内部引用了decimal.js和fraction.js。功能异常强大,用于生产环境上妥妥的!
Solution 0x02 - D.js
D.js算是我的练手项目吧,截止本文发表时D.js版本为V0.2.0,仅实现了加、减、乘和整除运算而已,bug是一堆堆的,但至少解决了0.1+0.2的问题了。
var sum = D.add(0.1, 0.2)
console.log(sum + '') // 0.3
var product = D.mul("1e-2", "2e-4")
console.log(product + '') // 0.000002
var quotient = D.div(-3, 2)
console.log(quotient + '') // -(1+1/2)
解题思路:
- 由于仅位于Number.MIN_SAFE_INTEGER和Number.MAX_SAFE_INTEGER间的整数才能被精准地表示,也就是只要保证运算过程的操作数和结果均落在这个阀值内,那么运算结果就是精准无误的;
- 问题的关键落在如何将小数和极大数转换或拆分为Number.MIN_SAFE_INTEGER至Number.MAX_SAFE_INTEGER阀值间的数了;
- 小数转换为整数,自然就是通过科学计数法表示,并通过右移小数点,减小幂的方式处理;(如0.000123 等价于 123 * 10-6)
- 而极大数则需要拆分,拆分的规则是多样的。
- 按因式拆分:假设对12345进行拆分得到 5 * 2469;
- 按位拆分:假设以3个数值为一组对12345进行拆分得到345和12,而实际值为12*1000 + 345。
就我而言,1 的拆分规则结构不稳定,而且不直观;而 2 的规则直观,且拆分和恢复的公式固定。
- 余数由符号位、分子和分母组成,而符号与整数部分一致,因此只需考虑如何表示分子和分母即可。
- 无限循环数则仅需考虑如何表示循环数段即可。(如10.2343434则分成10.23 和循环数34和34的权重即可)
得到编码规则后,那就剩下基于指定编码如何实现各种运算的问题了。
- 基于上述的数值编码规则如何实现加、减运算呢?
- 基于上述的数值编码规则如何实现乘、除运算呢?(其实只要加、减运算解决了,乘除必然可解,就是效率问题而已)
- 基于上述的数值编码规则如何实现其它如sin、tan、%等数学运算呢?
另外由于涉及数学运算,那么将作为add、sub、mul和div等入参的变量保持如同数学公式运算数般纯净(Persistent/Immutable Data Structure)是必须的,那是否还要引入immutable.js呢?(D.js现在采用按需生成副本的方式,可预见随着代码量的增加,这种方式会导致整体代码无法维护)
Conclusion
依照我的尿性,D.js将采取不定期持续更新的策略(待我理解Persistent/Immutable Data Structure后吧:))。欢迎各位指教!
Thanks
-
Annotated ES5
http://es5.github.io/ -
GitHub - MikeMcl/decimal.js: An arbitrary-precision Decimal type for JavaScript
https://github.com/MikeMcl/decimal.js/ -
浮点数的二进制表示 - 阮一峰的网络日志
http://www.ruanyifeng.com/blog/2010/06/ieee_floating-point_representation.html -
JavaScript 中小数和大整数的精度丢失 | Demon’s Blog
https://demon.tw/copy-paste/javascript-precision.html
想了解更多浮点数的知识可参考以下文章:
细说浮点数
肥仔John
Brief
本来只打算理解 JS 中 0.1 + 0.2 == 0.30000000000000004 的原因,但发现自己对计算机的数字表示和运算十分陌生,于是只好恶补一下。
本篇我们一起来探讨一下基础 —— 浮点数的表示方式和加减乘除运算。
在深入前有两点我们要明确的:
- 在同等位数的情况下,浮点数可表示的数值范围比整数的大;
- 浮点数无法精确表示其数值范围内的所有数值,只能精确表示可用科学计数法 m*2e 表示的数值而已;
(如 0.5 的科学计数法是 2-1,则可被精确存储;而 0.2 则无法被精确存储)
- 浮点数不仅可表示有限的实数,还可以表示有限的整数。
Encode
20 世纪 80 年代前每个计算机制造商都自定义自己的表示浮点数的规则,及浮点数执行运算的细节。而且不太关注运算的精确性,而是更多地关注速度和简便性。
1985 年左右推出 IEEE 754 标准的浮点数表示和运算规则,才让浮点数的表示和运算均有可移植性。(IEEE,读作 Eye-Triple-Eee,电器与电子工程师协会)
上述的 IEEE 754 称为 IEEE 754-1985 Floating point,直到 2008 年对其进行改进得到我们现在使用的 IEEE 754-2008 Floating point 标准。
IEEE 754 的二进制编码由 3 部分组成,分别是 sign-bit (符号位),biased-exponent (基于偏移的阶码域) 和 significant (尾数 / 有效数域)。
Sign-bit: 0 表示正,1 表示负。占 1bit;
Biased-exponent: 首先 exponent 表示该域用于表示指数,也就是数值可表示数值范围,而 biased 则表示它采用偏移的编码方式。那么什么是采用偏移的编码方式呢?也就是位模式中没有设立 sign-bit,而是通过设置一个中间值作为 0,小于该中间值则为负数,大于该中间值则为正数。IEEE 754 中规定
bias = 2 e − 1 − 1 \text{bias} = 2^{e-1} - 1 bias=2e−1−1
其中 e e e 为 Biased-exponent 所占位数。
Significant: 表示有效数,也就是数值可表示的精度。(注意:Significant 采用原码编码;假设有效数位模式为 0101,那么其值为 0 × 2 − 1 + 1 × 2 − 2 + 0 × 2 − 3 + 1 × 2 − 4 0 \times 2^{-1} + 1 \times 2^{-2} + 0 \times 2^{-3} + 1 \times 2^{-4} 0×2−1+1×2−2+0×2−3+1×2−4 即有效数域的指数为负数。)
另外 IEEE 754 还提供 4 个精度级别的浮点数定义 (单精度、双精度、延生单精度和延生双精度),单精度和双精度具体定义如下:
| Level | Width (bit) | Range at full precision | Width of biased-exponent (bit) | Width of significant (bit) |
|---|---|---|---|---|
| Single Precision | 32 | 1.1810-38 ~ 3.41038 | 8 | 23 |
| Double Precision | 64 | 2.2310-308 ~ 1.8010308 | 11 | 52 |
为了简便,下面以 Single Precision 来作叙述。

现在我们了解到 32bit 的浮点数由 3 部分组成,那么它们具体又有怎样的组合规则呢?
具体分为 4 种:
1、Normalized (规格化)
编码规则
-
biased-exponent ≠ 0 & & biased-exponent ≠ 2 e − 1 \text{biased-exponent} \neq 0 \, \&\& \, \text{biased-exponent} \neq 2^{e-1} biased-exponent=0&&biased-exponent=2e−1
∧ \land ∧ ; & & \, \&\& \, &&
-
exponent = biased-exponent − Bias \text{exponent} = \text{biased-exponent} - \text{Bias} exponent=biased-exponent−Bias,其中 exponent 是指实际的指数值;
-
significant 前默认含数值为 1 的隐藏位 (implied leading 1),即若 significant 域存储的是 0001,而实际值是 10001。
2、Denormalized (非规格化)
用于表示非常接近 0 的数值和 +0 和 -0。
+0 的位模式为: 0 - 00000000 - 00000000000000000000000 0\text{-}00000000\text{-}00000000000000000000000 0-00000000-00000000000000000000000
-0 的位模式为: 1 - 00000000 - 00000000000000000000000 1\text{-}00000000\text{-}00000000000000000000000 1-00000000-00000000000000000000000
编码规则
-
biased-exponent = = 0 \text{biased-exponent} == 0 biased-exponent==0 ;
-
exponent = 1 − Bias \text{exponent} = 1 - \text{Bias} exponent=1−Bias,其中 exponent 是指实际的指数值;
-
significant 前默认含数值为 0 的隐藏位 (implied leading 1),即若 significant 域存储的是 0001,而实际值是 00001。
3、Infinity (无限大)
用于表示溢出。
编码规则
-
biased-exponent = = 2 e − 1 \text{biased-exponent} == 2^{e-1} biased-exponent==2e−1
-
significant = = 0 \text{significant} == 0 significant==0
运算结果为 Infinity 的表达式
-
Infinity = = N 0 \text{Infinity} == \frac{N}{0} Infinity==0N,其中 N 为任意正数;
-
− Infinity = = N − 0 -\text{Infinity} == \frac{N}{-0} −Infinity==−0N,其中 N 为任意正数;
-
Infinity = = Infinity × N \text{Infinity} == \text{Infinity} \times N Infinity==Infinity×N,其中 N 为任意正数。
4、NaN (非数值)
用于表示 结果既不是 实数 又不是 无穷。
编码规则
-
biased-exponent = = 2 e − 1 \text{biased-exponent} == 2^{e-1} biased-exponent==2e−1 ;
-
significant ≠ 0 \text{significant} \neq 0 significant=0。
运算结果为 NaN 的表达式
-
Math.sqrt ( − 1 ) \text{Math.sqrt} (-1) Math.sqrt(−1)
-
Infinity − Infinity \text{Infinity} - \text{Infinity} Infinity−Infinity
-
Infinity × 0 \text{Infinity} \times 0 Infinity×0
-
0 0 \frac{0}{0} 00
注意
-
NaN 与任何数值作运算,结果均为 NaN:
-
NaN ≠ NaN \text{NaN} \neq \text{NaN} NaN=NaN
-
1 = Math.pow(NaN, 0) 1 = \text{Math.pow(NaN, 0)} 1=Math.pow(NaN, 0)
NaN 在浮点运算中的特殊性质和行为
Rounding modes (aka Rounding scheme,舍入模式)
由于浮点数无法精确表示所有数值,因此在存储前必须对数值作舍入操作。具体分为以下 5 种舍入模式
1. Round to nearest, ties to even (IEEE 754 默认的舍入模式)
舍入到最接近且可以表示的值,当存在两个数一样接近时,取偶数值。(如 2.4 舍入为 2,2.6 舍入为 3;2.5 舍入为 2,1.5 舍入为 2。)
Q:为什么会当存在两个数一样接近时,取偶数值呢?
A:由于其他舍入方式均令结果单方向偏移,导致在运算时出现较大的统计偏差。而采用这种偏移则 50% 的机会偏移两端方向,从而减少偏差。
2. Round to nearest, ties to zero
舍入到最接近且可以表示的值,当存在两个数一样接近时,取离 0 较远的数值
3. Round to infinity
向正无穷方向舍入
4. Round to negative infinity
向负无穷方向舍入
5. Round to zero
向 0 方向舍入
Overflow
到这里我们对浮点数的表示方式已经有一定程度的了解了,也许你会迫不及待想了解它的运算规则,但在这之前我想大家应该要想理解溢出和如何判断溢出,不然无法理解后续对运算的讲解。
Q1:何为溢出?
A1:溢出,就是运算结果超出可表示的数值范围。注意:进位、借位不一定会产生溢出。
发生溢出:
4 位有符号整数 7+7
0111
- 0111
1110 => -2
只有最高数值位发生进位,因此发生溢出
没有发生溢出:
4 位有符号整数 7-2
0111
- 1110
10101 => 取模后得到 5
符号位和最高数值位均发生进位,因此没有发生溢出
Q2:如何判断溢出?
A2:有两种方式判断溢出,分别是 进位判断法 和 双符号判断法。
- 进位判断法 *
前提:采用单符号位,即 + 4 的二进制位模式为 0100。
无溢出:符号位 和 数值域最高位 一起进位或一起不发生进位。
溢出:符号位 或 数值域最高位 其中一个发生进位。
- 双符号判断法 *
前提:采用双符号位,即 + 4 的二进制位模式为 00100。
无溢出:两符号位相同。
上溢出:两符号位为 01。
下溢出:两符号位为 10。
Q3:溢出在有符号整数和浮点数间的区别?
A3:对于有符号整数而言,溢出意味着运算结果将与期待值不同从而导致错误;
对于浮点数而言,会对上溢出和下溢出进行特殊处理,从而返回一个可被 IEEE 754 表示的浮点数。
因此对于有符号整数的运算我们采用进位判断法判断溢出即可,而对于浮点数则需要采用双符号判断法了。
*Q4:浮点数运算中上溢出和下溢出具体的特殊处理是什么啊?*
A4:首先浮点数运算中仅对阶码进行溢出判断,当阶码出现下溢出时运算结果为 0(符号取决于符号位);当阶码出现上溢出时运算结果为 Infinity(符号取决于符号位)。
PS:发生溢出时,当前程序会被挂起,并发送溢出中断信号量,此时溢出中断处理程序接收信号量后会做对应的处理。
Addition & Subtraction
恭喜你还没被上述的前置知识搞晕而选择 X 掉网页,下面我们终于可以着手处理运算问题,顺便验证一下自己对上述内容是否真的理解了。
步骤:
- 对 0、Infinity 和 NaN 操作数作检查
若有一个操作数为 NaN 则直接返回 NaN;
若有一个操作数为 0 则直接返回另一个操作数;
若有一个操作数为 Infinity,
若另一个操作数也是 Infinity 且符号相同则返回第一个操作数;
若另一个操作数也是 Infinity 且符号不同则返回 NaN;
若其他情况则返回 Infinity。
- 对阶,若两操作数的阶码不相等,则对阶(小数点对齐)。
由于尾数右移所损失的精度比左移的小,因此小阶向大阶看齐。
- 符号位 + 尾数(包含隐藏位)执行加减法。
按有符号整数加减法进行运算,并采用双符号法判断是否溢出。
- 规格化。
向右规格化:若步骤 3 出现溢出,则尾数右移 1 位,阶码 + 1;
向左规格化:若步骤 3 没有出现溢出,且数值域最高位与符号位数值相同,则尾数左移 1 位且阶码 - 1,直到数值域最高位为 1 为止。
-
舍入处理
-
溢出判断
由于规格化时可能会导致阶码发生溢出
若无发生溢出,则运算正常结束。
若发生上溢出,则返回 Infinity。
若发生下溢出,则返回 0。
示例 1,0.75+(-0.75) = 0:
0.75+(-0.75) = 0
以 8 位存储,尾数采用原码编码
0.75 存储位模式 0-0110-100
-0.75 存储位模式 1-0110-100
-
对阶
阶码一样跳过。 -
符号位 + 尾数(含隐藏位)相加
由于尾数以有符号数的方式进行运算,因此要对尾数进行取补操作
00-1100
+11-0100
100-0000
对符号位截断后得到 00-0000 -
规格化
根据符号位相同,则执行左规格化操作,也就是尾数不断向左移而阶码不断减 1,直到尾数最高位为 1 为止。 -
舍入处理
000 -
溢出判断
在执行规格化时发生阶码下溢出,整体结果返回 0-0000-000.
示例 2,0.75-0.25 = 0.5:
0.75-0.25 = 0.5
以 8 位存储,尾数采用原码编码
0.75 存储位模式 0-0110-100
0.25 存储位模式 0-0101-000
-
对阶
0.25 的阶码小于 0.75 相同,因此 0.25 向 0.75 的看齐。
0-0110-100 -
尾数相加 (采用双位符号法),减法转换为加法,对 0.75 和 - 0.25 取补
00-1100
+11-1100
100-1000
对符号位截断后得到 00-1000 -
规格化
根据符号位相同,则执行左规格化操作,也就是尾数不断向左移而阶码不断减 1,直到尾数最高位为 1 为止。 -
舍入处理
1000 -
溢出判断
阶码没有发生溢出,正常返回运算结果 0-0110-000 (注意:舍入处理后数值域的最高位是位于隐藏位的)
示例 3, 0.25-0.75 = -0.5:
Comparison
比较运算 (cmp 指令) 实际上就是对两操作数做减法,然后通过标志寄存器(80x86 的 rflags)中的 CF (Carry flag)、ZF (Zero flag)、OF (Overflow flag)、SF (Sign flag) 状态标志来判断两者的关系。
对于无符号数 A 与 B 而言,则是通过 CF 和 ZF 来判断。
- 若 CF 为 1,表示 A-B 时 A 发生借位操作,那么可以判定 A<B
- 若 CF 为 0 且 ZF 不为 0,表示 A-B 时没有发生借位操作,那么可以判定 A>B
- 若 ZF 为 0,则可判定 A==B
对于有符号数 C 和 D 而言,则是通过 ZF、OF 和 SF 来判断。
- 若 ZF 为 1,则可判定 C == D
- 若 SF 为 0,OF 为 0,表示结果为正数且没有发生溢出,则 C>D
- 若 SF 为 0,OF 为 1,表示结果为正数且发生溢出,则 C<D
- 若 SF 为 1,OF 为 0,表示结果为负数且没有发生溢出,则 C<D
- 若 SF 为 1,OF 为 1,表示结果为负数且发生溢出,则 C>D
而对于浮点数而言,由于阶码域采用的是 biased-exponent 的编码方式,因此在进行比较时我们可以将整个浮点数看作有符号数来执行减法运算即可,而不必执行 Addition/Subtraction 那样繁琐的运算步骤。
Multiplication
步骤:
- 对 0、Infinity 和 NaN 操作数作检查
若有一个操作数为 NaN 则直接返回 NaN;
若有一个操作数为 0 则直接返回另一个操作数;
若有一个操作数为 Infinity,
若另一个操作数也是 Infinity 且符号相同则返回第一个操作数;
若另一个操作数也是 Infinity 且符号不同则返回 NaN;
若其他情况则返回 Infinity。
- 计算阶码(公式:e = e1 + e2 - Bias)
公式推导过程:
∵ E1 = e1 - Bias
∵ E2 = e2 - Bias
∴ E = E1+E2 = e1 + e2 - 2*Bias
∵ e = E + Bias
∴ e = e1 + e2 - Bias
对非规格化 e1 为 1
注意:计算阶码时,是执行无符号数的加减法。
- 尾数相乘
注意:尾数相乘时,是执行无符号数的乘法,并且不对结果进行截断。
-
结果左规格化,尾数左移,且阶码减 1,直到最高位为 1 为止
-
舍入处理
-
溢出判断
由于规格化时可能会导致阶码发生溢出
若无发生溢出,则运算正常结束。
若发生上溢出,则返回 Infinity。
若发生下溢出,则返回 0。
- 符号位执行 异或 运算
示例,0.5*(-0.25) = -0.125:
0.5*(-0.25) = -0.125
以 8 位存储,尾数采用原码编码
0.5 存储位模式 0-0110-000
-0.25 存储位模式 1-0101-000
-
计算阶码 (公式 e1+e2-Bias)
0110
+0101
1011
+1001
10100 取模得到 0100 -
尾数相乘
1000*1000
1000<<(3+1) - 1000<<(3)
1000000
- 0100000
减法转换为加法
1000000
+1100000
10100000 取模得到 0100000
-
左规格化
0100000 左移 1 位得到 100000
阶码 - 1 得到 0011 -
舍入处理
尾数为 1000 -
溢出判断
无溢出 -
符号位异
0 xor 1 = 1
结果
1-0011-000
Divsion
步骤:
-
对 0、Infinity 和 NaN 操作数作检查
- 若有一个操作数为 NaN,则直接返回 NaN。
- 若有一个操作数为 0,则直接返回另一个操作数。
- 若有一个操作数为 Infinity:
- 若另一个操作数也是 Infinity 且符号相同,则返回第一个操作数。
- 若另一个操作数也是 Infinity 且符号不同,则返回 NaN。
- 若其他情况则返回 Infinity。
这个逻辑确保了在进行浮点数运算时能正确处理特殊值,从而避免不确定性或不合法的计算结果。
- 计算阶码(公式: e = e 1 − e 2 + Bias + ( m − 1 ) e = e_1 - e_2 + \text{Bias} + (m - 1) e=e1−e2+Bias+(m−1))
公式推导过程:
∵ E 1 = e 1 − Bias ∵ E_1 = e_1 - \text{Bias} ∵E1=e1−Bias
∴ E 2 = e 2 − Bias ∴ E_2 = e_2 - \text{Bias} ∴E2=e2−Bias
∴ E = E 1 − E 2 = e 1 − e 2 ∴ E = E_1 - E_2 = e_1 - e_2 ∴E=E1−E2=e1−e2
∵ e = E + Bias ∵ e = E + \text{Bias} ∵e=E+Bias
∴ e = e 1 − e 2 + Bias ∴ e = e_1 - e_2 + \text{Bias} ∴e=e1−e2+Bias
∵ 除法会消权,因此通过移位去除负指数以便后续计算 ∵ \text{除法会消权,因此通过移位去除负指数以便后续计算} ∵除法会消权,因此通过移位去除负指数以便后续计算
∴ e = e 1 − e 2 + Bias + ( m − 1 ) ,其中 m 为尾数的位数 ∴ e = e_1 - e_2 + \text{Bias} + (m - 1),其中 m 为尾数的位数 ∴e=e1−e2+Bias+(m−1),其中m为尾数的位数
对非规格化的 e 1 、 e 2 设为 1 对非规格化的 e_1、e_2 设为 1 对非规格化的e1、e2设为1
注意:计算阶码时,是执行无符号数的加减法。
- 尾数相除
注意:尾数相除时,是执行无符号数的除法,并且不对结果进行截断。
-
结果左规格化,尾数左移,且阶码减 1,直到最高位为 1 为止
-
舍入处理
-
溢出判断
由于规格化时可能会导致阶码发生溢出
若无发生溢出,则运算正常结束。
若发生上溢出,则返回 Infinity。
若发生下溢出,则返回 0。
- 符号位执行 异或 运算
示例,0.5/(-0.25) = -2:
0.5/(-0.25) = -2
以 8 位存储,尾数采用原码编码
0.5 存储位模式 0-0110-000
-0.25 存储位模式 1-0101-000
-
计算阶码 (公式 e1-e2+Bias+(m-1))
0110
+1011
10001
+00111
11000
+00011
11011
取模得到 1011 -
尾数相除
1000/1000 = 1000 >> 3 得到 0001 -
左规格化
0001 左移 3 位得到 1000
阶码 - 3 得到 1000 -
舍入处理
尾数为 1000 -
溢出判断
无溢出 -
符号位异
0 xor 1 = 1
结果
1-1000-000
Conclusion
总算写完了:) 本文以单精度作为叙述对象,为简化手工运算各示例均以 8bit 浮点数作为讲解,其实 32bit 和 64bit 的浮点数表示和运算规则与其相同,理解规则就 OK 了。
看完这么多原理性的东西,是时候总结一下我们对浮点数应有的印象了:
- 浮点数可表示的值范围比同等位数的整数表示方式的值范围要大得多;
- 浮点数无法精确表示其值范围内的所有数值,而有符号和无符号整数则是精确表示其值范围内的每个数值;
- 浮点数只能精确表示 m*2e 的数值;
- 当 biased-exponent 为 2e-1-1 时,浮点数能精确表示该范围内的各整数值;
- 当 biased-exponent 不为 2e-1-1 时,浮点数不能精确表示该范围内的各整数值。
例如:1000000000000000128 与 1000000000000000129 以双精度浮点数表示时,均为
0-10000111010-11011110000010110110101100111010011101100100000000001
若以 64bit 无符号整数表示时,1000000000000000128 为 0000110111100000101101101011001110100111011001000000000010000000;
1000000000000000129 为 0000110111100000101101101011001110100111011001000000000010000001
例子源自:Annotated ES5 http://es5.github.io/#x15.7.4.5
细说有符号整数
肥仔John
Brief
本来只打算理解 JS 中 0.1 + 0.2 == 0.30000000000000004 的原因,但发现自己对计算机的数字表示和运算十分陌生,于是只好恶补一下。
本篇我们一起来探讨一下基础 —— 有符号整数的表示方式和加减乘除运算。
Encode
有符号整数可表示正整数、0 和负整数值。其二进制编码方式包含 符号位 和 真值域。
我们以 8bit 的存储空间为例,最左 1bit 为符号位,而其余 7bit 为真值域,因此可表示的数值范围是 {-128,…,127},对应的二进制补码编码是 {10000000,…,01111111}。
从集合论的角度描述,我们可以将十进制表示的数值范围定义为集合 A,将二进制表示的数值范围定义为集合 B,他们之间的映射为 f。f (a)=b,其中 a 属于 A、b 属于 B。并且 f 为双射函数。因此有符号整数表示方式具有如下特点:
- 可表示的数值范围小;
- 十进制表示的数值范围与二进制表示的数值范围的元素是一一对应的,两者可精确映射转换。(相对浮点数而言,某些二进制表示的数值只能映射为十进制表示的数值的近似值而已);
- C 语言中虽然没有规定必须采用补码来对有符号数进行编码,但大部分实现均是采用补码。而 Java 和 C# 则明确规定采用补码来表示有符号数。
Sign-extended
符号扩展运算用于在保持数值不变、符号位不变的前提下,不同字长的整数之间的转换。
例如现在我们要将 8bit 的 10000100 扩展为 16bit,那么我们只要将高 8bit 设置为与原来符号位相同的值(这里是 1)即得到 1111111110000100,而其数值和符号并不产生变化。
Truncation
截断会减少位数,并对原始值取模。模为 2^n,n 为截断后的位数。
例如现在将 16bit 的 100000100000000100 截断为 8bit,那么结果为 00000100,而模是 2^8。
Addition
注意:位级运算均是模数运算,即加减乘除后均会对运算结果取模,并以取模后的结果作为终止返回。
有符号整数加法的运算顺序:
- 算术加法(由于采用补码对有符号数进行编码,则是已经将负数转换为正数存储,所以含负数的加法只需要直接执行算术加法即可);
- 执行截断操作。
示例 1,两个 4bit 的有符号数相加 (3+6):
0011
+0110
1001,然后执行截断得到 1001,发生正溢出得到 -7
示例 2, 两个 4bit 的有符号数相加 (-3+6):
1101
+0110
10011
然后执行截断得到 0011,发生正溢出得到 3
Subtraction
有符号整数减法的运算顺序:
- 将减法转换为加法(对减数取补码);
- 算术加法;
- 执行截断操作。
示例 1,两个 4bit 的有符号数相减 (-5-6):
1011
-0110
对减数求补码后,减法转换为加法
1011
+1010
10101,然后执行截断得到 0101,发生负溢出得到 5
示例 2,两个 4bit 的有符号数相减 (-5-(-6)):
1011
-1010
对减数求补码后,减法转换为加法
1011
+0110
10001,然后执行截断得到 0001,得到 1
Multiplication
对于乘法实质上就是通过移位操作和加、减法组合而成。
- 将乘数以二进制形式表示,并以连续的 1 作为分组。如 - 5 的二进制形式为 (1) 0 (11),从左至右可分成 2 组分别是 (1)、(11)。
- 以 n 表示每组的最高位的指数,以 m 表示每组最低位的指数。如第一组 n=m=3,第二组 n=1 而 m=0。
- 根据公式 (x<<n+1)-(x<<m) 对每组进行运算,并将结果相加。如 (假设被乘数为 - 1)
第一组:(1111)<<(3+1) - (1111)<<3 = 0000 - 1000 = 0000 + 1000 = 1000
第二组:(1111)<<(1+1) - (1111)<<0 = 1100 - 1111 = 1100 + 0001 = 1101
两组相加:1000 + 1101 = 10101,截断得到 0101,等于十进制数值 5.
2.4. 对结果取模。
Division
对于除法实质上就是通过移位操作和加、减法组合而成,且根据除数是否为 2 的 n 次幂 (n 为正数) 区别处理。
- 对于被除数为 2 的 n 次幂 (n 为正数) 的情况,除法公式为:a>>n,如 - 6/4 等价于 6/(2^2),则可转换为移位操作 - 6>>2 即可。然后再对结果取模。
- 对于被除数不为 2 的 n 次幂 (n 为正数) 的情况,则情况复杂不少。运算步骤如下:(实质上我们就是按这个步骤做十进制除法的)
2.1. 对负数取补,提取符号乘积。
2.2. 高位对齐,在除数值小于被除数值的前提下,让除数的位数等于被除数;若执行高位对齐后,除数值大于被除数时,则除数右移一位。得到位移数。
2.3. 试商,除数 - 被除数 * N = 余数中间值 ,其中 N * 被除数 <= 除数 && (N+1)* 被除数 > 除数。商 = 商 + N * 基数 ^ 位移数。
2.4. 循环执行上述步骤,直到无需再执行高位对齐,那么 2.2 中得到的余数中间值将作为除法运算的最终余数,否则余数中间值则作为一下轮高位对齐的被除数处理。
2.5. 符号乘积乘以商得到最终商,符号乘积乘以余数得到最终余数。
C 语言实现:
#include <stdio.h>
// 前置条件
const char lowest_bit_weight = 1; // 二进制最低位的位权重
int main(){
// 输入
char dividend = -5, divisor = -2;
// 输出
char quotients = 0, // 商
rem = 0; // 余数
// 中间值
char highest_bit_weight,
divisor_aligned,
tmp_dividend = dividend,
tmp_divisor = divisor;
char high_alignment;
char sign,
sign1 = 1,
sign2 = 1;
// 负数转换为正数, 求符号乘积
if (tmp_dividend < 0){
tmp_dividend = ~tmp_dividend;
tmp_dividend += 1;
sign1 = ~sign1;
sign1 += 1;
}
if (tmp_divisor < 0){
tmp_divisor = ~tmp_divisor;
tmp_divisor += 1;
sign2 = ~sign2;
sign2 += 1;
}
sign = sign1 * sign2;
// 开始运算
while (1){
// 高位对齐 (从高位开始运算)
// 结果:1. 要么被除数的最高位小于除数的最高位;
// 2. 要么被除数的最高位对齐除数的最高位, 且被除数大于除数;
high_alignment = 0;
highest_bit_weight = lowest_bit_weight;
divisor_aligned = tmp_divisor;
while (tmp_dividend >= divisor_aligned){
divisor_aligned = divisor_aligned << 1;
highest_bit_weight = highest_bit_weight << 1;
high_alignment += 1;
}
if (high_alignment > 0){
divisor_aligned = divisor_aligned >> 1;
highest_bit_weight = highest_bit_weight >> 1;
high_alignment -= 1;
}
// 当无需执行高位对齐时,则将下一轮的被除数作为余数,并且结束运算
if (0 == high_alignment) {
rem = tmp_dividend;
break;
}
// 上一轮运算的商加上最高位权重得到当前运算的商值
quotients = quotients | highest_bit_weight;
// 被除数减除数的差值作下一轮的被除数
tmp_dividend = tmp_dividend - divisor_aligned;
}
// 商*符号乘积 = 最终商,余数*符号乘积 = 最终余数
printf("%d/%d=%d(rem:%d)\n", dividend, divisor, quotients * sign, rem * sign);
return 0;
}
Convert Unsigned 2 Signed, and Convert Signed 2 Unsigned
无符号数与有符号数间转换采取的是位级表示 (位模式) 不变,解析方式变化引起最终所表示的值变化。
例如:无符号数 15 的 4bit 位模式为 1111,强制转换为有符号数时其位模式依然是 1111,但实际表示的值则变为 - 1。
无符号数转换为有符号数的公式 U2Tw (x) = x - xw-1*2w,其中 w 表示位数,x 表示无符号数的十进制值,x 表示无符号数的二进制位模式。
有符号数转换为无符号数的公式 T2Uw (x) = x + xw-1*2w,其中 w 表示位数,x 表示无符号数的十进制值,x 表示无符号数的二进制位模式。
注意:在 C 语言中若参与运算的两运算数分别是有符号数和无符号数,那么会隐式将有符号数转换为无符号数后再进行运算。
细说无符号整数
肥仔John
Brief
本来只打算理解 JS 中 0.1 + 0.2 == 0.30000000000000004 的原因,但发现自己对计算机的数字表示和运算十分陌生,于是只好恶补一下。
本篇我们一起来探讨一下基础的基础 —— 无符号整数的表示方式和加减乘除运算。
Encode
无符号整数只能表示大于或等于零的整数值。其二进制编码方式十分直观,仅包含真值域。
我们以 8bit 的存储空间为例,真值域则占 8bit,因此可表示的数值范围是 {0,…,255},对应的二进制编码是 {00000000,…,11111111}。
从集合论的角度描述,我们可以将十进制表示的数值范围定义为集合 A,将二进制表示的数值范围定义为集合 B,他们之间的映射为 f。f (a)=b,其中 a 属于 A、b 属于 B。并且 f 为双射函数。因此无符号整数表示方式具有如下特点:
- 可表示的数值范围小;
- 十进制表示的数值范围与二进制表示的数值范围的元素是一一对应的,两者可精确映射转换。(相对浮点数而言,某些二进制表示的数值只能映射为十进制表示的数值的近似值而已)
Zero-extend
零扩展运算用于在保持数值不变的前提下,不同字长的整数之间的转换。
例如现在我们要将 8bit 的 00000100 扩展为 16bit,那么我们只要将高 8bit 设置为 0 即得到 000000000000000100,而其数值并不产生变化。
Truncation
截断会减少位数,并对原始值取模。模为 2^n,n 为截断后的位数。
例如现在将 16bit 的 000000100000000100 截断为 8bit,那么结果为 00000100,而模是 2^8。
Addition
注意:位级运算均是模数运算,即加减乘除后均会对运算结果取模,并以取模后的结果作为终止返回。
无符号整数加法的运算顺序:
- 算术加法;
- 执行截断操作。
示例,两个 4bit 的无符号数相加 (11+6):
1011
+0110
10001,然后执行截断得到 0001
Subtraction
无符号整数减法的运算顺序:
- 将减法转换为加法(对减数取补码);
- 算术加法;
- 执行截断操作。
示例,两个 4bit 的无符号数相减 (11-6):
1011
-0110
对减数求补码后,减法转换为加法
1011
+1010
10101,然后执行截断得到 0101
Multiplication
对于乘法实质上就是通过移位操作和加、减法组合而成,且根据乘数是否为 2 的 n 次幂区别处理。
-
对于乘数为 2 的 n 次幂的情况,乘法公式为:
a < < n a << n a<<n
如 6 × 4 6 \times 4 6×4 等价于 6 × ( 2 2 ) 6 \times (2^2) 6×(22),则可转换为移位操作:
6 < < 2 6 << 2 6<<2
即可。然后再对结果取模。
-
对于乘数不为 2 的 n 次幂的情况:
2.1. 将乘数以二进制形式表示,并以连续的 1 作为分组。如 43 的二进制形式为 00 ( 1 ) 0 ( 1 ) 0 ( 11 ) 00(1)0(1)0(11) 00(1)0(1)0(11),从左至右可分成 3 组分别是 ( 1 ) (1) (1)、 ( 1 ) (1) (1) 和 ( 11 ) (11) (11)。
2.2. 以 n n n 表示每组的最高位的指数,以 m m m 表示每组最低位的指数。如第一组 n = m = 5 n = m = 5 n=m=5,第二组 n = m = 3 n = m = 3 n=m=3,第三组 n = 1 n = 1 n=1 而 m = 0 m = 0 m=0。
2.3. 根据公式
( x < < ( n + 1 ) ) − ( x < < m ) (x << (n + 1)) - (x << m) (x<<(n+1))−(x<<m)
对每组进行运算,并将结果相加。如(假设被乘数为 2):
-
第一组:
2 < < ( 5 + 1 ) − 2 < < 5 = 64 2 << (5 + 1) - 2 << 5 = 64 2<<(5+1)−2<<5=64 -
第二组:
2 < < ( 3 + 1 ) − 2 < < 3 = 16 2 << (3 + 1) - 2 << 3 = 16 2<<(3+1)−2<<3=16 -
第三组:
2 < < ( 1 + 1 ) − 2 < < 0 = 6 2 << (1 + 1) - 2 << 0 = 6 2<<(1+1)−2<<0=6
相加得到 86
?3
2.4. 对结果取模。
Dividision
对于除法实质上就是通过移位操作和加、减法组合而成,且根据除数是否为 2 的 n 次幂区别处理。
- 对于被除数为 2 的 n 次幂的情况,除法公式为:a>>n,如 6/4 等价于 6/(2^2),则可转换为移位操作 6>>2 即可。然后再对结果取模。
- 对于被除数不为 2 的 n 次幂的情况,则情况复杂不少。运算步骤如下:(实质上我们就是按这个步骤做十进制除法的)
2.1. 高位对齐,在除数值小于被除数值的前提下,让除数的位数等于被除数;若执行高位对齐后,除数值大于被除数时,则除数右移一位。得到位移数。
2.2. 试商,除数 - 被除数 * N = 余数中间值 ,其中 N * 被除数 <= 除数 && (N+1)* 被除数 > 除数。商 = 商 + N * 基数 ^ 位移数。
2.3. 循环执行上述步骤,直到无需再执行高位对齐,那么 2.2 中得到的余数中间值将作为除法运算的最终余数,否则余数中间值则作为一下轮高位对齐的被除数处理。
以下是 C 的实现:
#include <stdio.h>
// 前置条件
const unsigned short lowest_bit_weight = 1; // 二进制最低位的位权重
int main(){
// 输入
unsigned short dividend = 14, divisor = 5;
// 输出
unsigned short quotients = 0, // 商
rem = 0; // 余数
// 中间值
unsigned short highest_bit_weight,
divisor_aligned,
tmp_dividend = dividend;
unsigned short high_alignment;
// 开始运算
while (1){
// 高位对齐 (从高位开始运算)
// 结果:1. 要么被除数的最高位小于除数的最高位;
// 2. 要么被除数的最高位对齐除数的最高位, 且被除数大于除数;
high_alignment = 0;
highest_bit_weight = lowest_bit_weight;
divisor_aligned = divisor;
while (tmp_dividend >= divisor_aligned){
divisor_aligned = divisor_aligned << 1;
highest_bit_weight = highest_bit_weight << 1;
high_alignment += 1;
}
if (high_alignment > 0){
divisor_aligned = divisor_aligned >> 1;
highest_bit_weight = highest_bit_weight >> 1;
high_alignment -= 1;
}
// 当无需执行高位对齐时,则将下一轮的被除数作为余数,并且结束运算
if (0 == high_alignment) {
rem = tmp_dividend;
break;
}
// 上一轮运算的商加上最高位权重得到当前运算的商值
quotients = quotients | highest_bit_weight;
// 被除数减除数的差值作下一轮的被除数
tmp_dividend = tmp_dividend - divisor_aligned;
}
printf("%u/%u=%u(rem:%u)\n", dividend, divisor, quotients, rem);
return 0;
}
细说原码、反码和补码
肥仔John
Brief
在深入之前,我们先明确以下几点:
- 本篇内容全部针对有符号数整数;
- 对于有符号数整数,其在计算机中的存储结构是 符号位 + 真值域。其中符号位为 0 表示正数,1 表示负数;
- Q:既然已经有原码,那么为什么还要出现反码、补码等数值的编码方式呢?
A:由于为了降低当时计算机物理电路的设计难度,决定采用加法代替减法运算(因此计算机内部是没有减法运算的),即 10-5 被替换为 10+(-5),而反码、补码就用于解决 10+(-5) 的问题的。
True Form
原码 (称为 true form、sign-magnitude 或 sign and magnitude),就是直接将十进制数转换为二进制数形式。如 7 的原码为 0111,-6 的原码为 1110。
注意:
- 原码是区分 + 0 和 - 0 的,+0 的原码为 0000;-0 的原码为 1000;
- 若存储空间为 n bit,则原码的取值范围是 -2n-1 ~ 2n-1。
原码在以加法代替减法的运算中引起的问题:
例如在计算 0 = 1-1 = 1+(-1) = 0001 + 1001 = 1010 = -2, 发现通过原码来运算时居然会得到 0 == -2 的结果。于是引入了反码。
一般用于 IEEE 754 浮点数标准中尾数 (significant) 的表示。
Ones’ Complement
原码转换成反码的规则如下:
-
正整数原码的反码是其自身。如原码 0001 的反码是 0001;
-
负整数原码的反码则是对原码真值域的个位数取反即可。如原码 1010 的反码是 1101。
那么将反码转换为原码的规则如下:
-
正整数反码的反码是其自身。如反码 0001 的原码是 0001;
-
负整数反码的原码则是对反码真值域的个位数取反即可。如反码 1101 的原码是 1010。
注意:
- 反码是区分 + 0 和 - 0 的,+0 的反码为 0111;-0 的反码为 1111;
- 若存储空间为 n bit,则反码的取值范围是 -2n-1 ~ 2n-1。
反码在以加法代替减法的运算中引起的问题:
例如在计算 0 = 1-1 = 1+(-1) = 0001【原码】 + 1001【原码】 = 0001【反码】 + 1110【反码】= 1111【反码】 = 1000【原码】 = -0, 发现通过反码来运算时居然会得到 0 == -0 的结果。
看到采用反码运算的结果已经非常接近正确结果,但 - 0 对于我们来说还是没有太多的意义。于是引入了补码。
Two’s Complement
原码转换成补码的规则如下:
-
正整数原码的补码是其自身。如原码 0001 的补码是 0001;
-
负整数原码的补码则是对原码真值域的个位数取反后,整体 + 1 即可。如原码 1010 的补码是 1110。
那么将补码转换为原码的规则如下:
- 对补码再求一次补码则得到原码。
取补码的流程发生在符号变化时,也就是正、负数间转换。如 -(1),-(-1) 等。
具体流程如下:
- 符号位取反;
- 真值域取反;
- 整体 + 1。
因此在进行 -(1) 运算时,步骤如下(1 的补码是 0001):
- 符号位取反 ——1001
- 真值域取反 ——1110
- 整体 + 1——1111
或将步骤 1 和 2 合并为对各位取反 ——1110,然后整体 + 1——1111
在进行 -(-1) 运算时,步骤如下(-1 的补码是 1111):
- 符号位取反 ——0111
- 真值域取反 ——1000
- 整体 + 1——1001
或将步骤 1 和 2 合并为对各位取反 ——1000,然后整体 + 1——1001
注意:
- 补码是不区分 + 0 和 - 0 的,+0 和 - 0 的补码为 0000;
- 若存储空间为 n bit,则反码的取值范围是 -2n ~ 2n-1。
- 原码 + 其补码 = 0。
补码在以加法代替减法的运算的结果:
例如在计算 0 = 1-1 = 1+(-1) = 0001【原码】 + 1001【原码】 = 0001【反码】 + 1110【反码】= 0001【补码】+ 1111【补码】 = 0000【补码】 = 0000【原码】=0, 发现通过补码来运算时结果恰恰正确。
真相:有符号整数其实是以补码的编码方式存储的。因此 C 语言的 int 类型在 32 位 OS 上的值范围是:-2n ~ 2n-1。我们可以通过以下的 C 代码片段要验证:
#include <stdout.h>
#include <string.h>
int main(){
int f = -1;
unsigned long l;
int i;
char s[32];
memcpy(&l, &f, 4);
for (i = 31; i >=0; --i){
if (l % 2 == 1){
s[i] = '1';
}
else{
s[i] = '0';
}
l /= 2;
}
s[32] = '\0';
printf("%s\n", s);
return 0;
}
标准输出为:11111111111111111111111111111111(若为原码则应该是 10000000000000000000000000001)
到这里我们对原码、反码和补码有一定程度的了解,并通过死记硬背的传统学习方法答对考题应该就不成问题了。但若要自圆其说则不可避免地需要解答以下问题:
- 为什么补码的方式能解决以加法替代减法时所产生的问题?
下面我们一起来探讨和推导一下吧。
Theory
Modulus
模,是指一个计量系统的计数范围,而模则是产生“溢出”的量。
以时钟为例,时钟的计数范围是 0 到 11,而模(产生“溢出”的量)是 12。现在我们将时针从 4 点逆时针移动 2 格,和顺时针移动 10 格,得到的结果均是一样的。以算术公式表示则是 4 − 2 4 - 2 4−2 和 4 + 10 4 + 10 4+10,一眼看出 4 − 2 4 - 2 4−2 明显不等于 4 + 10 4 + 10 4+10,那为什么时钟上的两者结果却是相同的呢?
那是“模”在作怪。当运算结果超出计数范围时,则会执行求模运算, 4 + 10 = 14 > 12 4 + 10 = 14 > 12 4+10=14>12,因此 14 m o d 12 = 2 14 \mod 12 = 2 14mod12=2。这时你会发现负数的补数必定是正数,这样就解决了需要以正数表示负数的需求。接下来就要验证以补数解决以正数表示负数后,参与加法运算是否有问题了。
在深入之前,请大家先了解一下理论:
补数 / 补码 / 二补码,若 A , B A, B A,B 除以 M M M 为模执行求模运算后的结果相等,则 A A A 与 B B B 互为补数,公式可以表示为:
a ≡ b ( mod m ) a \equiv b \ (\text{mod} \ m) a≡b (mod m)
求模公式:
m o d = a − m ∗ L a / m J mod = a - m * La/mJ mod=a−m∗La/mJ
TeX 表达式:
m o d = a − m × ⌊ a m ⌋ \ mod = a - m \times \left\lfloor \frac{a}{m} \right\rfloor mod=a−m×⌊ma⌋
其中
⌊
x
⌋
\left\lfloor x \right\rfloor
⌊x⌋ 代表“取下界”符号( \left\lfloor 和 \right\rfloor 用于表示向下取整的符号,用于包围 \frac{a}{m} 表达式。注意:% 是取余而不是取模数的运算符,而求模和取余在本质上是不同的。)
通过以上理论,可以理解为何模运算能够处理减法与加法,并且在计算机中使用补数来表示负数是合理的。
以下以 JS 来描述
/**
* @description 求模
* @method mod
* @public
* @param {Number} o - 操作数
* @param {Number} m - 模,取值范围:除零外的数字(整数、小数、正数和负数)
* @returns {Number} - 取模结果的符号与模的符号保持一致
*/
var mod = (o/*perand*/, m/*odulus*/) => {
if (0 == m) throw TypeError('argument modulus must not be zero!')
return o - m * Math.floor(o/m)
}
/**
* @description 求余
* @method rem
* @public
* @param {Number} dividend - 除数
* @param {Number} divisor - 被除数,取值范围:除零外的数字(整数、小数、正数和负数)
* @returns {Number} remainder - 余数,符号与除数的符号保持一致
*/
var rem = (dividend, divisor) => {
if (0 == divisor) throw TypeError('argument divisor must not be zero!')
return dividend - divisor * Math.trunc(dividend/divisor)
}
补数定理:
1.反身性: a ≡ a ( m o d m ) a \equiv a \pmod{m} a≡a(modm)
2.对称性:若 a ≡ b ( m o d m ) a \equiv b \pmod{m} a≡b(modm),则 b ≡ a ( m o d m ) b \equiv a \pmod{m} b≡a(modm)
3.传递性:若 a ≡ b ( m o d m ) a \equiv b \pmod{m} a≡b(modm), b ≡ c ( m o d m ) b \equiv c \pmod{m} b≡c(modm),则 a ≡ c ( m o d m ) a \equiv c \pmod{m} a≡c(modm)
4.补数式相加:若 a ≡ b ( m o d m ) a \equiv b \pmod{m} a≡b(modm), c ≡ d ( m o d m ) c \equiv d \pmod{m} c≡d(modm),则 a + c ≡ b + d ( m o d m ) a+c \equiv b+d \pmod{m} a+c≡b+d(modm), a − c ≡ b − d ( m o d m ) a-c \equiv b-d \pmod{m} a−c≡b−d(modm)
5.补数式相乘:若 a ≡ b ( m o d m ) a \equiv b \pmod{m} a≡b(modm), c ≡ d ( m o d m ) c \equiv d \pmod{m} c≡d(modm),则 a c ≡ b d ( m o d m ) ac \equiv bd \pmod{m} ac≡bd(modm)
6.互为补数的绝对值相加等于模数:若 a ≡ b ( m o d m ) a \equiv b \pmod{m} a≡b(modm),则 m = ∣ a ∣ + ∣ b ∣ m = |a| + |b| m=∣a∣+∣b∣
示例 1:
对于有符号数 − 3 -3 −3(采用补码编码:1101),模 m m m 为 8(由于最左一位是符号位,不列入模中),对 − 3 -3 −3 取补得到 − 5 -5 −5(采用补码编码:1011)。
得到 8 = ∣ − 3 ∣ + ∣ − 5 ∣ 8 = |-3| + |-5| 8=∣−3∣+∣−5∣。
Derivation 推导:
首先假设现在以 n n n 位二进制位来存储数据,其中最左一位为符号位,那么模则是 2 n − 1 2^n - 1 2n−1。然后以 a a a 表示某正整数, b b b 表示某负整数,并且 c c c 为 b b b 的补数。
- 整理出 b ≡ c ( m o d 2 n − 1 ) b \equiv c \pmod{2^n - 1} b≡c(mod2n−1), a ≡ a ( m o d 2 n − 1 ) a \equiv a \pmod{2^n - 1} a≡a(mod2n−1)
- 根据补数式相加得到 a + b ≡ a + c ( m o d 2 n − 1 ) a + b \equiv a + c \pmod{2^n - 1} a+b≡a+c(mod2n−1)
- 即 mod ( a + b , 2 n − 1 ) = mod ( a + c , 2 n − 1 ) \text{mod}(a+b, 2^n - 1) = \text{mod}(a+c, 2^n - 1) mod(a+b,2n−1)=mod(a+c,2n−1)
- 回顾模的定义 “模,是指一个计量系统的计数范围,而模则是产生 “溢出” 的量”,可知当运算过程中产生 “溢出” 操作,实质上就是执行取模运算。而我们的存储空间是固定为 n n n 位二进制位,因此运算的最后一步默认就是取模运算。因此 a + b a+b a+b 与 a + c a+c a+c 在存储空间固定的前提下,最终结果必然相等。
上面已经证明了以补数来实现减法加法化,以正数表示负数的有效性。那下面我们来看看将原码转换为补码的规则为什么是成立的。
假设以 n n n 位二进制位来存储数据,其中最左一位为符号位
模 = 2 n − 1 = 1 + 1 ⋅ 2 + 1 ⋅ 2 2 + … + 1 ⋅ 2 n − 2 + 1 2^n - 1 = 1 + 1 \cdot 2 + 1 \cdot 2^2 + \ldots + 1 \cdot 2^{n-2} + 1 2n−1=1+1⋅2+1⋅22+…+1⋅2n−2+1
某负数原码 a = k 0 + k 1 ⋅ 2 + k 2 ⋅ 2 2 + … + k n − 2 ⋅ 2 n − 2 a = k_0 + k_1 \cdot 2 + k_2 \cdot 2^2 + \ldots + k_{n-2} \cdot 2^{n-2} a=k0+k1⋅2+k2⋅22+…+kn−2⋅2n−2
根据 “互为补数的绝对值相加等于模数:若 a ≡ b ( m o d m ) a \equiv b \pmod{m} a≡b(modm),则 m = ∣ a ∣ + ∣ b ∣ m = |a| + |b| m=∣a∣+∣b∣”
a a a 的补码 = 2 n − 1 − a = ( 1 − k 0 ) + ( 1 − k 1 ) ⋅ 2 + ( 1 − k 2 ) ⋅ 2 2 + … + ( 1 − k n − 2 ) ⋅ 2 n − 2 + 1 2^n - 1 - a = (1 - k_0) + (1 - k_1) \cdot 2 + (1 - k_2) \cdot 2^2 + \ldots + (1 - k_{n-2}) \cdot 2^{n-2} + 1 2n−1−a=(1−k0)+(1−k1)⋅2+(1−k2)⋅22+…+(1−kn−2)⋅2n−2+1
由于 k 0 , k 1 , … k_0, k_1, \ldots k0,k1,… 的值不是 0 就是 1,因此等价于作取反操作,然后最后再加 1。
Conclusion 结论:
ANSI C 标准中并没有规定必须用补码来表示有符号整数,但几乎所有实现都采用补码的表示方式。而 Java 则规定采用补码表示有符号整数。
本文尝试以相对全面的角度描述原码、反码和补码,若有纰漏请给位指正。
via:
-
JS魔法堂:彻底理解0.1 + 0.2 === 0.30000000000000004的背后 - _肥仔John - 博客园 posted @ 2016-01-16 14:40
https://www.cnblogs.com/fsjohnhuang/p/5115672.html -
基础野:细说浮点数 - _肥仔 John - 博客园 posted @ 2016-01-09 11:02
-
基础野:细说有符号整数 - _肥仔 John - 博客园 posted @ 2015-12-29 15:44
-
基础野:细说无符号整数 - _肥仔 John - 博客园 posted @ 2015-12-28 15:45
-
基础野:细说原码、反码和补码 - _肥仔 John - 博客园 posted @ 2015-12-21 14:05






















 390
390

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








