注:本文为“三角函数公式”相关文章合辑。
图片清晰度受引文原图所限。
英文引文,机翻未校。
中文引文,略作重排。
未整理去重,如有内容异常,请看原文。
三角函数公式总结
一、诱导公式
诱导公式用于将任意角的三角函数转化为锐角三角函数,核心规律为 “奇变偶不变,符号看象限”( k ∈ Z k \in \mathbb{Z} k∈Z)。
1. 终边相同的角(公式一)
设
α
\alpha
α 为任意角,终边相同的角的同一三角函数值相等:
sin
(
2
k
π
+
α
)
=
sin
α
cos
(
2
k
π
+
α
)
=
cos
α
tan
(
2
k
π
+
α
)
=
tan
α
cot
(
2
k
π
+
α
)
=
cot
α
\begin{align*} \sin(2k\pi + \alpha) &= \sin\alpha \\ \cos(2k\pi + \alpha) &= \cos\alpha \\ \tan(2k\pi + \alpha) &= \tan\alpha \\ \cot(2k\pi + \alpha) &= \cot\alpha \end{align*}
sin(2kπ+α)cos(2kπ+α)tan(2kπ+α)cot(2kπ+α)=sinα=cosα=tanα=cotα
2. π ± α \pi \pm \alpha π±α 的三角函数值(公式二、四)
-
π
+
α
\pi + \alpha
π+α:
sin ( π + α ) = − sin α cos ( π + α ) = − cos α tan ( π + α ) = tan α cot ( π + α ) = cot α \begin{align*} \sin(\pi + \alpha) &= -\sin\alpha \\ \cos(\pi + \alpha) &= -\cos\alpha \\ \tan(\pi + \alpha) &= \tan\alpha \\ \cot(\pi + \alpha) &= \cot\alpha \end{align*} sin(π+α)cos(π+α)tan(π+α)cot(π+α)=−sinα=−cosα=tanα=cotα -
π
−
α
\pi - \alpha
π−α:
sin ( π − α ) = sin α cos ( π − α ) = − cos α tan ( π − α ) = − tan α cot ( π − α ) = − cot α \begin{align*} \sin(\pi - \alpha) &= \sin\alpha \\ \cos(\pi - \alpha) &= -\cos\alpha \\ \tan(\pi - \alpha) &= -\tan\alpha \\ \cot(\pi - \alpha) &= -\cot\alpha \end{align*} sin(π−α)cos(π−α)tan(π−α)cot(π−α)=sinα=−cosα=−tanα=−cotα
3. − α -\alpha −α 与 2 π − α 2\pi - \alpha 2π−α 的三角函数值(公式三、五)
-
−
α
-\alpha
−α:
sin ( − α ) = − sin α cos ( − α ) = cos α tan ( − α ) = − tan α cot ( − α ) = − cot α \begin{align*} \sin(-\alpha) &= -\sin\alpha \\ \cos(-\alpha) &= \cos\alpha \\ \tan(-\alpha) &= -\tan\alpha \\ \cot(-\alpha) &= -\cot\alpha \end{align*} sin(−α)cos(−α)tan(−α)cot(−α)=−sinα=cosα=−tanα=−cotα -
2
π
−
α
2\pi - \alpha
2π−α(利用公式一和公式三):
sin ( 2 π − α ) = − sin α cos ( 2 π − α ) = cos α tan ( 2 π − α ) = − tan α cot ( 2 π − α ) = − cot α \begin{align*} \sin(2\pi - \alpha) &= -\sin\alpha \\ \cos(2\pi - \alpha) &= \cos\alpha \\ \tan(2\pi - \alpha) &= -\tan\alpha \\ \cot(2\pi - \alpha) &= -\cot\alpha \end{align*} sin(2π−α)cos(2π−α)tan(2π−α)cot(2π−α)=−sinα=cosα=−tanα=−cotα
4. π 2 ± α \frac{\pi}{2} \pm \alpha 2π±α 及 3 π 2 ± α \frac{3\pi}{2} \pm \alpha 23π±α 的三角函数值(公式六)
-
π
2
+
α
\frac{\pi}{2} + \alpha
2π+α:
sin ( π 2 + α ) = cos α cos ( π 2 + α ) = − sin α tan ( π 2 + α ) = − cot α cot ( π 2 + α ) = − tan α \begin{align*} \sin\left(\frac{\pi}{2} + \alpha\right) &= \cos\alpha \\ \cos\left(\frac{\pi}{2} + \alpha\right) &= -\sin\alpha \\ \tan\left(\frac{\pi}{2} + \alpha\right) &= -\cot\alpha \\ \cot\left(\frac{\pi}{2} + \alpha\right) &= -\tan\alpha \end{align*} sin(2π+α)cos(2π+α)tan(2π+α)cot(2π+α)=cosα=−sinα=−cotα=−tanα -
π
2
−
α
\frac{\pi}{2} - \alpha
2π−α:
sin ( π 2 − α ) = cos α cos ( π 2 − α ) = sin α tan ( π 2 − α ) = cot α cot ( π 2 − α ) = tan α \begin{align*} \sin\left(\frac{\pi}{2} - \alpha\right) &= \cos\alpha \\ \cos\left(\frac{\pi}{2} - \alpha\right) &= \sin\alpha \\ \tan\left(\frac{\pi}{2} - \alpha\right) &= \cot\alpha \\ \cot\left(\frac{\pi}{2} - \alpha\right) &= \tan\alpha \end{align*} sin(2π−α)cos(2π−α)tan(2π−α)cot(2π−α)=cosα=sinα=cotα=tanα -
3
π
2
+
α
\frac{3\pi}{2} + \alpha
23π+α:
sin ( 3 π 2 + α ) = − cos α cos ( 3 π 2 + α ) = − sin α tan ( 3 π 2 + α ) = − cot α cot ( 3 π 2 + α ) = − tan α \begin{align*} \sin\left(\frac{3\pi}{2} + \alpha\right) &= -\cos\alpha \\ \cos\left(\frac{3\pi}{2} + \alpha\right) &= -\sin\alpha \\ \tan\left(\frac{3\pi}{2} + \alpha\right) &= -\cot\alpha \\ \cot\left(\frac{3\pi}{2} + \alpha\right) &= -\tan\alpha \end{align*} sin(23π+α)cos(23π+α)tan(23π+α)cot(23π+α)=−cosα=−sinα=−cotα=−tanα -
3
π
2
−
α
\frac{3\pi}{2} - \alpha
23π−α:
sin ( 3 π 2 − α ) = − cos α cos ( 3 π 2 − α ) = − sin α tan ( 3 π 2 − α ) = cot α cot ( 3 π 2 − α ) = tan α \begin{align*} \sin\left(\frac{3\pi}{2} - \alpha\right) &= -\cos\alpha \\ \cos\left(\frac{3\pi}{2} - \alpha\right) &= -\sin\alpha \\ \tan\left(\frac{3\pi}{2} - \alpha\right) &= \cot\alpha \\ \cot\left(\frac{3\pi}{2} - \alpha\right) &= \tan\alpha \end{align*} sin(23π−α)cos(23π−α)tan(23π−α)cot(23π−α)=−cosα=−sinα=cotα=tanα
记忆口诀
- 奇变偶不变:当 k k k 为奇数时,函数名变为余函数(如 sin → cos \sin \to \cos sin→cos);当 k k k 为偶数时,函数名不变。
- 符号看象限:将 α \alpha α 视为锐角,原函数在对应象限的符号即为结果符号。
二、同角三角函数基本关系
1. 倒数关系
tan α ⋅ cot α = 1 sin α ⋅ csc α = 1 cos α ⋅ sec α = 1 \begin{align*} \tan\alpha \cdot \cot\alpha &= 1 \\ \sin\alpha \cdot \csc\alpha &= 1 \\ \cos\alpha \cdot \sec\alpha &= 1 \end{align*} tanα⋅cotαsinα⋅cscαcosα⋅secα=1=1=1
2. 商数关系
sin α cos α = tan α = sec α csc α cos α sin α = cot α = csc α sec α \begin{align*} \frac{\sin\alpha}{\cos\alpha} &= \tan\alpha = \frac{\sec\alpha}{\csc\alpha} \\ \\ \frac{\cos\alpha}{\sin\alpha} &= \cot\alpha = \frac{\csc\alpha}{\sec\alpha} \end{align*} cosαsinαsinαcosα=tanα=cscαsecα=cotα=secαcscα
3. 平方关系
sin 2 α + cos 2 α = 1 1 + tan 2 α = sec 2 α 1 + cot 2 α = csc 2 α \begin{align*} \sin^2\alpha + \cos^2\alpha &= 1 \\ 1 + \tan^2\alpha &= \sec^2\alpha \\ 1 + \cot^2\alpha &= \csc^2\alpha \end{align*} sin2α+cos2α1+tan2α1+cot2α=1=sec2α=csc2α
六角形记忆法
构造正六边形模型(上弦、中切、下割;左正、右余、中间 1 1 1):
- 倒数关系:对角线上两函数互为倒数。
- 商数关系:任一顶点函数值等于相邻两顶点函数值的乘积。
- 平方关系:阴影三角形中,上两顶点函数值的平方和等于下顶点函数值的平方。
三、两角和差公式
1. 两角和与差的正弦、余弦、正切
sin ( α + β ) = sin α cos β + cos α sin β sin ( α − β ) = sin α cos β − cos α sin β cos ( α + β ) = cos α cos β − sin α sin β cos ( α − β ) = cos α cos β + sin α sin β tan ( α + β ) = tan α + tan β 1 − tan α tan β tan ( α − β ) = tan α − tan β 1 + tan α tan β \begin{align*} \sin(\alpha + \beta) &= \sin\alpha\cos\beta + \cos\alpha\sin\beta \\ \sin(\alpha - \beta) &= \sin\alpha\cos\beta - \cos\alpha\sin\beta \\ \cos(\alpha + \beta) &= \cos\alpha\cos\beta - \sin\alpha\sin\beta \\ \cos(\alpha - \beta) &= \cos\alpha\cos\beta + \sin\alpha\sin\beta \\ \tan(\alpha + \beta) &= \frac{\tan\alpha + \tan\beta}{1 - \tan\alpha\tan\beta} \\ \tan(\alpha - \beta) &= \frac{\tan\alpha - \tan\beta}{1 + \tan\alpha\tan\beta} \end{align*} sin(α+β)sin(α−β)cos(α+β)cos(α−β)tan(α+β)tan(α−β)=sinαcosβ+cosαsinβ=sinαcosβ−cosαsinβ=cosαcosβ−sinαsinβ=cosαcosβ+sinαsinβ=1−tanαtanβtanα+tanβ=1+tanαtanβtanα−tanβ
四、倍角公式
1. 二倍角公式(升幂缩角)
sin 2 α = 2 sin α cos α cos 2 α = cos 2 α − sin 2 α = 2 cos 2 α − 1 = 1 − 2 sin 2 α tan 2 α = 2 tan α 1 − tan 2 α \begin{align*} \sin2\alpha &= 2\sin\alpha\cos\alpha \\ \cos2\alpha &= \cos^2\alpha - \sin^2\alpha = 2\cos^2\alpha - 1 = 1 - 2\sin^2\alpha \\ \tan2\alpha &= \frac{2\tan\alpha}{1 - \tan^2\alpha} \end{align*} sin2αcos2αtan2α=2sinαcosα=cos2α−sin2α=2cos2α−1=1−2sin2α=1−tan2α2tanα
2. 半角公式(降幂扩角)
sin 2 α 2 = 1 − cos α 2 cos 2 α 2 = 1 + cos α 2 tan 2 α 2 = 1 − cos α 1 + cos α tan α 2 = 1 − cos α sin α = sin α 1 + cos α \begin{align*} \sin^2\frac{\alpha}{2} &= \frac{1 - \cos\alpha}{2} \\ \cos^2\frac{\alpha}{2} &= \frac{1 + \cos\alpha}{2} \\ \tan^2\frac{\alpha}{2} &= \frac{1 - \cos\alpha}{1 + \cos\alpha} \\ \tan\frac{\alpha}{2} &= \frac{1 - \cos\alpha}{\sin\alpha} = \frac{\sin\alpha}{1 + \cos\alpha} \end{align*} sin22αcos22αtan22αtan2α=21−cosα=21+cosα=1+cosα1−cosα=sinα1−cosα=1+cosαsinα
3. 万能公式
sin
α
=
2
tan
α
2
1
+
tan
2
α
2
cos
α
=
1
−
tan
2
α
2
1
+
tan
2
α
2
tan
α
=
2
tan
α
2
1
−
tan
2
α
2
\begin{align*} \sin\alpha &= \frac{2\tan\frac{\alpha}{2}}{1 + \tan^2\frac{\alpha}{2}} \\ \cos\alpha &= \frac{1 - \tan^2\frac{\alpha}{2}}{1 + \tan^2\frac{\alpha}{2}} \\ \tan\alpha &= \frac{2\tan\frac{\alpha}{2}}{1 - \tan^2\frac{\alpha}{2}} \end{align*}
sinαcosαtanα=1+tan22α2tan2α=1+tan22α1−tan22α=1−tan22α2tan2α
推导思路:利用
sin
2
α
=
2
tan
α
1
+
tan
2
α
\sin2\alpha = \frac{2\tan\alpha}{1 + \tan^2\alpha}
sin2α=1+tan2α2tanα,将
α
\alpha
α 替换为
α
2
\frac{\alpha}{2}
2α 即可。
4. 三倍角公式
sin 3 α = 3 sin α − 4 sin 3 α cos 3 α = 4 cos 3 α − 3 cos α tan 3 α = 3 tan α − tan 3 α 1 − 3 tan 2 α \begin{align*} \sin3\alpha &= 3\sin\alpha - 4\sin^3\alpha \\ \cos3\alpha &= 4\cos^3\alpha - 3\cos\alpha \\ \tan3\alpha &= \frac{3\tan\alpha - \tan^3\alpha}{1 - 3\tan^2\alpha} \end{align*} sin3αcos3αtan3α=3sinα−4sin3α=4cos3α−3cosα=1−3tan2α3tanα−tan3α
五、和差化积与积化和差公式
1. 和差化积公式
sin α + sin β = 2 sin α + β 2 cos α − β 2 sin α − sin β = 2 cos α + β 2 sin α − β 2 cos α + cos β = 2 cos α + β 2 cos α − β 2 cos α − cos β = − 2 sin α + β 2 sin α − β 2 \begin{align*} \sin\alpha + \sin\beta &= 2\sin\frac{\alpha + \beta}{2}\cos\frac{\alpha - \beta}{2} \\ \sin\alpha - \sin\beta &= 2\cos\frac{\alpha + \beta}{2}\sin\frac{\alpha - \beta}{2} \\ \cos\alpha + \cos\beta &= 2\cos\frac{\alpha + \beta}{2}\cos\frac{\alpha - \beta}{2} \\ \cos\alpha - \cos\beta &= -2\sin\frac{\alpha + \beta}{2}\sin\frac{\alpha - \beta}{2} \end{align*} sinα+sinβsinα−sinβcosα+cosβcosα−cosβ=2sin2α+βcos2α−β=2cos2α+βsin2α−β=2cos2α+βcos2α−β=−2sin2α+βsin2α−β
2. 积化和差公式
sin
α
cos
β
=
1
2
[
sin
(
α
+
β
)
+
sin
(
α
−
β
)
]
cos
α
sin
β
=
1
2
[
sin
(
α
+
β
)
−
sin
(
α
−
β
)
]
cos
α
cos
β
=
1
2
[
cos
(
α
+
β
)
+
cos
(
α
−
β
)
]
sin
α
sin
β
=
−
1
2
[
cos
(
α
+
β
)
−
cos
(
α
−
β
)
]
\begin{align*} \sin\alpha\cos\beta &= \frac{1}{2}[\sin(\alpha + \beta) + \sin(\alpha - \beta)] \\ \cos\alpha\sin\beta &= \frac{1}{2}[\sin(\alpha + \beta) - \sin(\alpha - \beta)] \\ \cos\alpha\cos\beta &= \frac{1}{2}[\cos(\alpha + \beta) + \cos(\alpha - \beta)] \\ \sin\alpha\sin\beta &= -\frac{1}{2}[\cos(\alpha + \beta) - \cos(\alpha - \beta)] \end{align*}
sinαcosβcosαsinβcosαcosβsinαsinβ=21[sin(α+β)+sin(α−β)]=21[sin(α+β)−sin(α−β)]=21[cos(α+β)+cos(α−β)]=−21[cos(α+β)−cos(α−β)]
推导技巧:通过
sin
(
a
±
b
)
\sin(a \pm b)
sin(a±b) 和
cos
(
a
±
b
)
\cos(a \pm b)
cos(a±b) 的和差公式联立,再用
x
=
α
+
β
x = \alpha + \beta
x=α+β,
y
=
α
−
β
y = \alpha - \beta
y=α−β 换元得到。
六、三角函数在各象限的符号
象限符号口诀
- 第一象限:全正( sin + , cos + , tan + , cot + \sin+, \cos+, \tan+, \cot+ sin+,cos+,tan+,cot+)
- 第二象限:正弦正( sin + , cos − , tan − , cot − \sin+, \cos-, \tan-, \cot- sin+,cos−,tan−,cot−)
- 第三象限:切函数正( sin − , cos − , tan + , cot + \sin-, \cos-, \tan+, \cot+ sin−,cos−,tan+,cot+)
- 第四象限:余弦正( sin − , cos + , tan − , cot − \sin-, \cos+, \tan-, \cot- sin−,cos+,tan−,cot−)
符号表格
| 函数 | 第一象限 | 第二象限 | 第三象限 | 第四象限 |
|---|---|---|---|---|
| sin \sin sin | + + + | + + + | − - − | − - − |
| cos \cos cos | + + + | − - − | − - − | + + + |
| tan \tan tan | + + + | − - − | + + + | − - − |
| cot \cot cot | + + + | − - − | + + + | − - − |
用魔法六边形巧记三角恒等式
lvximing 发布于 2023-04-30 11:42・内蒙古
 [.](https://i-blog.csdnimg.cn/img_convert/d8ce1855695809ec2067e7985e4338e7.png =700x)
[.](https://i-blog.csdnimg.cn/img_convert/d8ce1855695809ec2067e7985e4338e7.png =700x)
本文将介绍一种借助“上弦、中切、下割;左正、右余、中间 1”的魔法六边形记忆三角恒等式的方法与技巧。
魔法六边形记忆法要点包括:
- 对角线上两个顶点的函数值互为倒数
- 倒三角中两上端点平方和等于下端点平方
- 任意一顶点的三角函数值等于与该点相邻的两个端点的三角函数值的乘积
这种记忆法可以帮助学生更好地理解和记忆三角函数恒等式,并提高学习效率。
1. 魔法六边形概述
1.1 魔法六边形简介
魔法六边形记忆法(Mnemonics in trigonometry)是一种通过六边形进行记忆三角函数运算规则的方法。其特征为“上弦中切下割,左正右余 1 中间”。
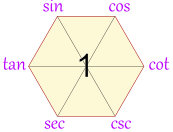
1.2 魔法六边形要义
- 对角线:对角线上两个顶点的函数值互为倒数;
- 倒三角:倒三角中两上端点平方和等于下端点平方;
- 邻点积:任意一顶点的三角函数值等于与该点相邻的两个端点的三角函数值的乘积。
2. 巧记三角恒等式
2.1 积型恒等式
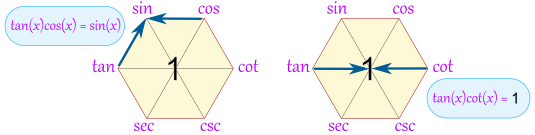
2.1.1 对角线乘积 = 1
sin ( x ) csc ( x ) = 1 \sin(x) \csc(x) = 1 sin(x)csc(x)=1
cos ( x ) sec ( x ) = 1 \cos(x) \sec(x) = 1 cos(x)sec(x)=1
cot ( x ) tan ( x ) = 1 \cot(x) \tan(x) = 1 cot(x)tan(x)=1
csc ( x ) sin ( x ) = 1 \csc(x) \sin(x) = 1 csc(x)sin(x)=1
sec ( x ) cos ( x ) = 1 \sec(x) \cos(x) = 1 sec(x)cos(x)=1
tan ( x ) cot ( x ) = 1 \tan(x) \cot(x) = 1 tan(x)cot(x)=1
2.1.2 中间顶点等于两边顶点的积
tan x = sin x sec x \tan x = \sin x \sec x tanx=sinxsecx
sin x = cos x tan x \sin x = \cos x \tan x sinx=cosxtanx
cos x = sin x cot x \cos x = \sin x \cot x cosx=sinxcotx
cot x = cos x csc x \cot x = \cos x \csc x cotx=cosxcscx
csc x = cot x sec x \csc x = \cot x \sec x cscx=cotxsecx
sec x = csc x tan x \sec x = \csc x \tan x secx=cscxtanx
2.2 商型恒等式
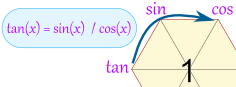
2.2.1 顺时针:任意一点的值等于这一点顺时针的第一个值与第二个值的比值
tan ( x ) = sin ( x ) cos ( x ) \tan(x) = \frac{\sin(x)}{\cos(x)} tan(x)=cos(x)sin(x)
sin ( x ) = cos ( x ) cot ( x ) \sin(x) = \frac{\cos(x)}{\cot(x)} sin(x)=cot(x)cos(x)
cos ( x ) = cot ( x ) csc ( x ) \cos(x) = \frac{\cot(x)}{\csc(x)} cos(x)=csc(x)cot(x)
cot ( x ) = csc ( x ) sec ( x ) \cot(x) = \frac{\csc(x)}{\sec(x)} cot(x)=sec(x)csc(x)
csc ( x ) = sec ( x ) tan ( x ) \csc(x) = \frac{\sec(x)}{\tan(x)} csc(x)=tan(x)sec(x)
sec ( x ) = tan ( x ) sin ( x ) \sec(x) = \frac{\tan(x)}{\sin(x)} sec(x)=sin(x)tan(x)
2.2.2 逆时针:任意一点的值等于这一点逆时针的第一个值与第二个值的比值
cos ( x ) = sin ( x ) tan ( x ) \cos(x) = \frac{\sin(x)}{\tan(x)} cos(x)=tan(x)sin(x)
sin ( x ) = tan ( x ) sec ( x ) \sin(x) = \frac{\tan(x)}{\sec(x)} sin(x)=sec(x)tan(x)
tan ( x ) = sec ( x ) csc ( x ) \tan(x) = \frac{\sec(x)}{\csc(x)} tan(x)=csc(x)sec(x)
sec ( x ) = csc ( x ) cot ( x ) \sec(x) = \frac{\csc(x)}{\cot(x)} sec(x)=cot(x)csc(x)
csc ( x ) = cot ( x ) cos ( x ) \csc(x) = \frac{\cot(x)}{\cos(x)} csc(x)=cos(x)cot(x)
cot ( x ) = cos ( x ) sin ( x ) \cot(x) = \frac{\cos(x)}{\sin(x)} cot(x)=sin(x)cos(x)
2.3 倒数恒等式
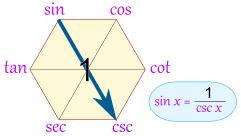
六边形中对角线上的两个三角函数互为“倒数”:
sin ( x ) = 1 csc ( x ) \sin(x) = \frac{1}{\csc(x)} sin(x)=csc(x)1
cos ( x ) = 1 sec ( x ) \cos(x) = \frac{1}{\sec(x)} cos(x)=sec(x)1
cot ( x ) = 1 tan ( x ) \cot(x) = \frac{1}{\tan(x)} cot(x)=tan(x)1
csc ( x ) = 1 sin ( x ) \csc(x) = \frac{1}{\sin(x)} csc(x)=sin(x)1
sec ( x ) = 1 cos ( x ) \sec(x) = \frac{1}{\cos(x)} sec(x)=cos(x)1
tan ( x ) = 1 cot ( x ) \tan(x) = \frac{1}{\cot(x)} tan(x)=cot(x)1
2.4 勾股/平方恒等式
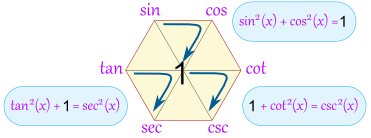
倒三角中两上端点平方和等于下端点平方:
sin 2 ( x ) + cos 2 ( x ) = 1 \sin^2(x) + \cos^2(x) = 1 sin2(x)+cos2(x)=1
1 + cot 2 ( x ) = csc 2 ( x ) 1 + \cot^2(x) = \csc^2(x) 1+cot2(x)=csc2(x)
tan 2 ( x ) + 1 = sec 2 ( x ) \tan^2(x) + 1 = \sec^2(x) tan2(x)+1=sec2(x)
2.5 互余恒等式
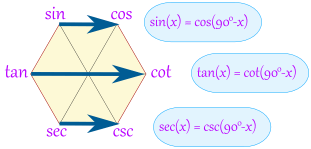
当两个角互余时,左端点某个角的三角函数值等于右端点在其余角处的三角函数值:
sin ( x ) = cos ( 9 0 ∘ − x ) \sin(x) = \cos(90^\circ - x) sin(x)=cos(90∘−x)
tan ( x ) = cot ( 9 0 ∘ − x ) \tan(x) = \cot(90^\circ - x) tan(x)=cot(90∘−x)
sec ( x ) = csc ( 9 0 ∘ − x ) \sec(x) = \csc(90^\circ - x) sec(x)=csc(90∘−x)
例如:
sin ( 3 0 ∘ ) = cos ( 6 0 ∘ ) \sin(30^\circ) = \cos(60^\circ) sin(30∘)=cos(60∘)
tan ( 8 0 ∘ ) = cot ( 1 0 ∘ ) \tan(80^\circ) = \cot(10^\circ) tan(80∘)=cot(10∘)
sec ( 4 0 ∘ ) = csc ( 5 0 ∘ ) \sec(40^\circ) = \csc(50^\circ) sec(40∘)=csc(50∘)
参考资料
[1] The Trigonometric Ratio Hexagon
[2] 三角恒等式的魔法六边形
https://www.shuxuele.com/algebra/trig-magic-hexagon.html
[3] 三角函数六边形记忆法_百度百科
https://baike.baidu.com/item/三角函数六边形记忆法
发布于 2023-04-30 11:42・内蒙古
Trigonometry Formulas
三角公式
June 24, 2019 by Veerendra
Trigonometry is a branch of mathematics that deal with angles, lengths and heights of triangles and relations between different parts of circles and other geometrical figures. Maths Formulas – Trigonometric Ratios and identities are very useful and learning the below formulae help in solving the problems better. Trigonometry formulas are essential for solving questions in Trigonometry Ratios and Identities in Competitive Exams.
三角学是数学的一个分支,涉及三角形的角度、长度和高度,以及圆和其他几何图形各部分之间的关系。数学公式——三角比和恒等式非常有用,学习下面的公式有助于更好地解决问题。三角公式对于在竞赛考试中解决三角比和恒等式问题至关重要。
Trigonometric Identities are equalities that involve trigonometric functions and are true for every value of the occurring variables where both sides of the equality are defined. Geometrically, these are identities involving certain functions of one or more angles.
三角恒等式是涉及三角函数的等式,对于等式两边都有定义的变量的每一个值,这些等式都成立。从几何上讲,这些是涉及一个或多个角度的某些函数的恒等式。
Trigonometric Ratio relationship between the measurement of the angles and the length of the side of the right triangle. These formulas relate lengths and areas of particular circles or triangles. On the next page you’ll find identities. The identities don’t refer to particular geometric figures but hold for all angles.
三角比是角度测量与直角三角形边长之间的关系。这些公式关联了特定圆或三角形的长度和面积。在下一页中,您将找到恒等式。这些恒等式并不针对特定的几何图形,而是对所有角度都成立。
Trigonometry Formulas
三角公式
Formulas for arcs and sectors of circles
圆的弧和扇形的公式
You can easily find both the length of an arc and the area of a sector for an angle
θ
\theta
θ in a circle of radius
r
r
r .
您可以轻松地找到半径为
r
r
r 的圆中角度
θ
\theta
θ 对应的弧长和扇形面积。
Length of an arc. The length of the arc is just the radius
r
r
r times the angle
θ
\theta
θ where the angle is measured in radians. To convert from degrees to radians, multiply the number of degrees by
π
180
\frac{\pi}{180}
180π .
弧长。弧长就是半径
r
r
r 乘以角度
θ
\theta
θ,其中角度以弧度为单位。要从度转换为弧度,将度数乘以
π
180
\frac{\pi}{180}
180π。
Arc
=
r
θ
= r \theta
=rθ .
弧长
Sector = 1 2 r 2 θ \text{Sector}=\frac{1}{2}{{r}^{2}}\theta Sector=21r2θ
Trigonometric Formulas Sector
Trigonometric Formulas – Right Angle
三角公式——直角
The most important formulas for trigonometry are those for a right triangle. If
θ
\theta
θ is one of the acute angles in a triangle, then the sine of theta is the ratio of the opposite side to the hypotenuse, the cosine is the ratio of the adjacent side to the hypotenuse, and the tangent is the ratio of the opposite side to the adjacent side.
三角学最重要的公式是直角三角形的公式。如果
θ
\theta
θ 是三角形中的一个锐角,那么
θ
\theta
θ 的正弦值是对边与斜边的比值,余弦值是邻边与斜边的比值,正切值是对边与邻边的比值。

三角公式勾股定理
Pythagorean theorem, the well-known geometric theorem that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse (the side opposite the right angle)—or, in familiar algebraic notation,
(
P
)
2
+
(
B
)
2
=
(
H
)
2
(P)^2 + (B)^2 = (H)^2
(P)2+(B)2=(H)2 .
勾股定理,众所周知的几何定理,直角三角形两直角边的平方和等于斜边的平方(斜边是直角对面的边)——或者,用熟悉的代数符号表示,
(
P
)
2
+
(
B
)
2
=
(
H
)
2
(P)^2 + (B)^2 = (H)^2
(P)2+(B)2=(H)2。
Applying Pythagoras theorem for the given right-angled theorem, we have:
应用勾股定理于给定的直角三角形,我们有:
(
Perpendicular
)
2
+
(
Base
)
2
=
(
Hypotenuse
)
2
( \text{Perpendicular} )^2 + ( \text{Base} )^2 = ( \text{Hypotenuse} )^2
(Perpendicular)2+(Base)2=(Hypotenuse)2
(
P
)
2
+
(
B
)
2
=
(
H
)
2
(P)^2 + (B)^2 = (H)^2
(P)2+(B)2=(H)2
The trigonometric properties are given below
三角性质如下
三角函数定义
| S.no | Property | Mathematical value |
|---|---|---|
| 1 | sin A \sin A sinA | P H \frac{P}{H} HP |
| 2 | cos A \cos A cosA | B H \frac{B}{H} HB |
| 3 | tan A \tan A tanA | P B \frac{P}{B} BP |
| 4 | cot A \cot A cotA | B P \frac{B}{P} PB |
| 5 | csc A \csc A cscA | H P \frac{H}{P} PH |
| 6 | sec A \sec A secA | H B \frac{H}{B} BH |
Relation Between Trigonometric Identities:
三角函数恒等式关系
| S.no | Identity | Relation |
|---|---|---|
| 1 | tan A \tan A tanA | sin A cos A \frac{\sin A}{\cos A} cosAsinA |
| 2 | cot A \cot A cotA | cos A sin A \frac{\cos A}{\sin A} sinAcosA |
| 3 | csc A \csc A cscA | 1 sin A \frac{1}{\sin A} sinA1 |
| 4 | sec A \sec A secA | 1 cos A \frac{1}{\cos A} cosA1 |
三角恒等式之间的关系 g
Magical Hexagon for Trigonometry Identities
三角恒等式的神奇六边形

神奇六边形三角公式
- Start with -
tan
(
x
)
=
sin
(
x
)
/
cos
(
x
)
\tan(x)=\sin(x)/\cos(x)
tan(x)=sin(x)/cos(x)
从 - tan ( x ) = sin ( x ) / cos ( x ) \tan(x)=\sin(x)/\cos(x) tan(x)=sin(x)/cos(x) 开始 -
cot
\cot
cot (which is cotangent) on the opposite side of the hexagon to
tan
\tan
tan
cot \cot cot(即 余切)在六边形中与 tan \tan tan 相对 -
csc
\csc
csc (which is cosecant) next, and
接下来是 csc \csc csc(即 余割),以及 -
sec
\sec
sec (which is secant) last
最后是 sec \sec sec(即 正割) - Important: the “co” functions are all on the right
重要提示:带“co”的函数都在右边
Magical Hexagon for Trig Identities
三角恒等式的神奇六边形 g
Clock Wise:
顺时针:

神奇六边形顺时针三角公式
- tan ( x ) = sin ( x ) cos ( x ) \tan(x) = \frac{\sin(x)}{\cos(x)} tan(x)=cos(x)sin(x)
- sin ( x ) = cos ( x ) cot ( x ) \sin(x) = \frac{\cos(x)}{\cot(x)} sin(x)=cot(x)cos(x)
- cos ( x ) = cot ( x ) csc ( x ) \cos(x) = \frac{\cot(x)}{\csc(x)} cos(x)=csc(x)cot(x)
- cot ( x ) = csc ( x ) sec ( x ) \cot(x) = \frac{\csc(x)}{\sec(x)} cot(x)=sec(x)csc(x)
- csc ( x ) = sec ( x ) tan ( x ) \csc(x) = \frac{\sec(x)}{\tan(x)} csc(x)=tan(x)sec(x)
- sec ( x ) = tan ( x ) sin ( x ) \sec(x) = \frac{\tan(x)}{\sin(x)} sec(x)=sin(x)tan(x)
Counterclock Wise:
逆时针:

神奇六边形逆时针三角公式
- cos ( x ) = sin ( x ) tan ( x ) \cos(x) = \frac{\sin(x)}{\tan(x)} cos(x)=tan(x)sin(x)
- sin ( x ) = tan ( x ) sec ( x ) \sin(x) = \frac{\tan(x)}{\sec(x)} sin(x)=sec(x)tan(x)
- tan ( x ) = sec ( x ) csc ( x ) \tan(x) = \frac{\sec(x)}{\csc(x)} tan(x)=csc(x)sec(x)
- sec ( x ) = csc ( x ) cot ( x ) \sec(x) = \frac{\csc(x)}{\cot(x)} sec(x)=cot(x)csc(x)
- csc ( x ) = cot ( x ) cos ( x ) \csc(x) = \frac{\cot(x)}{\cos(x)} csc(x)=cos(x)cot(x)
- cot ( x ) = cos ( x ) sin ( x ) \cot(x) = \frac{\cos(x)}{\sin(x)} cot(x)=sin(x)cos(x)
Reciprocal Relations
互为倒数的关系

互为倒数的三角公式 g
Trigonometric Formulas Reciprocal Relations
三角公式互为倒数的关系
csc
θ
=
1
sin
θ
\csc\theta=\frac{1}{\sin\theta}
cscθ=sinθ1
sec θ = 1 cos θ \sec\theta=\frac{1}{\cos\theta} secθ=cosθ1
cot θ = 1 tan θ \cot\theta=\frac{1}{\tan\theta} cotθ=tanθ1
sin θ = 1 csc θ \sin\theta=\frac{1}{\csc\theta} sinθ=cscθ1
cos θ = 1 sec θ \cos\theta=\frac{1}{\sec\theta} cosθ=secθ1
tan θ = 1 cot θ \tan\theta=\frac{1}{\cot\theta} tanθ=cotθ1
Square Law Formulas
平方法则公式

平方法则公式 g
sin 2 A + cos 2 A = 1 \sin^{2}A + \cos^{2}A = 1 sin2A+cos2A=1
tan 2 A + 1 = sec 2 A \tan^{2}A + 1=\sec^{2}A tan2A+1=sec2A
1 + cot 2 A = csc 2 1 + \cot^{2}A= \csc^{2} 1+cot2A=csc2
Trigonometric Formulas Square Law
三角公式平方法则
Along with the knowledge that the two acute angles are complementary, that is to say, they add to
9
0
∘
90^\circ
90∘, you can solve any right triangle:
除了知道两个锐角是互余的,即它们的和为
9
0
∘
90^\circ
90∘,您可以解任何直角三角形:
-
If you know two of the three sides, you can find the third side and both acute angles.
如果你知道三条边中的两条,你可以找到第三条边和两个锐角。 -
If you know one acute angle and one of the three sides, you can find the other acute angle and the other two sides.
如果你知道一个锐角和三条边中的一条,你可以找到另一个锐角和另外两条边。
*Signs of Trigonometric Ratios*
*三角比的符号*
A lot of trigonometry formulas are based on the signs of trigonometric ratios, based on the quadrants they lie in. Therefore it becomes extremely essential for us to understand how trigonometric ratios get the positive or negative sign. The sign is based on the quadrant in which the angle lies.
许多三角公式都基于三角比的符号,这些符号取决于它们所在的象限。因此,我们非常有必要理解三角比如何获得正号或负号。符号取决于角度所在的象限。
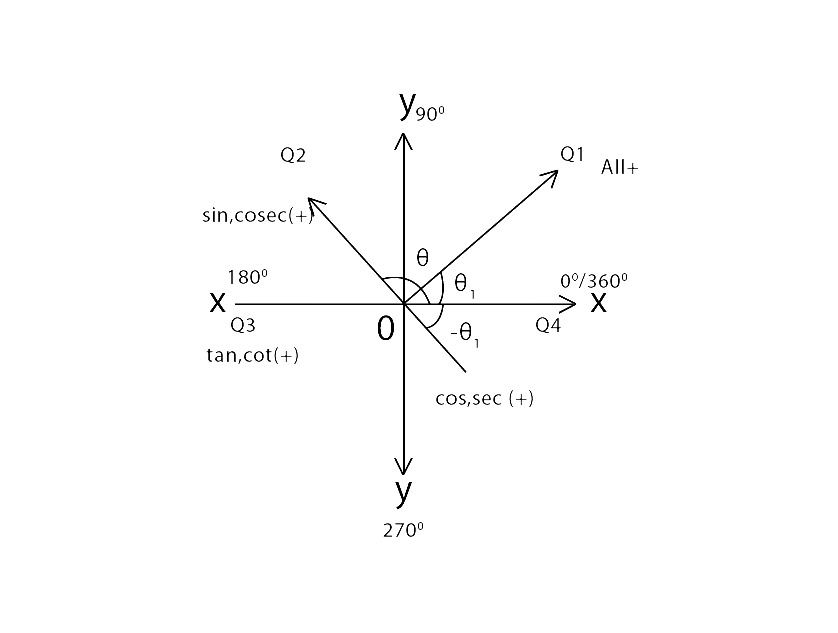
三角公式三角比的符号
Let us assume an angle of
θ
1
\theta_1
θ1 lying in the 1st quadrant and an angle
θ
\theta
θ in quadrant one and two combined. So let us see how signs change with respect to the quadrant they lie in.
假设一个角度
θ
1
\theta_1
θ1 位于第一象限,另一个角度
θ
\theta
θ 位于第一象限和第二象限的组合。那么我们来看看符号是如何随着它们所在的象限而变化的。
-
In Q 1 Q_1 Q1 all Trigonometric Ratios are positive. (Angles between 0 ∘ 0^\circ 0∘ – 9 0 ∘ 90^\circ 90∘)
在第一象限,所有三角比均为正。(角度在 0 ∘ 0^\circ 0∘ 到 9 0 ∘ 90^\circ 90∘ 之间)
-
In Q 2 Q_2 Q2 all trigonometric ratios of sin θ \sin \theta sinθ and csc θ \csc \theta cscθ are positive. (Angles between 9 0 ∘ 90^\circ 90∘ – 18 0 ∘ 180^\circ 180∘)
在第二象限, sin θ \sin \theta sinθ 和 csc θ \csc \theta cscθ 的三角比为正。(角度在 9 0 ∘ 90^\circ 90∘ 到 18 0 ∘ 180^\circ 180∘ 之间)
-
In Q 3 Q_3 Q3 all trigonometric ratios of cos θ \cos \theta cosθ and sec θ \sec \theta secθ are positive. (Angles between 18 0 ∘ 180^\circ 180∘ – 27 0 ∘ 270^\circ 270∘)
在第三象限, cos θ \cos \theta cosθ 和 sec θ \sec \theta secθ 的三角比为正。(角度在 18 0 ∘ 180^\circ 180∘ 到 27 0 ∘ 270^\circ 270∘ 之间)
-
In Q 4 Q_4 Q4 all trigonometric ratios of tan θ \tan \theta tanθ and cot θ \cot \theta cotθ are positive. (Angles between 27 0 ∘ 270^\circ 270∘ – 36 0 ∘ 360^\circ 360∘)
在第四象限, tan θ \tan \theta tanθ 和 cot θ \cot \theta cotθ 的三角比为正。(角度在 27 0 ∘ 270^\circ 270∘ 到 36 0 ∘ 360^\circ 360∘ 之间)
θ
\theta
θ is the angle made between the
x
x
x-axis and the line, in the anti-clockwise direction. If we move in the clockwise direction, the angle will be taken as
−
θ
- \theta
−θ. We know that in quadrant 4, only
cos
θ
\cos \theta
cosθ and
sec
θ
\sec \theta
secθ will be positive, the others will be negative, therefore:
θ
\theta
θ 是
x
x
x 轴与线之间的夹角,按逆时针方向测量。如果我们按顺时针方向移动,角度将被视为
−
θ
- \theta
−θ。我们知道在第四象限中,只有
cos
θ
\cos \theta
cosθ 和
sec
θ
\sec \theta
secθ 为正,其他为负,因此:
- sin ( − θ ) = − sin θ \sin ( - \theta ) = - \sin \theta sin(−θ)=−sinθ
- cos ( − θ ) = cos θ \cos ( - \theta ) = \cos \theta cos(−θ)=cosθ
- tan ( − θ ) = − tan θ \tan ( - \theta ) = - \tan \theta tan(−θ)=−tanθ
- sec ( − θ ) = + sec θ \sec ( - \theta ) = + \sec \theta sec(−θ)=+secθ
- cot ( − θ ) = − cot θ \cot ( - \theta ) = - \cot \theta cot(−θ)=−cotθ
We need to understand that trigonometric ratios would change for angles
9
0
∘
±
θ
90^\circ \pm \theta
90∘±θ and
27
0
∘
±
θ
270^\circ \pm \theta
270∘±θ and they will remain same for
18
0
∘
±
θ
180^\circ \pm \theta
180∘±θ and
36
0
∘
±
θ
360^\circ \pm \theta
360∘±θ. Let’s see what happens when we add or subtract
θ
\theta
θ from
9
0
∘
±
θ
90^\circ \pm \theta
90∘±θ and
27
0
∘
±
θ
270^\circ \pm \theta
270∘±θ:
我们需要理解,对于角度
9
0
∘
±
θ
90^\circ \pm \theta
90∘±θ 和
27
0
∘
±
θ
270^\circ \pm \theta
270∘±θ,三角比会发生变化,而对于
18
0
∘
±
θ
180^\circ \pm \theta
180∘±θ 和
36
0
∘
±
θ
360^\circ \pm \theta
360∘±θ,它们保持不变。让我们看看当我们从
9
0
∘
±
θ
90^\circ \pm \theta
90∘±θ 和
27
0
∘
±
θ
270^\circ \pm \theta
270∘±θ 中加减
θ
\theta
θ 时会发生什么。

三角公式勾股恒等式
- sec ( 9 0 ∘ + θ ) = csc θ \sec (90^\circ + \theta) = \csc \theta sec(90∘+θ)=cscθ
- cot ( 9 0 ∘ − θ ) = tan θ \cot (90^\circ - \theta) = \tan \theta cot(90∘−θ)=tanθ
- tan ( 9 0 ∘ + θ ) = − cot θ \tan (90^\circ + \theta) = -\cot \theta tan(90∘+θ)=−cotθ
- tan ( 9 0 ∘ − θ ) = cot θ \tan (90^\circ - \theta) = \cot \theta tan(90∘−θ)=cotθ
- sin ( 27 0 ∘ − θ ) = − cos θ \sin (270^\circ - \theta) = -\cos \theta sin(270∘−θ)=−cosθ
This is because any angle that is
27
0
∘
+
θ
270^\circ + \theta
270∘+θ will fall in quadrant 4 and in this quadrant only trigonometric ratios of
cos
\cos
cos and
sec
\sec
sec are positive. So the above will be negative.
27
0
∘
−
θ
270^\circ - \theta
270∘−θ will fall in the quadrant 3 and in this quadrant trigonometric ratios of
tan
\tan
tan and
cot
\cot
cot are positive, so it will again be negative. For
18
0
∘
±
θ
180^\circ \pm \theta
180∘±θ and for
36
0
∘
±
θ
360^\circ \pm \theta
360∘±θ, the signs will remain the same.
这是因为任何角度为
27
0
∘
+
θ
270^\circ + \theta
270∘+θ 的角都将落在第四象限,在这个象限中,只有
cos
\cos
cos 和
sec
\sec
sec 的三角比为正。因此,上述结果为负。
27
0
∘
−
θ
270^\circ - \theta
270∘−θ 将落在第三象限,在这个象限中,
tan
\tan
tan 和
cot
\cot
cot 的三角比为正,因此它也将为负。对于
18
0
∘
±
θ
180^\circ \pm \theta
180∘±θ 和
36
0
∘
±
θ
360^\circ \pm \theta
360∘±θ,符号保持不变。
- sin ( 36 0 ∘ + θ ) = sin θ \sin ( 360^\circ + \theta ) = \sin \theta sin(360∘+θ)=sinθ
- sin ( 36 0 ∘ − θ ) = − sin θ \sin ( 360^\circ - \theta ) = - \sin \theta sin(360∘−θ)=−sinθ
For
36
0
∘
+
θ
360^\circ + \theta
360∘+θ, the angle will complete one full rotation and then lie in quadrant 1 where all trigonometric ratios are positive. So there are 2 important things to remember:
对于
36
0
∘
+
θ
360^\circ + \theta
360∘+θ,角度将完成一个完整的旋转,然后位于第一象限,所有三角比均为正。因此,有两点需要记住:
-
The sign of the trigonometric ratios change based on the value of θ \theta θ.
三角比的符号根据 θ \theta θ 的值而变化。
-
sin \sin sin becomes cos \cos cos and cos \cos cos becomes sin \sin sin for 9 0 ∘ + θ 90^\circ + \theta 90∘+θ and for 27 0 ∘ + θ 270^\circ + \theta 270∘+θ and it remains the same for 18 0 ∘ + θ 180^\circ + \theta 180∘+θ and for 36 0 ∘ + θ 360^\circ + \theta 360∘+θ.
对于 9 0 ∘ + θ 90^\circ + \theta 90∘+θ 和 27 0 ∘ + θ 270^\circ + \theta 270∘+θ, sin \sin sin 变为 cos \cos cos, cos \cos cos 变为 sin \sin sin,而对于 18 0 ∘ + θ 180^\circ + \theta 180∘+θ 和 36 0 ∘ + θ 360^\circ + \theta 360∘+θ,它们保持不变。
Trigonometry Formulas | Trigonometric Identities
三角公式 | 三角恒等式
After looking at the trigonometric ratios, let us move on to trigonometric identities, which are the basics of most trigonometry formulas. The above identities hold true for any value of
θ
\theta
θ.
在研究了三角比之后,让我们转向三角恒等式,这些是大多数三角公式的基础。上述恒等式对于任何
θ
\theta
θ 的值都成立。
Product Identities:
乘积恒等式:

乘积恒等式三角公式
Trigonometry Formulas | Sum and Difference of Angles
三角公式 | 角的和与差
Trigonometry Formulas Converitng Products to Sum and difference
三角公式将乘积转换为和与差 g
sin A sin B = 1 2 [ cos ( A − B ) − cos ( A + B ) ] cos A cos B = 1 2 [ cos ( A − B ) + cos ( A + B ) ] sin A cos B = 1 2 [ sin ( A + B ) + sin ( A − B ) ] cos A sin B = 1 2 [ sin ( A + B ) − sin ( A − B ) ] \begin{align*} \sin A\sin B&=\frac{1}{2}[\cos(A - B)-\cos(A + B)] \\ \cos A\cos B&=\frac{1}{2}[\cos(A - B)+\cos(A + B)] \\ \sin A\cos B&=\frac{1}{2}[\sin(A + B)+\sin(A - B)] \\ \cos A\sin B&=\frac{1}{2}[\sin(A + B)-\sin(A - B)] \end{align*} sinAsinBcosAcosBsinAcosBcosAsinB=21[cos(A−B)−cos(A+B)]=21[cos(A−B)+cos(A+B)]=21[sin(A+B)+sin(A−B)]=21[sin(A+B)−sin(A−B)]
Trigonometry Formulas | Double Angle Formulas
三角公式 | 倍角公式
g
sin
2
θ
=
2
sin
θ
cos
θ
cos
2
θ
=
cos
2
θ
−
sin
2
θ
=
2
cos
2
θ
−
1
=
1
−
2
sin
2
θ
tan
2
θ
=
2
tan
θ
1
−
tan
2
θ
cot
2
θ
=
cot
2
θ
−
1
2
cot
θ
\begin{align*} \sin2\theta&=2\sin\theta\cos\theta\\ \cos2\theta&=\cos^{2}\theta - \sin^{2}\theta\\ &=2\cos^{2}\theta - 1\\ &=1 - 2\sin^{2}\theta\\ \tan2\theta&=\frac{2\tan\theta}{1 - \tan^{2}\theta}\\ \cot2\theta&=\frac{\cot^{2}\theta - 1}{2\cot\theta} \end{align*}
sin2θcos2θtan2θcot2θ=2sinθcosθ=cos2θ−sin2θ=2cos2θ−1=1−2sin2θ=1−tan2θ2tanθ=2cotθcot2θ−1
Trigonometry Formulas | Triple Angle Formulas
三角公式 | 三倍角公式
sin 3 θ = 3 sin θ − 4 sin 3 θ cos 3 θ = 4 cos 3 θ − 3 cos θ tan 3 θ = 3 tan θ − tan 3 θ 1 − 3 tan 2 θ cot 3 θ = cot 3 θ − 3 cot θ 3 cot 2 θ − 1 \begin{align*} \sin3\theta &= 3\sin\theta - 4\sin^{3}\theta \\ \cos3\theta &= 4\cos^{3}\theta - 3\cos\theta \\ \tan3\theta &= \frac{3\tan\theta - \tan^{3}\theta}{1 - 3\tan^{2}\theta} \\ \cot3\theta &= \frac{\cot^{3}\theta - 3\cot\theta}{3\cot^{2}\theta - 1} \end{align*} sin3θcos3θtan3θcot3θ=3sinθ−4sin3θ=4cos3θ−3cosθ=1−3tan2θ3tanθ−tan3θ=3cot2θ−1cot3θ−3cotθ
Trigonometry Formulas | Values of Trigonometric Ratios
三角公式 | 三角比的值
Trigonometric Values for some Common angles
g
| Degrees | Radians | sin θ \sin\theta sinθ | cos θ \cos\theta cosθ | tan θ \tan\theta tanθ | cot θ \cot\theta cotθ | sec θ \sec\theta secθ | csc θ \csc\theta cscθ |
|---|---|---|---|---|---|---|---|
| 0 ∘ 0^{\circ} 0∘ | 0 0 0 | 0 0 0 | 1 1 1 | 0 0 0 | Undefined | 1 1 1 | Undefined |
| 3 0 ∘ 30^{\circ} 30∘ | π 6 \frac{\pi}{6} 6π | 1 2 \frac{1}{2} 21 | 3 2 \frac{\sqrt{3}}{2} 23 | 1 3 \frac{1}{\sqrt{3}} 31 | 3 \sqrt{3} 3 | 2 3 \frac{2}{\sqrt{3}} 32 | 2 2 2 |
| 4 5 ∘ 45^{\circ} 45∘ | π 4 \frac{\pi}{4} 4π | 1 2 \frac{1}{\sqrt{2}} 21 | 1 2 \frac{1}{\sqrt{2}} 21 | 1 1 1 | 1 1 1 | 2 \sqrt{2} 2 | 2 \sqrt{2} 2 |
| 6 0 ∘ 60^{\circ} 60∘ | π 3 \frac{\pi}{3} 3π | 3 2 \frac{\sqrt{3}}{2} 23 | 1 2 \frac{1}{2} 21 | 3 \sqrt{3} 3 | 1 3 \frac{1}{\sqrt{3}} 31 | 2 2 2 | 2 3 \frac{2}{\sqrt{3}} 32 |
| 9 0 ∘ 90^{\circ} 90∘ | π 2 \frac{\pi}{2} 2π | 1 1 1 | 0 0 0 | Undefined | 0 0 0 | Undefined | 1 1 1 |
| 18 0 ∘ 180^{\circ} 180∘ | π \pi π | 0 0 0 | − 1 -1 −1 | 0 0 0 | Undefined | − 1 -1 −1 | Undefined |
| 36 0 ∘ 360^{\circ} 360∘ | 2 π 2\pi 2π | 0 0 0 | 1 1 1 | 0 0 0 | Undefined | 1 1 1 | Undefined |
Summary of Trigonometric Identities
三角恒等式总结

Periodicity and Periodic Identities
周期性和周期恒等式
sin ( θ + 2 π n ) = sin θ cos ( θ + 2 π n ) = cos θ tan ( θ + 2 π n ) = tan θ csc ( θ + 2 π n ) = csc θ sec ( θ + 2 π n ) = sec θ cot ( θ + 2 π n ) = cot θ \begin{align*} \sin(\theta + 2\pi n)&=\sin\theta\\ \cos(\theta + 2\pi n)&=\cos\theta\\ \tan(\theta + 2\pi n)&=\tan\theta\\ \csc(\theta + 2\pi n)&=\csc\theta\\ \sec(\theta + 2\pi n)&=\sec\theta\\ \cot(\theta + 2\pi n)&=\cot\theta \end{align*} sin(θ+2πn)cos(θ+2πn)tan(θ+2πn)csc(θ+2πn)sec(θ+2πn)cot(θ+2πn)=sinθ=cosθ=tanθ=cscθ=secθ=cotθ
Half angle identities
半角恒等式
sin x 2 = ± 1 − cos x 2 \sin \frac{x}{2} = \pm \sqrt{\frac{1 - \cos x}{2}} sin2x=±21−cosx
cos
x
2
=
±
1
+
cos
x
2
\cos \frac{x}{2} = \pm \sqrt{\frac{1 + \cos x}{2}}
cos2x=±21+cosx
tan
x
2
=
1
−
cos
x
1
+
cos
x
=
1
−
cos
x
sin
x
=
sin
x
1
+
cos
x
\tan \frac{x}{2} = \sqrt{\frac{1 - \cos x}{1 + \cos x}} = \frac{1 - \cos x}{\sin x} = \frac{\sin x}{1 + \cos x}
tan2x=1+cosx1−cosx=sinx1−cosx=1+cosxsinx
cot
x
2
=
1
+
cos
x
1
−
cos
x
=
1
+
cos
x
sin
x
=
sin
x
1
−
cos
x
\cot \frac{x}{2} = \sqrt{\frac{1 + \cos x}{1 - \cos x}} = \frac{1 + \cos x}{\sin x} = \frac{\sin x}{1 - \cos x}
cot2x=1−cosx1+cosx=sinx1+cosx=1−cosxsinx
Complex relations
复杂关系
sin θ = e i θ − e − i θ 2 i cos θ = e i θ + e − i θ 2 tan θ = e i θ − e − i θ ( e i θ + e − i θ ) i cot θ = ( e i θ + e − i θ ) i e i θ − e − i θ csc θ = 2 i e i θ − e − i θ sec θ = 2 e i θ + e − i θ \begin{align*} \sin\theta&=\frac{e^{i\theta}-e^{-i\theta}}{2i}\\ \cos\theta&=\frac{e^{i\theta}+e^{-i\theta}}{2}\\ \tan\theta&=\frac{e^{i\theta}-e^{-i\theta}}{(e^{i\theta}+e^{-i\theta})i}\\ \cot\theta&=\frac{(e^{i\theta}+e^{-i\theta})i}{e^{i\theta}-e^{-i\theta}}\\ \csc\theta&=\frac{2i}{e^{i\theta}-e^{-i\theta}}\\ \sec\theta&=\frac{2}{e^{i\theta}+e^{-i\theta}} \end{align*} sinθcosθtanθcotθcscθsecθ=2ieiθ−e−iθ=2eiθ+e−iθ=(eiθ+e−iθ)ieiθ−e−iθ=eiθ−e−iθ(eiθ+e−iθ)i=eiθ−e−iθ2i=eiθ+e−iθ2
三角公式复杂关系
Inverse trigonometric functions
反三角函数
| Name | Usual notation ~~~~ | Definition ~~~~~ | Domain of x x x for real result | Range of usual principal value (radians) | Range of usual principal value (degrees) |
|---|---|---|---|---|---|
| arcsine | y = arcsin ( x ) y = \arcsin(x) y=arcsin(x) | x = sin ( y ) x = \sin(y) x=sin(y) | − 1 ≤ x ≤ 1 -1\leq x\leq1 −1≤x≤1 | − π 2 ≤ y ≤ π 2 -\frac{\pi}{2}\leq y\leq\frac{\pi}{2} −2π≤y≤2π | − 9 0 ∘ ≤ y ≤ 9 0 ∘ -90^{\circ}\leq y\leq90^{\circ} −90∘≤y≤90∘ |
| arccosine | y = arccos ( x ) y = \arccos(x) y=arccos(x) | x = cos ( y ) x = \cos(y) x=cos(y) | − 1 ≤ x ≤ 1 -1\leq x\leq1 −1≤x≤1 | 0 ≤ y ≤ π 0\leq y\leq\pi 0≤y≤π | 0 ∘ ≤ y ≤ 18 0 ∘ 0^{\circ}\leq y\leq180^{\circ} 0∘≤y≤180∘ |
| arctangent | y = arctan ( x ) y = \arctan(x) y=arctan(x) | x = tan ( y ) x = \tan(y) x=tan(y) | all real numbers | − π 2 < y < π 2 -\frac{\pi}{2}<y<\frac{\pi}{2} −2π<y<2π | − 9 0 ∘ < y < 9 0 ∘ -90^{\circ}<y<90^{\circ} −90∘<y<90∘ |
| arccotangent | y = arccot ( x ) y = \text{arccot}(x) y=arccot(x) | x = cot ( y ) x = \cot(y) x=cot(y) | all real numbers | 0 < y < π 0<y<\pi 0<y<π | 0 ∘ < y < 18 0 ∘ 0^{\circ}<y<180^{\circ} 0∘<y<180∘ |
| arcsecant | y = arcsec ( x ) y = \text{arcsec}(x) y=arcsec(x) | x = sec ( y ) x = \sec(y) x=sec(y) | x ≤ − 1 x\leq - 1 x≤−1 or 1 ≤ x 1\leq x 1≤x | 0 ≤ y < π 2 0\leq y<\frac{\pi}{2} 0≤y<2π or π 2 < y ≤ π \frac{\pi}{2}<y\leq\pi 2π<y≤π | 0 ∘ ≤ y < 9 0 ∘ 0^{\circ}\leq y<90^{\circ} 0∘≤y<90∘ or 9 0 ∘ < y ≤ 18 0 ∘ 90^{\circ}<y\leq180^{\circ} 90∘<y≤180∘ |
| arccosecant | y = arccsc ( x ) y = \text{arccsc}(x) y=arccsc(x) | x = csc ( y ) x = \csc(y) x=csc(y) | x ≤ − 1 x\leq - 1 x≤−1 or 1 ≤ x 1\leq x 1≤x | − π 2 ≤ y < 0 -\frac{\pi}{2}\leq y<0 −2π≤y<0 or 0 < y ≤ π 2 0<y\leq\frac{\pi}{2} 0<y≤2π | − 9 0 ∘ ≤ y < 0 ∘ -90^{\circ}\leq y<0^{\circ} −90∘≤y<0∘ or 0 ∘ < y ≤ 9 0 ∘ 0^{\circ}<y\leq90^{\circ} 0∘<y≤90∘ |

三角公式反三角函数
Complimentary angle
余角
arcsin ( x ) = π 2 − arccos ( x ) arccos ( x ) = π 2 − arcsin ( x ) arctan ( x ) = π 2 − a r c c o t ( x ) a r c c o t ( x ) = π 2 − arctan ( x ) a r c c s c ( x ) = π 2 − a r c s e c ( x ) a r c s e c ( x ) = π 2 − a r c c s c ( x ) \begin{align*} \arcsin(x)&=\frac{\pi}{2}-\arccos(x)\\ \arccos(x)&=\frac{\pi}{2}-\arcsin(x)\\ \arctan(x)&=\frac{\pi}{2}-\mathrm{arccot}(x)\\ \mathrm{arccot}(x)&=\frac{\pi}{2}-\arctan(x)\\ \mathrm{arccsc}(x)&=\frac{\pi}{2}-\mathrm{arcsec}(x)\\ \mathrm{arcsec}(x)&=\frac{\pi}{2}-\mathrm{arccsc}(x) \end{align*} arcsin(x)arccos(x)arctan(x)arccot(x)arccsc(x)arcsec(x)=2π−arccos(x)=2π−arcsin(x)=2π−arccot(x)=2π−arctan(x)=2π−arcsec(x)=2π−arccsc(x)
三角公式余角
Negative arguments
负角公式
arcsin ( − x ) = − arcsin ( x ) arccos ( − x ) = π − arccos ( x ) arctan ( − x ) = − arctan ( x ) a r c c o t ( − x ) = π − a r c c o t ( x ) a r c s e c ( − x ) = π − a r c s e c ( x ) a r c c s c ( − x ) = − a r c c s c ( x ) \begin{align*} \arcsin(-x)&=-\arcsin(x)\\ \arccos(-x)&=\pi - \arccos(x)\\ \arctan(-x)&=-\arctan(x)\\ \mathrm{arccot}(-x)&=\pi - \mathrm{arccot}(x)\\ \mathrm{arcsec}(-x)&=\pi - \mathrm{arcsec}(x)\\ \mathrm{arccsc}(-x)&=-\mathrm{arccsc}(x) \end{align*} arcsin(−x)arccos(−x)arctan(−x)arccot(−x)arcsec(−x)arccsc(−x)=−arcsin(x)=π−arccos(x)=−arctan(x)=π−arccot(x)=π−arcsec(x)=−arccsc(x)
Reciprocal arguments
倒数公式
arccos ( 1 x ) = a r c s e c ( x ) arcsin ( 1 x ) = a r c c s c ( x ) arctan ( 1 x ) = { π 2 − arctan ( x ) = a r c c o t ( x ) , if x > 0 − π 2 − arctan ( x ) = a r c c o t ( x ) − π , if x < 0 a r c c o t ( 1 x ) = { π 2 − a r c c o t ( x ) = arctan ( x ) , if x > 0 3 π 2 − a r c c o t ( x ) = π + arctan ( x ) , if x < 0 a r c s e c ( 1 x ) = arccos ( x ) a r c c s c ( 1 x ) = arcsin ( x ) \begin{align*} \arccos\left(\frac{1}{x}\right)&=\mathrm{arcsec}(x)\\ \arcsin\left(\frac{1}{x}\right)&=\mathrm{arccsc}(x)\\ \arctan\left(\frac{1}{x}\right)&=\begin{cases} \frac{\pi}{2}-\arctan(x)=\mathrm{arccot}(x),& \text{if } x>0\\ -\frac{\pi}{2}-\arctan(x)=\mathrm{arccot}(x)-\pi, &\text{if } x<0 \end{cases}\\ \mathrm{arccot}\left(\frac{1}{x}\right)&=\begin{cases} \frac{\pi}{2}-\mathrm{arccot}(x)=\arctan(x),& \text{if } x>0\\ \frac{3\pi}{2}-\mathrm{arccot}(x)=\pi+\arctan(x), &\text{if } x<0 \end{cases}\\ \mathrm{arcsec}\left(\frac{1}{x}\right)&=\arccos(x)\\ \mathrm{arccsc}\left(\frac{1}{x}\right)&=\arcsin(x) \end{align*} arccos(x1)arcsin(x1)arctan(x1)arccot(x1)arcsec(x1)arccsc(x1)=arcsec(x)=arccsc(x)={2π−arctan(x)=arccot(x),−2π−arctan(x)=arccot(x)−π,if x>0if x<0={2π−arccot(x)=arctan(x),23π−arccot(x)=π+arctan(x),if x>0if x<0=arccos(x)=arcsin(x)
Values of Trigonometric Functions
三角函数的值
| α \alpha α | 0 0 0 | π 6 \frac{\pi}{6} 6π | π 4 \frac{\pi}{4} 4π | π 3 \frac{\pi}{3} 3π | π 2 \frac{\pi}{2} 2π | 2 π 3 \frac{2\pi}{3} 32π | 3 π 4 \frac{3\pi}{4} 43π | 5 π 6 \frac{5\pi}{6} 65π | π \pi π | 7 π 6 \frac{7\pi}{6} 67π | 5 π 4 \frac{5\pi}{4} 45π | 4 π 3 \frac{4\pi}{3} 34π | 3 π 2 \frac{3\pi}{2} 23π | 5 π 3 \frac{5\pi}{3} 35π | 7 π 4 \frac{7\pi}{4} 47π | 11 π 6 \frac{11\pi}{6} 611π | 2 π 2\pi 2π |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| α ∘ \alpha^{\circ} α∘ | 0 ∘ 0^{\circ} 0∘ | 3 0 ∘ 30^{\circ} 30∘ | 4 5 ∘ 45^{\circ} 45∘ | 6 0 ∘ 60^{\circ} 60∘ | 9 0 ∘ 90^{\circ} 90∘ | 12 0 ∘ 120^{\circ} 120∘ | 13 5 ∘ 135^{\circ} 135∘ | 15 0 ∘ 150^{\circ} 150∘ | 18 0 ∘ 180^{\circ} 180∘ | 21 0 ∘ 210^{\circ} 210∘ | 22 5 ∘ 225^{\circ} 225∘ | 24 0 ∘ 240^{\circ} 240∘ | 27 0 ∘ 270^{\circ} 270∘ | 30 0 ∘ 300^{\circ} 300∘ | 31 5 ∘ 315^{\circ} 315∘ | 33 0 ∘ 330^{\circ} 330∘ | 36 0 ∘ 360^{\circ} 360∘ |
| sin α \sin\alpha sinα | 0 0 0 | 1 2 \frac{1}{2} 21 | 2 2 \frac{\sqrt{2}}{2} 22 | 3 2 \frac{\sqrt{3}}{2} 23 | 1 1 1 | 3 2 \frac{\sqrt{3}}{2} 23 | 2 2 \frac{\sqrt{2}}{2} 22 | 1 2 \frac{1}{2} 21 | 0 0 0 | − 1 2 -\frac{1}{2} −21 | − 2 2 -\frac{\sqrt{2}}{2} −22 | − 3 2 -\frac{\sqrt{3}}{2} −23 | − 1 -1 −1 | − 3 2 -\frac{\sqrt{3}}{2} −23 | − 2 2 -\frac{\sqrt{2}}{2} −22 | − 1 2 -\frac{1}{2} −21 | 0 0 0 |
| cos α \cos\alpha cosα | 1 1 1 | 3 2 \frac{\sqrt{3}}{2} 23 | 2 2 \frac{\sqrt{2}}{2} 22 | 1 2 \frac{1}{2} 21 | 0 0 0 | − 1 2 -\frac{1}{2} −21 | − 2 2 -\frac{\sqrt{2}}{2} −22 | − 3 2 -\frac{\sqrt{3}}{2} −23 | − 1 -1 −1 | − 3 2 -\frac{\sqrt{3}}{2} −23 | − 2 2 -\frac{\sqrt{2}}{2} −22 | − 1 2 -\frac{1}{2} −21 | 0 0 0 | 1 2 \frac{1}{2} 21 | 2 2 \frac{\sqrt{2}}{2} 22 | 3 2 \frac{\sqrt{3}}{2} 23 | 1 1 1 |
| tg α \text{tg}\alpha tgα | 0 0 0 | 1 3 \frac{1}{\sqrt{3}} 31 | 1 1 1 | 3 \sqrt{3} 3 | - | − 3 -\sqrt{3} −3 | − 1 -1 −1 | − 1 3 -\frac{1}{\sqrt{3}} −31 | 0 0 0 | 1 3 \frac{1}{\sqrt{3}} 31 | 1 1 1 | 3 \sqrt{3} 3 | - | − 3 -\sqrt{3} −3 | − 1 -1 −1 | − 1 3 -\frac{1}{\sqrt{3}} −31 | 0 0 0 |
| ctg α \text{ctg}\alpha ctgα | - | 3 \sqrt{3} 3 | 1 1 1 | 1 3 \frac{1}{\sqrt{3}} 31 | 0 0 0 | − 1 3 -\frac{1}{\sqrt{3}} −31 | − 1 -1 −1 | − 3 -\sqrt{3} −3 | - | 3 \sqrt{3} 3 | 1 1 1 | 1 3 \frac{1}{\sqrt{3}} 31 | 0 0 0 | − 1 3 -\frac{1}{\sqrt{3}} −31 | − 1 -1 −1 | − 3 -\sqrt{3} −3 | - |
Filed Under: CBSE
Super magic Hexagon for Trigonometric identities Tricks
三角恒等式的超级魔法六边形技巧
~ Durai, Kugan
The super hexagon is a special diagram that helps the children to remember all the trigonometric identities and trigonometric functions visually [also requires memory].
超级六边形是一种特殊的图表,它可以帮助孩子们通过视觉记忆所有三角恒等式和三角函数(也需要记忆)。
How to draw the super hexogen
如何绘制超级六边形
Draw the hexagon and we need to join all the opposite vertices and place the value 1 in the center of the hexagon.
绘制六边形,并连接所有对角顶点,在六边形中心放置值 1。

Write the tan on the left vertex of the hexagon and use the quotient to identify the tangent ongoing clockwise, starting with
tan
=
sin
cos
\tan = \frac{\sin}{\cos}
tan=cossin.
在六边形的左顶点写上 tan,并使用商来标识顺时针方向的正切,从
tan
=
sin
cos
\tan = \frac{\sin}{\cos}
tan=cossin 开始。
Then add:
然后添加:
-
cot \cot cot (which is cotangent) on the opposite side of the hexagon to tan \tan tan
cot \cot cot(即余切)在六边形的对面,与 tan \tan tan 对应 -
csc \csc csc (which is cosecant) next, and
csc \csc csc(即正割)接下来, -
sec \sec sec (which is secant) last
sec \sec sec(即正割)最后
Fill the reciprocal identities on the opposite side. Now the super magic hexagon is ready
在对面填写倒数恒等式。现在超级魔法六边形已经准备好了。

Create Quotient identities
创建商恒等式
To understand the first set of formulae will let try around the hexagon in the clockwise direction, for the next set of directions will let try around the hexagon in the anti-clockwise direction.
为了理解第一组公式,让我们尝试围绕六边形顺时针方向进行,对于下一组方向,我们将尝试围绕六边形逆时针方向进行。

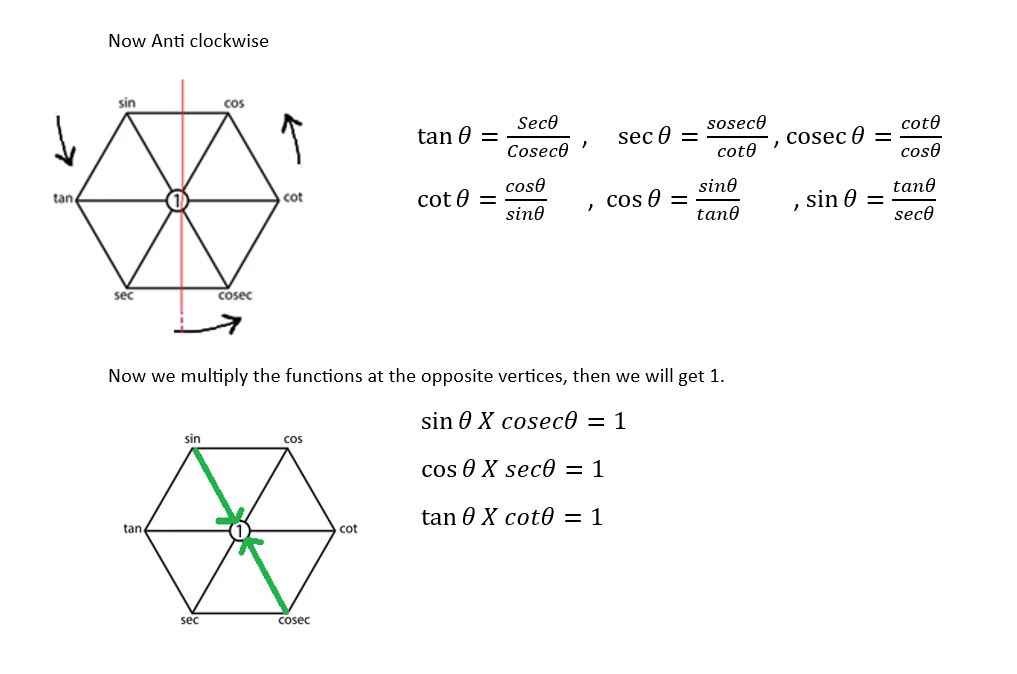
Now we take any three continuing functions in the hexagon like
tan
\tan
tan,
sin
\sin
sin, and
cos
\cos
cos. If the product of the first and the third functions results in the function between them.
现在我们取六边形中的任意三个连续函数,如
tan
\tan
tan、
sin
\sin
sin 和
cos
\cos
cos。如果第一个和第三个函数的乘积结果为它们之间的函数。
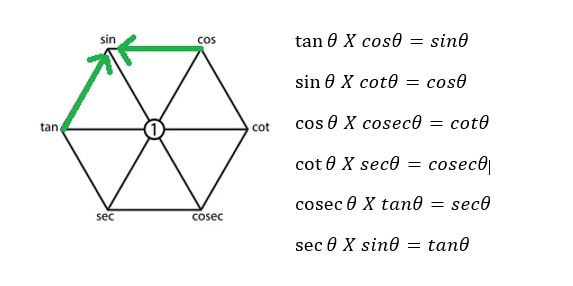
Now focus on the function diagonally opposite vertices. They are reciprocal of each other.
现在关注对角顶点的函数。它们互为倒数。
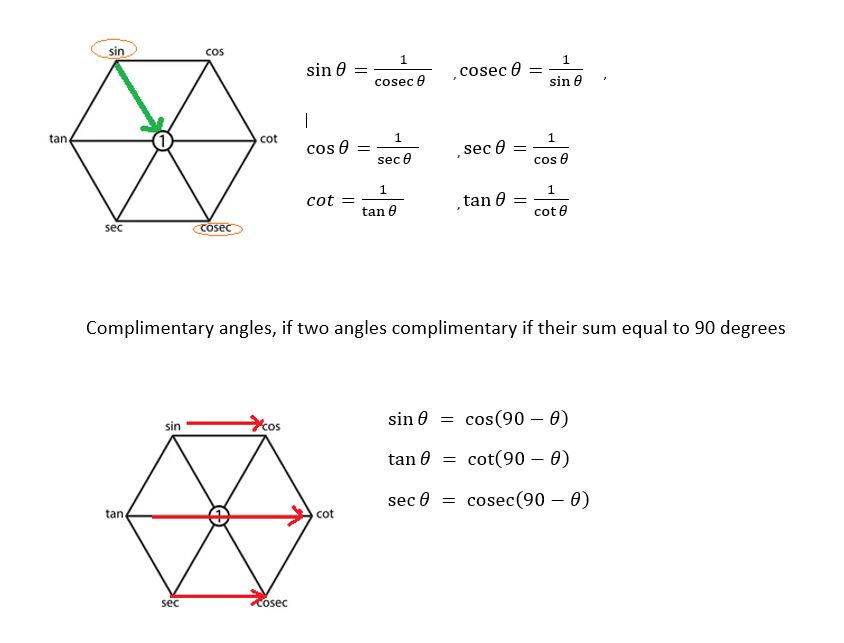
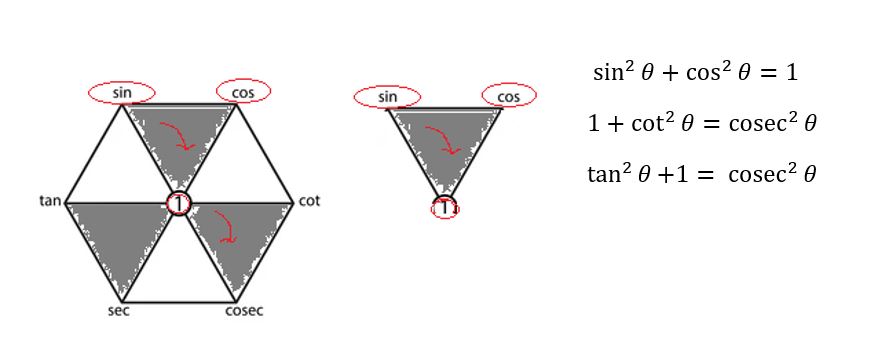
Focus the hexagon we found the six triangles. Focus only three triangle which s shadow in the image. Here we go clockwise within each one of the triangles starting with top left position. Square of the sum top two point of the triangle is equal to square off the bottom point of the triangle.
关注六边形,我们发现了六个三角形。只关注图像中阴影的三个三角形。在这里,我们从左上角位置开始,在每个三角形内顺时针进行。三角形顶部两个点的和的平方等于三角形底部点的平方。
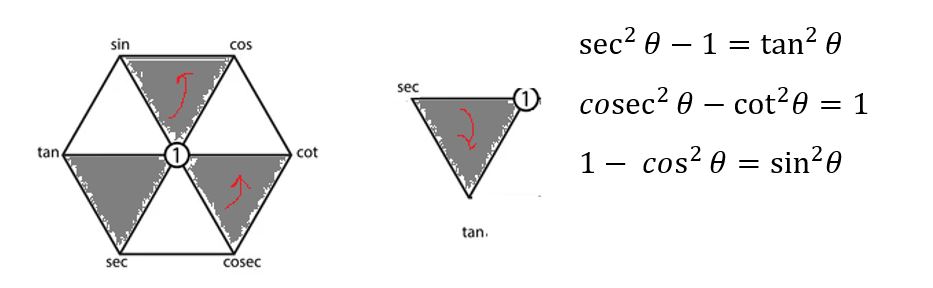
Anti-clock wise
Here we go anti-clockwise within each one of the triangles starting with top left position. Square of the subtraction top two point of the triangle is equal to square off the bottom point of the triangle
逆时针方向
在这里,我们从左上角位置开始,在每个三角形内逆时针进行。三角形顶部两个点的差的平方等于三角形底部点的平方
“counter-clockwise” 和 “anti-clockwise” 都有“逆时针”的意思,但存在一些区别:
counter-clockwise:“counter -” 前缀表示“反对、相反” ,强调与顺时针方向相反 ,更侧重于描述一种方向上的反向性。
美式英语中常用的表达 。比如在描述机械部件的转动方向、物体的旋转方向等场景中经常使用 。例如:“The fan rotates counter - clockwise.(风扇逆时针旋转。 )”anti-clockwise:“anti -” 前缀表示“反对、对抗、防止” ,表示与时钟转动方向相反 ,语义上更强调与常规顺时针方向的对抗。
英式英语中常用的表达。在英国及一些英联邦国家的日常生活、学术、工程等领域描述逆时针方向时较为常用 。例如:“Turn the knob anti - clockwise to reduce the volume.(逆时针转动旋钮来减小音量。 )”
via:
-
诱导公式_辞典百科
http://www.360doc.com/content/10/0826/12/2879493_48897160.shtml -
高中三角函数公式推理、记忆 - 知乎
https://zhuanlan.zhihu.com/p/106923495 -
三角函数公式六边形记忆法 - 知乎
https://zhuanlan.zhihu.com/p/354772973 -
用魔法六边形巧记三角恒等式 - 知乎
https://zhuanlan.zhihu.com/p/625979710
— -
從上述的定義 - 三角函数之間的關係
https://web.ntnu.edu.tw/~495403073/T3073_3061_1075/T2.htm -
第二章 基本三角函數 第 2 節 三角函數的基本關係
http://www.kut.com.tw/testfile/CABBM940200.pdf -
【数学】同角三角函数的基本关系–六边形记忆法_哔哩哔哩_bilibili
https://www.bilibili.com/video/BV1q7411J7i2/ -
Super magic Hexagon for Trigonometric identities Tricks – C3STREAM Land Designs
https://www.auraauro.com/uncategorized/super-magic-hexagon-for-trigonometric-identities-tricks/ -
Trigonometry Formulas for Functions, Ratios and Identities PDF
https://www.learncbse.in/trigonometry-formulas/

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








