几何学 | 从欧几里得到现代理论的多维探究-CSDN博客

本文链接：https://blog.csdn.net/u013669912/article/details/148031531

注：本文为“几何学”相关文章合辑。

英文引文，机翻未校。
中文引文，新增小标题。

略作重排，未全整理。

History of Geometry: Timeline of Discoveries, and Famous Geometers

几何学的历史：发现的时间线以及著名几何学家

Learn about the fascinating history of geometry, from its first known application in ancient civilizations to its relevance in current science and technology.
了解几何学从古代文明中的首次应用到现代科学和技术中的重要性的迷人历史。

By Hrothsige Frithowulf
Published: September 4, 2022

History of geometry

Mandelbrot set. (Public Domain)
曼德勃罗集合。

What is the history of geometry? The term “geometry” is derived from the ancient Greek word “geometria,” which means measurement (-metria) of earth or land (geo), but this branch of mathematics covers much more than mapping. Geometry explains the relationship between shape and size, and also the nature of mathematics and numbers. Find out more about the invention and history of geometry, as well as the pioneers of geometry and the groundbreaking discoveries they made that have shaped the field.
几何学的历史 是怎样的？“几何学”一词源自古希腊语“geometria”，意思是测量（-metria）地球或土地（geo），但这一数学分支涵盖的内容远不止制图。几何学解释了形状与大小之间的关系，以及数学和数字的本质。了解更多关于几何学的发明和历史，以及几何学先驱们所做的开创性发现，这些发现塑造了这一领域。

Discovery and Origin of Geometry

几何学的发现与起源

Ancient civilizations in places like the Indus Valley and Babylonia roughly 3000 BC are credited with laying the groundwork for geometry. Geometry first appeared in the ancient world as a set of rules and formulas suitable for planning, constructing, astronomy, and solving mathematical problems. These principles included length, area, angle, and volume. Cubic and spherical Indus weights and measures were crafted from chert, jasper, and agate.
大约在 公元前 3000 年 ，印度河流域和美索不达米亚的古老文明为几何学奠定了基础。几何学最初以一套适用于规划、建筑、天文学和解决数学问题的规则和公式的形式出现在古代世界。这些原理包括长度、面积、角度和体积。印度河流域的立方体和球形砝码及度量衡工具是由燧石、玉髓和玛瑙制成的。

Beginning around the 6th century BC, the Greeks expanded this knowledge and, using it, developed the conceptual field currently recognized as “geometry.” Greek philosophers such as Thales (624-545 BC), Pythagoras (570-490 BC), and Plato (428-347 BC) realized the fundamental relationship between the nature of space and geometry and reinforced geometry as an important field of study belonging to mathematics.
大约在公元前 6 世纪，希腊人扩展了这些知识，并在此基础上发展出了目前公认的“几何学”概念领域。希腊哲学家泰勒斯（公元前 624-545 年）、毕达哥拉斯（公元前 570-490 年）和柏拉图（公元前 428-347 年）认识到空间的本质与几何学之间的基本关系，并进一步巩固了几何学作为数学的一个重要研究领域。

Euclid (325-265 BC), who was probably Plato’s student and worked as a teacher in Alexandria, summed up the early Greek geometry in his magnificent work, “Elements,” written in 300 BC, and created scientific principles for geometric models using a handful of simple rules and axioms. The Elements became a standard geometry textbook for over 2000 years.
欧几里得（公元前 325-265 年）可能是柏拉图的学生，并在亚历山大港担任教师，他在公元前 300 年撰写的杰作《几何原本》总结了早期希腊几何学，并利用一些简单的规则和公理为几何模型创立了科学原理。《几何原本》成为 2000 多年来标准的几何学教科书。

Let no one ignorant of geometry enter.
Plato, Greek philosopher, and mathematician

不懂几何学者不得入内。

柏拉图，希腊哲学家和数学家

The Turning Point in the History of Geometry

几何学历史的转折点

Throughout the Middle Ages, mathematicians and philosophers from different cultures continued to use geometry to create a model of the universe. But the next major milestone came with the work of the French mathematician and philosopher René Descartes (1596-1650), who lived in the 17th century. Descartes developed coordinate systems to define the positions of the points in two-dimensional and three-dimensional space led to the birth of the field of analytical geometry, a new tool of mathematical algebra to solve and define geometry problems.
在整个中世纪，来自不同文化的数学家和哲学家继续利用几何学构建宇宙模型。然而，下一个重大里程碑是 17 世纪法国数学家和哲学家 勒内·笛卡尔（1596-1650）的工作。笛卡尔开发了坐标系统，用于定义二维和三维空间中点的位置，从而诞生了 解析几何 领域，这是一种新的数学代数工具，用于解决和定义几何问题。

Descartes’ work also led to the emergence of far more exotic forms of geometry. Mathematicians had long known that there were regions, such as the surface of a sphere, where the axioms of Euclidean geometry did not apply. The discovery of non-Euclidean geometry helped clarify many more fundamental principles that combined numbers and geometry. In 1899, German mathematician David Hilbert (1862-1943) developed new and more generalized axioms. Throughout the 20th and 21st centuries, these axioms were applied to a wide variety of mathematical cases.
笛卡尔的工作还促使了更具异国情调的几何形式的出现。长期以来，数学家们一直知道有一些区域，例如球体的表面，欧几里得几何的公理并不适用。非欧几里得几何 的发现有助于阐明更多结合数字和几何的基本原理。1899 年，德国数学家 大卫·希尔伯特（1862-1943）发展了新的、更一般的公理。在 20 世纪和 21 世纪，这些公理被应用于各种数学案例。

Timeline of the History of Geometry

几何学发展的时间脉络

The timeline of geometry begins with the birth of practical geometry and concludes with fractal geometry.
几何学的时间线始于实用几何学的诞生，并以分形几何学结束。

3000 BC – Practical Geometry

公元前 3000 年 – 实用几何学

实用几何学是几何学历史的开端。图片：吉萨金字塔。

The history of geometry first arose in the Indus Valley and Babylonian civilizations from the need to solve problems such as calculating the volume of material required to build a pyramid. The level of sophistication of some of these early concepts is so high that a contemporary mathematician can struggle to deduce them without resorting to calculus.
几何学的历史最初起源于印度河流域和美索不达米亚文明，源于解决诸如计算建造金字塔所需材料体积等问题的需要。这些早期概念的复杂程度如此之高，以至于现代数学家如果不借助微积分，可能会难以推导出它们。

300 BC – Spherical Geometry

公元前 300 年 – 球面几何学

Ptolemy was one of the pioneers of the geometry

Ptolemy with armillary sphere model, 1476. (Public Domain)
托勒密与天球仪模型，1476 年。

The Greek astronomer Theodosius of Bithynia (169-100 BC) compiled “spherics” in a book that consolidated the earlier work by Euclid (325-265 BC) and Autolycus of Pitane (360-290 BC) on spherical astronomy. In his Elements book, which was regarded as authoritative all the way up to the early 19th century in the history of geometry, Euclid provided the foundation for geometry.
希腊天文学家比提尼亚的狄奥多修斯（公元前 169-100 年）编撰了一本关于“球面学”的书，总结了欧几里得（公元前 325-265 年）和皮提亚的奥托吕科斯（公元前 360-290 年）在球面天文学方面的早期工作。在他的《几何原本》一书中，欧几里得为几何学奠定了基础，这本书在几何学的历史上一直被视为权威，直到 19 世纪初。

The spherical geometry allowed calculating areas and angles on spherical surfaces, such as star or planet positions in the imaginary sky sphere used by astronomers, or the locations of points on a map. However, this system does not follow Euclidean rules. In spherical geometry, the sum of a triangle’s angles is more than 180 degrees, and lines that run parallel to each other eventually meet. Euclid is considered the “father of geometry.”
球面几何学允许计算球面上的面积和角度，例如天文学家使用的假想天球上的恒星或行星位置，或者地图上点的位置。然而，这一系统并不遵循欧几里得规则。在球面几何学中，三角形的内角和大于 180 度，平行线最终会相交。欧几里得被认为是“几何学之父”。

500 BC – Pythagoras

公元前 500 年 – 毕达哥拉斯

Pythagoras was one of the pioneers of the geometry

Pythagoras. (Public Domain)
毕达哥拉斯。

The Greek philosopher named the “Pythagoras theorem”, which calculates the hypotenuse (the longest side) of a right-angled triangle from the lengths of the other edges. The theory that a triangle’s angles would sum to 180 degrees, or two right angles, is attributed to Pythagoras of Samos.
希腊哲学家命名了“毕达哥拉斯定理”，该定理可以根据直角三角形的其他两边长度计算斜边（最长边）的长度。三角形内角和为 180 度（或两个直角）的理论被归功于萨摩斯的毕达哥拉斯。

He said that the sum of the squares of the other two sides of a right triangle equals the square of the hypotenuse (the side opposite the right angle). Whenever the ancient engineers knew the lengths of two sides of a right triangle and needed to figure out the third, they used this theorem to do so, just like we do today.
他指出，直角三角形的另外两边的平方和等于斜边（直角的对边）的平方。每当古代工程师知道直角三角形的两边长度并需要计算第三边时，他们就会使用这个定理，就像我们今天所做的那样。

The idea of similar triangles, whereby two triangles are similar if they have the same form but need not have the same size, was also created by Pythagoras (570-490 BC). Pythagoras is remembered as a pivotal figure in the development of geometry.
相似三角形的概念也是由毕达哥拉斯（公元前 570-490 年）提出的，即如果两个三角形形状相同但大小不必相同，则它们是相似的。毕达哥拉斯被认为是几何学发展中的关键人物。

4th Century BC – Geometric Tools

公元前 4 世纪 – 几何工具

One of the first geometry tools. Women teaching geometry.

One of the first geometry tools. Woman teaching geometry.
最早的几何工具之一。教授几何学的女性。

Since the geometric tools have been around for thousands of years in the history of geometry, their precise historical beginnings are difficult to ascertain. However, the use of geometric instruments to measure, sketch, and build geometric forms and constructions may be traced back to at least the ancient Egyptians and Greeks. The Egyptians employed geometric tools in the building of their pyramids. The Greeks founded the science of geometry and wrote extensively on the use of geometric tools. They have undergone significant changes throughout the time.
由于几何工具在几何学的历史中已经存在了数千年，其确切的历史起源很难确定。然而，使用几何仪器进行测量、绘图和构建几何形状及构造的历史可以追溯到至少古埃及人和希腊人。埃及人在建造金字塔时使用了几何工具。希腊人创立了几何学，并广泛撰写了关于几何工具使用的文章。这些工具在不同时期经历了重大变化。

The Greek philosopher Plato (428-347 BC) stated that the tools of a true geometer should be limited to a straightedge and a compass, thereby establishing geometry as a science rather than a practical mastery. Euclid (325-265 BC), the “father of geometry,” and subsequent geometers defined the method of creating geometrical forms using certain tools. The ancient Greeks were the first to present building challenges using just a straightedge and compass. Some examples are building a line that is twice as long as another line or a line that divides an angle into two equal halves.
希腊哲学家柏拉图（公元前 428-347 年）指出，真正的几何学家的工具应仅限于直尺和圆规，从而将几何学确立为一门科学，而不仅仅是一种实用技艺。欧几里得（公元前 325-265 年），被称为“几何学之父”，以及后来的几何学家，定义了使用特定工具创建几何形状的方法。古希腊人是最早仅使用直尺和圆规进行构建挑战的人。例如，构建一条长度是另一条线段两倍的线段，或者将一个角平分成两个相等的角。

360 BC – Platonic Solids

公元前 360 年 – 柏拉图立体

在这里插入图片描述

Plato introduced the concept of the Platonic solids first in his dialogue “Timaeus.” The Platonic solids are known as the five regular convex polyhedra (polygonal bodies), but Plato also combined them with his ideas about the structure of matter in 360 BC. The Platonic solids include five shapes that can be formed by joining similar faces along the edges. The tetrahedron has four faces, the cube has six, the octahedron has eight, the dodecahedron has twelve, and the icosahedron has twenty faces.
柏拉图在其对话录《蒂迈欧篇》中首次引入了柏拉图立体的概念。柏拉图立体被称为五种正多面体（多边形体），但柏拉图还在公元前 360 年将它们与他对物质结构的想法结合起来。柏拉图立体包括五种可以通过沿边连接相似面形成的形状。四面体有四个面，立方体有六个面，八面体有八个面，十二面体有十二个面，二十面体有二十个面。

In this “Timaeus,” Plato equated the five Platonic solids with the classical elements (earth, air, fire, and water) and the fifth element of the universe, which he named the “quintessence.”
在《蒂迈欧篇》中，柏拉图将五种柏拉图立体与古典元素（土、气、火、水）以及他所命名的宇宙第五元素“精粹”联系起来。

In the history of geometry, mathematicians and philosophers have always had a healthy respect for and fascination with the Platonic solids. They have also found applications in the fields of art, design, and architecture, and have served as inspiration for the development of several additional three-dimensional forms. The Platonic solids are still widely studied and admired for their symmetry and elegance, making them an integral element of modern geometry.
在几何学的历史中，数学家和哲学家一直对柏拉图立体保持着健康的尊重和浓厚的兴趣。它们还在艺术、设计和建筑领域找到了应用，并激发了多种其他三维形式的发展。柏拉图立体因其对称性和优雅性而被广泛研究和赞赏，成为现代几何学的一个重要组成部分。

240 BC – Archimedean Solids

公元前 240 年 – 阿基米德立体

All the edges of the Archimedean solids.

All the edges of the Archimedean solids. (Photo, fdecomite, CC BY 2.0)
阿基米德立体的所有边。（照片，fdecomite，CC BY 2.0 许可）

The Greek mathematician Pappus of Alexandria (who flourished in 320 AD) described 13 convex polyhedrons, which are uniform polygons with similar edges and corners. In all, there are 14 Archimedean solids, 13 of which are attributed to Archimedes. In his 240 BC book, “Measurement of a Circle,” he detailed his study on these solids. The value of pi was approximated in this book by the Greek mathematician using the Archimedean solids.
希腊数学家亚历山大的帕普斯（公元 320 年活跃）描述了 13 种凸多面体，它们是具有相似边和角的均匀多边形。总共有 14 种阿基米德立体，其中 13 种被归功于阿基米德。在他的公元前 240 年的著作《圆的度量》中，他详细研究了这些立体。希腊数学家在这本书中利用阿基米德立体近似计算了圆周率的值。

Archimedean solids are a class of polyhedra. To qualify as one of these solids, each of the faces of an object must be a congruent regular polygon, and there must be vertices at which two or more polygons intersect. Archimedean solids differ from Platonic solids in that their vertices do not always have the same number of faces meeting.
阿基米德立体是一类多面体。要成为这类立体，物体的每个面都必须是全等的正多边形，并且必须有顶点是两个或多个多边形的交点。阿基米德立体与柏拉图立体的不同之处在于，它们的顶点并不总是由相同数量的面相交而成。

9th Century – Islamic Geometry

9 世纪 – 伊斯兰几何学

Geometric Tiles, Mosque of Moulay Idriss, Morocco. (Photo, Dimitry B. CC BY)
几何瓷砖，摩洛哥穆莱伊德里斯清真寺。（照片，Dimitry B. CC BY）

Mathematicians and astronomers of the Islamic world explored the possibilities of spherical geometry. The geometric models used in Islamic decoration during this period are similar to modern fractal geometry.
伊斯兰世界的数学家和天文学家探索了球面几何学的可能性。这一时期用于伊斯兰装饰的几何模型与现代分形几何学相似。

Geometric principles and the recurrence of geometric patterns are central to Islamic geometry, which is known for its ornate and aesthetically pleasing forms. Stars, polygons, and both regular and irregular tessellations are common components of these patterns.
几何原理和几何图案的重复是伊斯兰几何学的核心，它以其华丽且美观的形式而闻名。星星、多边形以及规则和不规则的镶嵌图案是这些图案的常见组成部分。

During the Islamic Golden Age (about the 8th to 13th centuries), Islamic geometry emerged as its own culture. Structures, tiles, textiles, and other ornamental arts all made use of these patterns and designs.
在伊斯兰黄金时代（大约 8 世纪到 13 世纪），伊斯兰几何学形成了自己的文化。建筑、瓷砖、纺织品和其他装饰艺术都使用了这些图案和设计。

1619 – Kepler’s Polyhedron

1619 年 – 开普勒多面体

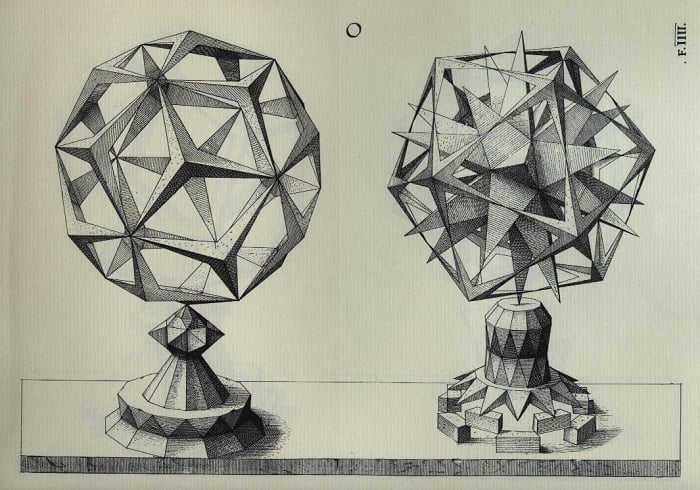
Kepler's 1619 polyhedra

Kepler’s Polyhedron: Octahedron and hedgehog in a cage. (Image)

German mathematician Johannes Kepler (1571-1630) discovered a new class of polyhedra, known as the star polyhedron. In his 1619 treatise “Harmonices Mundi,” Kepler described a set of four polyhedra. These “Kepler-Poinsot polyhedra” are the small stellated dodecahedron, the great stellated dodecahedron, the great dodecahedron, and the great icosahedron.
德国数学家约翰内斯·开普勒（1571-1630）发现了一类新的多面体，称为星形多面体。在他的 1619 年著作《世界的和谐》中，开普勒描述了四种多面体。这些“开普勒-泊松多面体”分别是小星形十二面体、大星形十二面体、大十二面体和大二十面体。

The Platonic and Archimedean solids, which are likewise polyhedra but have regular polygons for faces, are closely linked to Kepler’s polyhedra. Kepler’s polyhedra differ from these solids in that not all of their vertices are shared by the same number of faces. In Kepler’s mind, these geometric patterns reflected the underlying structure of the cosmos and hence had a cosmic meaning.
柏拉图立体和阿基米德立体也是多面体，但它们的面是正多边形，与开普勒多面体密切相关。开普勒多面体与这些立体的不同之处在于，并非所有顶点都由相同数量的面共享。在开普勒看来，这些几何图案反映了宇宙的底层结构，因此具有宇宙学意义。

1637 – Analytical Geometry

1637 年 – 解析几何学

1637 marked the analytical geometry

“La Geométrie,” a fascinating book by the French mathematician and philosopher René Descartes, explains how points in space can be measured by coordinate systems and geometric structures can be described by equations. This is called “analytical geometry,” and it is a field of study.
法国数学家和哲学家勒内·笛卡尔的著作《几何学》解释了如何通过坐标系统测量空间中的点以及如何用方程描述几何结构。这被称为“解析几何学”，是一门学科。

The study of geometric forms and their attributes is the domain of analytical geometry, often referred to as coordinate geometry or Cartesian geometry. Many consider René Descartes to be the “father” of analytical geometry because of his work in this area.
解析几何学，通常也称为坐标几何学或笛卡尔几何学，研究几何形状及其属性。许多人因为笛卡尔在这一领域的贡献而称他为“解析几何学之父”。

Prior to the advent of analytical geometry, the measurement and qualities of physical objects and forms were at the center of the geometry field. Descartes’ ideas made possible the abstract analysis and description of geometric forms and their attributes using algebraic techniques.
在解析几何学出现之前，几何学主要关注物理对象和形状的测量和属性。笛卡尔的思想使得人们能够使用代数技术对几何形状及其属性进行抽象分析和描述。

In addition, he proposed the use of equations to define geometric forms and curves, which allowed for a more accurate and rigorous investigation of these objects and their attributes. Today, many disciplines rely on the tools and techniques developed in analytical geometry, making it an indispensable branch of mathematics in the history of geometry.
此外，他还提出使用方程定义几何形状和曲线，这使得对这些对象及其属性的研究更加准确和严谨。如今，许多学科依赖于解析几何学中发展的工具和技术，使其成为几何学历史上不可或缺的数学分支。

1858 – Topology

1858 年 – 拓扑学

Topology began in 1858 in the history of geometry.
拓扑学在几何学的历史中始于 1858 年。

Möbius strip. (David Benbennick • CC BY-SA 3.0)
莫比乌斯带。（David Benbennick • CC BY-SA 3.0 许可）

During the 19th century, mathematicians began to be fascinated by topology, or geometric edges and surfaces rather than specific shapes. The visualized Möbius strip above is an object with a single surface and a single continuous edge.
在 19 世纪，数学家开始对拓扑学产生兴趣，拓扑学关注几何图形的边缘和表面，而不是具体的形状。上面的莫比乌斯带是一个具有单一表面和单一连续边缘的物体。

Topology is the mathematical study of the features of geometrical objects and spaces that remain unchanged while they are continuously deformed. It can be deformed by stretching, bending, and twisting, but not by ripping or gluing.
拓扑学是数学中研究几何对象和空间在连续变形过程中保持不变的特征的学科。它可以通过拉伸、弯曲和扭曲进行变形，但不能通过撕裂或粘合来变形。

Leonard Euler, a Swiss mathematician who flourished in the 18th century, is considered the father of modern topology. Using what would become known as graph theory, Euler investigated the topology of polyhedra. Graph theory is the study of networks made up of points and lines.
18 世纪活跃的瑞士数学家莱昂哈德·欧拉被认为是现代拓扑学之父。他利用后来被称为图论的方法研究了多面体的拓扑学。图论是研究由点和线构成的网络的学科。

The notion of the Möbius strip, a surface with just one side and one border, was established by August Ferdinand Möbius and Johann Benedict Listing, who contributed to the advancement of topology in the 19th century. To explore various mathematical objects and structures such as manifolds, knots, and topological spaces, topology evolved into a more abstract and generic discipline in the 20th century.
莫比乌斯带的概念——一个只有一面和一个边界的表面——由奥古斯特·费迪南德·莫比乌斯和约翰·贝内迪克特·利斯廷确立，他们为 19 世纪拓扑学的发展做出了贡献。为了探索流形、纽结和拓扑空间等各种数学对象和结构，拓扑学在 20 世纪发展成为一个更加抽象和通用的学科。

1882 – The Discovery of the Klein Bottle

1882 年 – 克莱因瓶的发现

This geometric Klein bottle was invented in 1882

Klein Bottle. (Image: Dzen.ru)
克莱因瓶。（图片：Dzen.ru）

German scientist Felix Klein (1849-1925) discovered a shape that has a one-sided surface without any surface borders, which proves to be a geometry with more than three dimensions. Felix Klein initially characterized it in the 19th century as a tool for investigating the characteristics of non-orientable surfaces.
德国科学家费利克斯·克莱因（1849-1925）发现了一种具有一侧表面且没有边界的一维几何形状，这被证明是一种超过三维的几何结构。费利克斯·克莱因在 19 世纪最初将其描述为一种用于研究不可定向表面特征的工具。

The Klein bottle is not characterized by its geometric form but rather by its attributes and connections to other things, making it a topological entity. It is a mathematical description of a surface with no obvious boundaries, and it may be thought of as a loop that has been twisted and linked to itself.
克莱因瓶不是以其几何形状为特征，而是以其属性和与其他事物的联系为特征，使其成为一种拓扑实体。它是一种没有明显边界的表面的数学描述，可以被看作是一个被扭曲并连接到自身的环。

One of the fascinating features of the Klein bottle is that it can’t be immersed in three-dimensional space without crossing over into itself. Because of this feature, the Klein bottle is notoriously hard to draw to scale, prompting the creation of a number of computer techniques for studying and understanding its features.
克莱因瓶的一个有趣特点是，它不能在三维空间中浸入而不与自身相交。由于这一特点，克莱因瓶很难按比例绘制，这促使人们开发了许多计算机技术来研究和理解其特征。

20th Century – Fractal Geometry

20 世纪 – 分形几何学

$20th century marked the fractal geometry. This is a mandelbrot set.$

The fractal geometry is a turning point in the history of geometry. (Photo, Wolfgang Beyer, CC BY-SA 3.0)
分形几何学是几何学历史上的一个转折点。（照片，Wolfgang Beyer，CC BY-SA 3.0 许可）

Our ability to use computers has led to the discovery of fractals, which are equations of detailed models that repeat each other at different scales and produce shapes like the well-known Mandelbrot set and display them in a graphical form.
我们使用计算机的能力促使了分形的发现，分形是在不同尺度上相互重复的详细模型的方程，并产生像著名的曼德勃罗集合这样的形状，并以图形形式显示它们。

Mathematically speaking, fractal geometry is the study of the characteristics of geometric objects with both self-similarity and a non-integer dimension. Many definitions of fractals focus on the fact that they are geometric forms with “fractional dimension,” or a dimension that is between a whole number and a fraction.
从数学上讲，分形几何学研究具有自相似性和非整数维度的几何对象的特征。许多分形的定义都集中在它们是具有“分数维度”的几何形状，即介于整数和分数之间的维度。

The French mathematician Henri Poincaré used the word “fractal” to characterize things having a “fractional dimension” in the early 20th century. However, the German mathematician Georg Cantor researched the idea of self-similarity, a central aspect of fractals, far earlier, in the 19th century.
20 世纪初，法国数学家亨利·庞加莱用“分形”一词来描述具有“分数维度”的事物。然而，德国数学家格奥尔格·康托尔早在 19 世纪就研究了自相似性的概念，这是分形的核心特征。

Benoit Mandelbrot, a mathematician born in Poland, is widely recognized as the pioneer of fractal geometry. He made significant contributions to the area in the 1970s. Mandelbrot used the term “fractal geometry” to characterize the emerging area of study he established by using computer graphics to show and analyze the characteristics of fractals.
出生于波兰的数学家本华·曼德勃罗被广泛认为是分形几何学的先驱。他在 20 世纪 70 年代对该领域做出了重大贡献。曼德勃罗使用“分形几何学”一词来描述他通过计算机图形展示和分析分形特征而建立的新兴研究领域。

Fractal geometry has relevance in many modern disciplines, such as physics, biology, and computer science. It’s also used in the development of computer graphics as well as the research of chaotic systems.
分形几何学在许多现代学科中都有应用，例如物理学、生物学和计算机科学。它还被用于计算机图形学的发展以及混沌系统的研究。

Today—Computational Geometry

当代 – 计算几何学

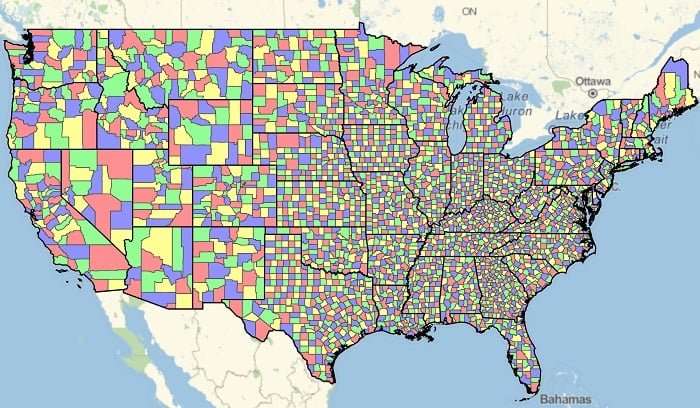
united states of america map in four-color theorem

(Image author: Greg Hurst)
（图片作者：Greg Hurst）

The computer’s power allowed us to solve problems such as the four-color theorem, which distinguishes the various regions within a complex map using nothing but four colors in such a way that no two adjacent regions on the map have the same color.
计算机的强大能力使我们能够解决诸如四色定理这样的问题，该定理仅使用四种颜色来区分复杂地图中的各个区域，使得地图上没有两个相邻区域具有相同的颜色。

Francis Guthrie introduced the four-color theorem in 1852, then in 1976, Kenneth Appel and Wolfgang Haken used computer systems to verify it. Extensive computer computations were used to prove the four-color theorem, which states that every map can be colored using just four colors.
弗朗西斯·古斯里在 1852 年提出了四色定理，然后在 1976 年，肯尼斯·阿佩尔和沃尔夫冈·哈肯使用计算机系统验证了它。大量的计算机计算被用来证明四色定理，该定理指出每张地图都可以仅用四种颜色进行着色。

Useful in many disciplines, including cartography and computer science, the four-color theorem is worth studying. It’s used to make comprehensible maps, and it’s spawned new computational and mathematical methods for investigating and comprehending the characteristics of maps and other spatial systems.
四色定理在许多学科中都有应用，包括制图学和计算机科学，值得研究。它用于制作易于理解的地图，并催生了用于研究和理解地图及其他空间系统特征的新计算和数学方法。

Types of Geometry

几何学的类型

Euclidean Geometry

欧几里得几何学

Euclidean geometry is analyzing shapes in two dimensions and three dimensions according to the rules established by Euclid, an ancient Greek mathematician. One defining feature of Euclidean geometry is that its definitions and theorems are grounded in axioms, or universally accepted facts.
欧几里得几何学 是根据古希腊数学家欧几里得所确立的规则，分析二维和三维空间中的形状。欧几里得几何学的一个定义特征是，其定义和定理都基于公理，即被普遍接受的事实。

Euclidean geometry, named after the ancient Greek mathematician who developed it, is one of the most widespread kinds of geometry. Axioms, or fundamental principles, form the foundation of Euclidean geometry. For example, it is an axiom that any two straight lines will meet at a single point. This branch of geometry is very applicable since it explains the behavior of solid forms and objects in the physical world.
以创立该学科的古希腊数学家命名的欧几里得几何学是最为广泛的一种几何学。公理，即基本原理，构成了欧几里得几何学的基础。例如，一个公理是任意两条直线将在一个点上相交。这一几何学分支具有很强的实用性，因为它解释了物理世界中实体形状和物体的行为。

Non-Euclidean Geometry

非欧几里得几何学

This branch of geometry is distinguished from Euclidean geometry by its use of various axioms. Two examples of non-Euclidean geometries are hyperbolic geometry, which uses a different set of axioms for parallel lines, and elliptic geometry, which uses a different set of axioms for the sum of the angles in a triangle.
这一几何学分支因其使用不同的公理而与欧几里得几何学区别开来。非欧几里得几何学 的两个例子是：双曲几何学，它使用不同的公理来处理平行线；椭圆几何学，它使用不同的公理来处理三角形内角和。

Some of the assumptions of Euclidean geometry are rejected in non-Euclidean geometry. Hyperbolic geometry, one of the most well-known types of non-Euclidean geometry, is predicated on the premise that two lines can meet in more than one place. This branch of geometry is often used in the investigation of cosmological structure and space-time characteristics.
非欧几里得几何学拒绝了欧几里得几何学的一些假设。双曲几何学，作为一种最为人熟知的非欧几里得几何学，基于两条线可以在多于一个的地方相交这一前提。这一几何学分支常用于研究宇宙结构和时空特性。

Projective geometry

射影几何学

The focus here is on geometric shapes and transformations that keep length-to-width ratios (the ratios of distances) the same. Perspective drawings and other forms of graphics can be analyzed using projective geometry.
这里的重点是保持长宽比（距离比）不变的几何形状和变换。透视绘图和其他形式的图形可以用射影几何学来分析。

Projective geometry is the study of the characteristics of figures and forms when they are projected onto a two-dimensional plane, making it the third type of geometry. Creating perspective and the appearance of depth on a two-dimensional surface is made possible using this form of geometry, making it useful in art, architecture, and photography.
射影几何学 是研究图形和形状在投影到二维平面上时的特征，是第三种几何学类型。这种几何学使得在二维表面上创造出透视感和深度感成为可能，因此它在艺术、建筑学和摄影学中很有用。

Topological Geometry

拓扑几何学

The fourth type of geometry is topological geometry, which investigates the features of geometric objects that remain the same under continuous deformations like stretching or bending. This geometry is often used in the investigation of sub-atomic structures and cosmological characteristics.
第四种几何学类型是 拓扑几何学，它研究在拉伸或弯曲等连续变形下保持不变的几何对象的特征。这种几何学常用于研究亚原子结构和宇宙学特征。

Preserved features of geometric forms during continuous deformations like stretching or bending are the focus of this field of research. Deformable forms have interesting qualities that can be investigated using topology.
在拉伸或弯曲等连续变形过程中保持不变的几何形状的特征是这一研究领域的重点。可变形的形状具有可以用拓扑学来研究的有趣特性。

Differential Geometry

微分几何学

Differential geometry is a calculus-based research field in geometry. Curves and surfaces in three dimensions can be analyzed with the help of differential geometry. Numerous branches of science and technology rely heavily on the concepts and methods of differential geometry, such as physics, engineering, and computing. It is used in the investigation of spatial phenomena and the properties of dynamic physical systems.
微分几何学是基于微积分的几何学研究领域。借助微分几何学可以分析三维空间中的曲线和曲面。许多科学和技术分支，如物理学、工程学和计算机科学，严重依赖微分几何学的概念和方法。它用于研究空间现象和动态物理系统的性质。

It is a tool used in physics to learn more about the nature of space-time and how particles and fields behave. Manifolds are high-dimensional spaces used to simulate physical processes and investigate their characteristics.
它是物理学中用来更多地了解时空本质以及粒子和场如何行为的工具。流形是用于模拟物理过程并研究其特征的高维空间。

This type of geometry has many applications in engineering, including the study of surface qualities and the design and analysis of complex systems like airplanes and cars. In computer science, it is used to study data structures and algorithms and what makes them work the way they do.
这种几何学在工程学中有许多应用，包括研究表面特性以及设计和分析像飞机和汽车这样的复杂系统。在计算机科学中，它用于研究数据结构和算法以及它们的工作原理。

Algebraic Geometry

代数几何学

In algebraic geometry, we apply algebraic concepts and methods to the study of geometry. This field of study focuses on the qualities of shapes whose characteristics can be expressed in terms of equations. This type of geometry studies Algebraic curves, Algebraic surfaces, Algebraic varieties, and also manifolds. These are curves, surfaces, objects, and high-dimensional spaces that can be defined using algebraic equations such as parabolas, planes, ellipsoids, lines, circles or the curvature of space-time.
在代数几何学中，我们应用代数概念和方法来研究几何学。这一研究领域关注可以用方程表达其特征的形状的品质。这种几何学研究代数曲线、代数曲面、代数簇以及流形。这些是可以用代数方程定义的曲线、曲面、物体和高维空间，例如抛物线、平面、椭球体、直线、圆或时空的曲率。

In general, geometry is a fascinating and intricate mathematical field with several practical applications. Geometry is essential to our knowledge of the world around us, whether we’re trying to figure out how the cosmos formed or conjure up some impressive optical illusions.
总的来说，几何学是一个具有许多实际应用的迷人而复杂的数学领域。无论我们是试图弄清楚宇宙是如何形成的，还是创造出一些令人印象深刻的光学幻觉，几何学对于我们了解周围的世界都是至关重要的。

什么是几何学？

陈省身数学大院 2024 年 12 月 19 日 18:02 北京

陈省身教授（左）与周光召教授（右）在交谈，图源：求是科技基金会官网。

陈省身｜演讲

开场致辞

今天授奖的仪式很隆重，听了许多人的演讲，我非常感动。有机会在此演讲，自己觉得非常之荣幸，也非常之高兴。我想从现在起，我们就像平常上课一样，不怎么严肃，随便一点。我带了一些材料，非常遗憾的是没法投影。不投影也可以，我没有什么准备。

几何学的定义与重要性

大家希望我讲一点几何学，题目是《什么是几何学》。我虽然搞了几十年的几何工作，但是很抱歉的一点是，当你们听完演讲后，不会得到很简单的答案，因为这是一门广泛而伟大的学问。在最近几千年来，几何学有非常重要的发展，跟许多其它的科学不但有关系、有作用，而且是基本的因素。

欧几里德与《几何原本》

讲到几何学，我们第一个想到的是欧几里德。除了基督教的《圣经》之外，欧几里德的《几何原本》在世界出版物中大概是销售最多的一本书了。这本书在中国有翻译，译者是徐光启与利玛窦。徐光启（1562~1633）是中国了不得的学问家，利玛窦（M.Ricci）是到中国来的意大利传教士。他们只翻译了六章，中文本是在 1607 年出版的。

我们现在通用的许多名词，例如并行线、三角形、圆周等这类名词，我想都是徐光启翻译的。当时没有把全书翻译完，差不多只翻译了半本，另外还有半本是李善兰和伟烈亚力翻译的。伟烈亚力（A.Wylie）是英国传教士。很高兴的是，李善兰是浙江海宁人。海宁是嘉兴府的一县，我是嘉兴人，所以我们是同乡（掌声）。对了，查济民先生也是海宁人（掌声）。

笛卡儿与坐标几何

推动几何学第二个重要的、历史性发展的人是 Descarte（1596~1650），中国人翻译称为笛卡儿。他是法国哲学家，不是专门研究数学的。他用坐标的方法，把几何变成了代数。当时没有分析或者无穷的观念，所以他就变成代数。我想笛卡儿当时不见得觉得他这贡献是很伟大的，所以他的几何论文是他的哲学引里面最后的一个附录，附属于他的哲学的。

这个思想当然在几何上是革命性的，因为当把几何的现象用坐标表示出来时，就变成了代数现象。所以你要证明说一条直线是不是经过一个点，你只要证明某个数是不是等于零就行了。这样就变成了一个简单一点的代数问题。当然并不是任何的几何问题都要变成代数问题，有时候变为代数问题后原来的问题更加复杂了。但这个关系是基本性的。

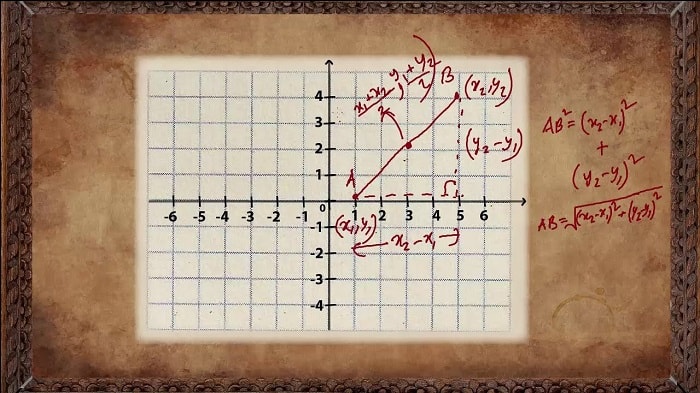
笛卡儿发现的坐标系，我们大概在中学念解析几何都学到。有一点是这样的（我的图可惜现在没法投影出来），给定一条直线，直线上有一个原点，其它的点由它的距离 $x$ 来确定，然后经过 $x$ 沿一定的方向画一条直线，那么 $y$ 坐标就是在那条线从 $x$ 轴上这个点所经的距离，这就是笛卡儿的坐标，英文叫 Cartesian 坐标。它的两条线不一定垂直。不知道哪位先生写教科书时把两条线写成垂直了，因此 $x$ 坐标与 $y$ 坐标对称了。笛卡儿的两个坐标不是对称的，这是他非常重要的观念，我们现在就叫纤维丛。

这些跟 $y$ 坐标平行的直线都是纤维，是另外的一个空间。原因是这样的：你把它这样改了之后，那条直线就不一定要直线，可以是任何另外一个空间了。这样可以确定空间里点用另外一组坐标来表示。所以有时候科学或数学不一定完全进步了，有时候反而退步了（笑声）。笛卡儿用了这个坐标，就发现，我们不一定要用 Cartesian 坐标，可以用其它坐标，比如极坐标。

平面上确定一个点，称为原点，过这点画一条射线，称为原轴。这样平面上的点，一个坐标是这点与原点的距离，另外一个是角度，是这点与原点的连线与原轴的相交的角度，这就是极坐标。因此极坐标的两个坐标，一个是正数或零，另外一个是从零到 $360$ 度的角度。

当然我们都知道，还可以有许多其它的坐标，只要用数就可以确定坐标。因此，后来大家弄多了的话，就对几何作出了另外一个革命性的贡献，就是说，坐标不一定要有意义。只要每级数能定义一个点，我们就把它叫坐标。从而几何性质就变成坐标的一个代数性质，或者说分析的性质。这样就把几何数量化了，几何就变成形式化的东西了。

坐标的意义与爱因斯坦的困惑

这个影响非常之大，当然这个影响也不大容易被接受，比如爱因斯坦。爱因斯坦发现他的相对论，特殊相对论是在 1908 年，而广义相对论是在 1915 年，前后差了 7 年。爱因斯坦说，为什么需要 7 年我才能从特殊相对论过渡到广义相对论呢？他说因为我觉得坐标都应该有几何或物理意义。爱因斯坦是一个对学问非常严谨的人，他觉得没有意义的坐标不大容易被接受，所以耽误了他很多年，他才不能不接受，就是因为空间的概念被推广了。

我忘掉了一段。我现在是讲书，讲书忘掉了补充一下是无所谓的，讲错了也不要紧（笑声）。同样我回头再讲一点欧几里德。那时的欧几里德的《几何原本》并不仅仅是几何，而是整个数学。因为那时候的数学还没有发现微积分，无穷的观念虽然已经有了，不过不怎么普遍。

我再说一点，就很可惜的是欧几里德的身世我们知道得很少，只知道他大概生活在纪元前三百年左右。他是亚历山大学校的几何教授，他的《几何原本》大概是当时的一个课本。亚历山大大学是希腊文化最后集中的一个地方。因为亚历山大自己到过亚历山大，因此就建立了当时北非的大城，靠在地中海。但是他远在到亚洲之后，我们知道他很快就死了。

之后，他的大将托勒密（Ptolemy Soter）管理当时的埃及区域。托勒密很重视学问，就成立了一个大学。这个大学就在他的王宫旁边，是当时全世界伟大的大学，设备非常好，有许多书。很可惜由于宗教的原因，由于众多的原因，现在这个学校被完全毁掉了。当时的基督教就不喜欢这个学校，已经开始被毁了，然后回教人占领了北非之后，就大规模地破坏，把图书馆的书都拿出来烧掉。所以现在这个学校完全不存在了。

几何学与数学的联系

几何是很重要的，因为大家觉得几何就是数学。比方说，现在还有这一印象，法国的科学院，它的数学组叫做几何组。对于法国来讲，搞数学的不称数学家，而叫几何学家，这都是受当时几何的影响。当时的几何比现在的几何的范围来得广。不过从另一方面讲现在的范围更广了，就是我刚才讲到的坐标不一定有意义。一个空间可以有好几种坐标，那么怎样描述空间呢？这就显得很困难啦，因为空间到底有什么样的几何性质，这也是一个大问题。

高斯与黎曼的贡献

高斯与黎曼建立和发展了这方面的理论。高斯是德国人，我想他是近代数学最伟大的一个数学家。黎曼实际上是他的继承人，也是德国数学家。他们都是哥廷根大学的教授。可惜的是黎曼活着时身体不好，有肺结核病，四十岁就死了。他们的发展有一个主要目的，就是要发展一个空间，它的坐标是局部的。空间里只有坐标，反正你不能讲坐标是什么，只知道坐标代表一个点，所以只是一小块里的点可以用坐标表示。因此虽然点的性质可以用解析关系来表示，但是如何研究空间这就成了大问题。

欧几里德的第五公设与非欧几何

在这个之前，我刚才又忘了一个，就是基础的数学是欧几里德的书，但是欧几里德的书出了一个毛病。因为欧几里德用公理经过逻辑的手段得到结论。例如说，三角形三角之和一定等于 $180$ 度，这是了不得的结果。欧几里德可以用公理几步就把它证明了，是一个结论。这个比现代的科学简单得多了。

我们刚才听了很多话，科学家做科学研究，第一样就是跟政府要钱，跟社会要钱，说你给了我钱，我才能做实验。当然实验是科学的基础。但是这样一来就会有许多的社会问题和政治问题。

欧几里德说，你给我一张纸，我只要写几下，就证明了这个结果。不但如此，我是搞数学的，我说数学理论还有优点，数学的理论可以预测实验的结果。不用实验，用数学可以得到结论，然后用实验去证明。当然实验有时的证明不对，也许你的理论就不对了，那当然也有这个毛病。

欧几里德的公理是非常明显的，但是他有一个有名的公理叫第五公设出了问题。这个第五公设讲起来比较长，但是简单地说，就是有一条直线与线外一点，经过这点只有一条直线与这条已给的直线平行。这个你要随便画图的话，觉得相当可信。可是你要严格追问的话，这个公理不大明显，至少不如其它公理这样明显。所以这个第五公设对当时数学界喜欢思想的人是个大问题。

当时最理想的情形是：第五公设可以用其它的公理推得，变成一个所谓的定理。那就简单化了，并且可做这个实验。我们搞数学的人有一个简单的方法，就是我要证明这个公理，我先假定这个公理不对，看是不是可以得到矛盾。如果得到矛盾，就证明它是对的了。这就是所谓间接证明法。有人就想用这个方法证明第五公设，但是都失败了。

我们现在知道这个第五公设并不一定对，经过一点的并行线可以有无数条，这就是非欧几何的发现。非欧几何的发现，它的社会意义很大，因为它表示空间不一定只有一个。西洋的社会相信上帝只有一个，怎么会有两个空间，或者很多个空间呢？当时这是个很严重的社会问题。

不止是社会问题，同时也是哲学问题。像德国大哲学家康德，他就觉得只能有欧氏几何，不能有非欧几何。所以当时这是一个很大的争论。非欧几何的发现一个是 J.Bolyai，匈牙利人，在 1832 年；一个是 Lobachevski，俄国人，在 1847 年。

不过我刚才讲到大数学家高斯，我们从他的种种著作中知道他完全清楚，但他没有把它发表成一个结论，因为发表这样一个结论，是可以遭到别人反对的。因此就有这么一个争论。等到意大利的几何学家 Beltrami，他在欧几里德的三维空间里造了一个曲面，曲面上的几何就是非欧几何，这对于消除大家的怀疑是很有利的工具。

因为上述结果是说，假定有一个三维的欧几里德空间，就可以造出一个非欧几何的空间来，所以在欧几里德的几何中亦有非欧几何。你假定欧几里德几何，你就得接受非欧几何，因此大家对非欧几何的怀疑有种种的方法慢慢给予解除。

拓扑学与黎曼几何

我刚才讲到高斯与黎曼把坐标一般化，使坐标不一定有意义，这对几何学产生的问题可大了。因为空间就变成一块一块拼起来的东西。那想怎么去研究它呢？怎么知道空间有不同的性质呢？甚至怎么区别不同的空间？

我这里有几个图，画了几个不同的空间，可惜我没法把它投影出来。不过，总而言之空间的个数是无穷的，有很多很多不同的空间。现在对于研究几何的人就产生一个基本问题，你怎样去研究它。这样一个基本的学问现在就叫 Topology，拓扑学。

它是研究整个空间的性质，如什么叫空间的连续性，怎样的两个空间在某个意义上是相同的，等等。这样就发展了许多许多的工具。这个问题也讨论了。黎曼生活在 1826~1866 年。德国的教学制度在博士毕业之后，为了有资格在大学教书，一定要做一个公开演讲，这个公开的演讲就是所谓的 Habilitationschrift。黎曼在 1854 年到哥廷根大学去做教授，做了一个演讲，这个在几何上是非常基本的文献。

如何研究这种空间呢？要研究这种空间，如果你只知道空间是随便一块块拼起来的话，就没有什么可以研究的了。于是你往往需要一个度量，至少你知道什么叫两点之间的距离，你怎么去处理它呢？就需要解析的工具。往往你把距离表为一个积分，用积分代表距离。

黎曼的这篇 1854 年的论文，是非常重要的，也是几何里的一个基本文献，相当一个国家的宪法似的。爱因斯坦不知道这篇论文，花了七年的时间想方设法也要发展同样的观念，所以爱因斯坦浪费了许多时间。黎曼这篇论文引进的距离这个观念，是一个积分，在数学界一百多年来有了很大的发展。

第一个重要的发展是黎曼几何应用到广义相对论，是相对论的一个基本的数学基础。现在大家要念数学，尤其要念几何学的话，黎曼几何是一个最主要的部分，这个也是从黎曼的演讲开始的。现在黎曼几何的结果多得不得了，不但是几何的基础，可能也是整个数学发展的基础。

我刚才提到一百多年来的发展。所谓的黎曼几何实际上是黎曼的论文的一个简单的情形，是某个情形。黎曼原来的意思，广义下的意思，有个人做了重要的工作，是一个德国人 Finsler。所以这部分的几何就叫 Finsler 几何。他在 1918 年在哥廷根大学写了一篇博士论文，就讲这个几何。这个几何后来发展不大多，因为大家不知道怎么办。如果这个度量的积分广了一点，对应的数学就变复杂了，不像黎曼的某个情形这样简单。

黎曼这情形也不简单。黎曼普通地就写了一个 $d s$ 的平方等于一个两次微分式，这个两次微分式积分一下就代表弧的长度。怎样研究这样的几何，这是需要一个像黎曼这种天才才有这个办法。黎曼就发展了他所谓的 Riemann curvature tensor，黎曼曲率张量。你若要搞这类几何的话，就要有张量的观念。而空间的弯曲性，这个弯曲性解析表示出来也比较复杂了，就是黎曼的曲率张量。

我们现在大家喜欢讲得奖。我们今天发奖，有奖金，要社会与政府对你的工作尊重。当年的时候你要搞数学的话，如果没有数学教授的位置，就没有人付你工资。一个主要的办法就是得奖金。有几个科学院它给奖金，得了奖金后你当然可以维持一段时间，因此就很高兴。不过很有意思的是我想 Riemann - Christoffel 曲率张量是一个很伟大的发现，黎曼就到法兰西科学院申请奖金。科学院的人看不懂，就没有给他。

所以诸位，今天坐在前排几位你们都是得奖人，都是得到光荣的人，我们对于你们寄予很大的期望，后面几排的大多数人没有得过奖，不过我安慰大家，没得过奖不要紧，没得过奖也可以做工作。我想我在得到学位之前，也没有得过奖。得不得到奖不是一个很重要的因素，黎曼就没有得到奖。他的 Riemann - Christoffel 张量在法兰西的科学院申请奖没有得到。

Finsler 几何的发展

最近虽然在黎曼几何上有很多发展，非常了不得的发展，但是大家对于一般的情形，黎曼论文的一般情形、Finsler 几何，没有做很多贡献。很巧的是我在 1942 年曾写了一篇 Finsler 几何的论文，就是找能把黎曼几何的结果做到 Finsler 几何的情形。

最近有两位年轻的中国人，一个叫鲍大维，一个叫沈忠民，我们合写了一本关于 Finsler 几何的书。这本书就要在 Springer - Verlag 出版，属于它的 Graduate Texts 数学丛书。编辑对于我们的书也很喜欢，给了我们一个很有意思的书号：200。书就在这里，我想这本书等会我会交给谷超豪教授，就把它放在复旦大学的某个图书馆里（掌声）。

我们这本书有一个小小的成就，就是把近一百年来最近在黎曼几何上的发现，我们把它推广到一般的情形，即黎曼 - Finsler 情形。这是黎曼当年的目的。黎曼当然非常伟大，不过他对于一般的情形不是很重视，他甚至在他的文章里讲这里没有新的东西，我们就把他说的没有新的东西做了一些出来。

物理与几何的关系

我知道我旁边坐了两位伟大的物理学家。接下去我想班门弄斧一下，谈一下物理与几何的关系。我觉得物理学里有很多重要的工作，是物理学家要证明说物理就是几何。

比方说，你从牛顿的第二运动定律开始。牛顿的第二定律说， $F = ma$ ， $F$ 是力， $m$ 是质量， $a$ 是加速度，加速度我们现在叫曲率。所以右边这一项是几何量，而力得当然是物理量。所以牛顿费了半天劲，他只是说物理就是几何（大笑，掌声）。不但如此，爱因斯坦的广义相对论也是这样。爱因斯坦的广义相对论的方程说：

$R_{ik} - \frac{1}{2} g_{ik} R = 8\pi K T_{ik}$

$R_{ik}$ 是 Ricci 曲率， $R$ 是 scalar curvature，即标量曲率， $K$ 是常数， $T_{ik}$ 是 energy - stress tensor，即能量 - 应力张量。你仔细想想，他的左边是几何量，是从黎曼度量得出来的一些曲率。所以爱因斯坦的重要方程式也就是说，几何量等于物理量（掌声）。

不止是这些，我们可以一直讲下去。我们现在研究的空间叫流形，是一块块空间拼起来的。这个流形不好研究。流形上的度量，你如果要把它能够用方程写下来的话，你一定要把流形线性化，一定要有一个所谓的向量空间，叫 vector space。

向量空间有一个好处，它的向量可以相加，可以相减，它还有种种不同的乘法。所以你就可以用解析的方法处理几何的情形。那么一般的流形怎么处理呢？数学家的办法很简单，就是在流形的每一点弄一个切平面。每一点都有个向量空间，叫切空间，跟它相切。

欧几里德空间只有一个切空间。现在的空间情况复杂了一些，每点都有一个切空间，但都是平坦空间。这个现象在几何上有一个重大的发展，就是把切空间竖起来。反正是一把向量空间，给流形的每点一个向量空间，不一定要是流形的切面或切空间。我们就叫它为纤维丛，或叫向量丛，向量空间丛。这个我想比爱因斯坦的（相对论）还要重要。Maxwell 方程就是建立在一个向量丛上。

你不是要一把向量空间吗？最好的是一把筷子，这里一维最好是复一维，complex。这把筷子每个都是复空间，它是骗人的一维，其实是二维，是复数空间。复数就有玩意儿了。现在是一把复数，你如果能有法子从这个纤维到另外一个纤维，有一个我们所谓的平行性的话，你就立刻得到 Maxwell 方程。

现代文明都靠电，控制电的方程的是 Maxwell 方程。现在纤维丛上有一个平行性，这个平行性的微分，等于电磁场的强度 $F$ ，然后你把这个 $F$ 再求它的另外一种微分（余微分）的话，就得到 current vector $J$ ，即流向量。用下面两个简单的式子，就把 Maxwell 方程写出来了， $d A = F$ , $\delta F = J$ 。

普通你要念电磁学的书的话，当然需要了解电磁的意义。我不了解。但是要了解电磁学的意义，把方程全部写出来的话，书上往往是一整页，种种的微分呀什么的讲了一大堆。其实简单地说，也就是平行性的微分是场的强度，而场的强度经过某个运算就得到它的流向量。这就是 Maxwell 方程，与原来的完全一样。所以 Maxwell 方程就是建立在一维的纤维丛上，不过是一个复一维的纤维丛。

你怎样把每个纤维维拼起来呢？我们需要群的概念。有一个群，群里有一个运算，把一个纤维可以挪到其它一个纤维。纤维如果是一维的，即使是复一维的话，我们需要的群仍旧是可交换的群，叫做 Abel group，杨振宁先生了不得。他可以用到一个非 Abel 群，也很简单，我们叫做 SU（2）群。用 SU（2）connection，把同样的方程式写出来，就是 Yang - Mills 方程， $D A = F$ ， $\delta F = J$ 。

这有不得了的重要性。我们搞几何学的人觉得有这样的关系，物理学家说你这个关系跟物理有关系，这是非常困难的，并且有基本的重要性。比方说像去年获诺贝尔奖的，我想大家都知道崔琦的名字，做理论方面的所谓 Hall 效应，也用到我们这些工作。

我们说我们专搞曲率。你要开一个车，路如果弯得多了的话你就要慢下来，直的话你就冲，这就是曲率。曲率要是在高维就比较复杂了，不过也是一些代数，并且可以做得很巧妙。我的一个朋友，也是学生，叫 Simons。我们所做的工作就是曲率，就对崔琦跟他们一群得诺贝尔奖的有好处。所以一般讲来，在房子里我们只管扫地，想把房子弄弄干净，弄弄清楚，然后有伟大的物理学家来说你们这个还有道理（大笑，掌声），这个我们也很高兴。

几何学在其他领域的应用

现在几何不仅应用到物理，也应用到生物学中。讲到 DNA 的构造，是一个双螺线，双螺线有很多几何，许多几何学都在研究这个问题。现在许多主要的大学，念生物的人一定要念几何。现在有很多人研究大一点的 compound，这是分子，是由原子配起来的。原子怎么个配法就是几何了。这些几何的观念不再是空虚的，有实际上的化学的意义。

数学的独特性与总结

数学比其它科学有利的地方，是它基本上还是个人的工作。即使在僻远的地方，进步也是可能的。当然他需要几个朋友，得切磋之益。谢谢大家。（极其热烈的掌声）

本文载于 “赛先生” 公众号，源自求是科技基金会官网。“数学大院” 经授权编辑整理发布。

我的几何人生

丘成桐数学大院 2024 年 12 月 21 日 19:59 北京

丘成桐｜撰文

童年与父亲的影响

月前我在汕头参观了我出生的小洋房。这小洋房是我父母新中国成立前购置，作为我们一家人居住的。75 年的老房子经汕头市大修得以重睹，非常感激人民政府的厚爱。

我也见到父亲走过的路。我发觉它和我一生走过的路、想要做的事情，何其相似！只是大时代的走向不一样，我比他幸运得多！

父亲成长于粤东蕉岭的农村，在祖父去世后生活艰苦的条件下，到厦门大学学习政治经济学，随后东渡留学日本早稻田大学。回国后正值日寇侵华，父亲奔走广东、福建、江西 3 省 30 多个地方，奋力抗日救国。

抗战胜利后，他帮助联合国救济总署在潮汕地区散发救济物品。这是个肥缺，但父亲清廉自持，不同流合污。

后来，我们一家人到了香港，我在新界元朗的农村长大，父亲在几所大专院校任教，其中一间叫崇基书院，是香港中文大学的前身。开始时父亲研究中国哲学，要从基础上认识中国文化。为了彻底了解中国儒道，他花了很多时间去研究西方哲学及印度佛学，和中国哲学比较，希望能揭橥中国文化的精髓。

1969 年，丘成桐在香港中文大学崇基书院毕业典礼上

我们一家 10 口，生活由父亲一人独支，肩负之重可以想见。但他仍然对教学充满热情，并常常写作直至深夜。他每个星期都会在家中向诸生讲述哲学，我虽不懂，但在不知不觉之间，东西哲学的精神在我心中已经产生了潜移默化的作用。

父亲一生为国，为了国家愿意舍弃一切。作为读书人，他不畏强权，不为富贵所屈。他秉持读书人的气节，颠沛中以读书思考为乐，直至英年去世，不改其志！

我现在年过七十，回顾走过的路，和父亲何其相似。只不过我屡遇明师，才有所成就。父亲去世后这 61 年，祖国经历了巨大的变化，改革开放大大地改变了整个社会，教育不断提升，国家欣欣向荣，华侨在海外也得到保护。

数学之路的启蒙

我 13 岁得到父亲的鼓励，开始对数学发生兴趣。父亲对我标示从哲学高台看众学的重要观点，海纳百川，而又要脚踏实地、虚怀若谷，以成就不朽之业。为学需要标心于万古之上，送怀于千载之下。这样的胸怀，对我一辈子的行事为人，影响甚深。

然而好景不长，次年父亲去世。对年幼的我可谓晴天霹雳！一家人顿失支撑，家无居留之所，食无隔夜之粮，前途茫茫，情何以堪？

幸赖母亲坚持，学业得以继续！

母亲在全家极度困难的时候，还坚持让我们上进，让我有机会去追寻我父亲向往的不朽之业。直至今天，我还记得她慈祥却是坚定的目光。

10 岁时，父亲教我古文，第一篇是《礼记・檀弓下》的《嗟来之食》，第二篇是陶渊明的《五柳先生传》。

以后我才知道父亲在教我做人的道理。第一篇告诉我们做人的尊严，富贵不能淫，贫贱不能移，威武不能屈。第二篇描述陶渊明好读书，不求甚解。研求之乐，使我一生受用不尽。

父亲写他的《西洋哲学史》，在引言中引用《文心雕龙・诸子》：“嗟夫！身与时舛，志共道申，标心于万古之上，而送怀于千载之下！”

在学问上能够做出不朽的工作，这个宏愿一直激励着我。

丘成桐全家福，1955 年摄于香港沙田。前排左一为丘成桐

正如 “孔子厄于陈蔡”，不朽的工作，不可能都是坦途，所以父亲说：“寻孔颜乐处，拓万古心胸。”

做学问要达到这个境界，要学孟子说的：“我知言，我善养吾浩然之气。”

一个人的际遇，对生命的领会，会影响到我们对美的追求，对真理的认识。

所以太史公年轻时遍历天下名山大川，访寻古代遗迹民情，始得天人之际，成一家之言。

我喜欢历史，它使我增加对人生的经验，我也喜欢《史记》《左传》的文字，直抒胸臆，令我情不自已。以后我做科研遇到困难时，会朗诵秦汉古文，也会诵咏诗词，它们使我心旷神怡，回观科研，竟然若有所得。

逆境中的坚持与成长

丘成桐带领清华大学求真书院同学们游学了解中国历史

人生的经历，不可能都是顺境，科研也如此。没有经过逆境而得到的成果，一般来说，深度总会不够。

《红楼梦》是一部伟大的作品，它花了很大的功夫去描述一个大家族的荣华富贵，通过一群妙龄女子和贾宝玉吟咏风月的爱情故事，又通过贾蓉父子、刘姥姥、尤二姐的眼睛和行止，描述秦可卿和王熙凤的种种，指出家族的问题。

小说最动人心弦的部分，却是这个大家族最后的破落。小说通过凄美的爱情故事、奢侈浮华的贵族生活、封建社会对年轻男女的桎梏，呈现大家族破落的原因和经过，引起大家深深的共鸣。

我第一次读《红楼梦》时 11 岁，入世不深，对书中这些男女的行为甚为不解。父亲又要求我背诵其中的诗词，初时觉得辛苦。但是在父亲去世后，我心情相当波动，也开始了解人情冷暖，家庭经济极度困难，能否继续读书成为一个重要的问题。

家庭经济产生的种种问题以外，我丧失了精神上的支柱！以前父亲告诉我做人的道理，做学问的方向，我一直跟随他的步伐，深信不疑。但是他不在了，我必须自己做决断。在极度哀伤的心情下，我决定继承父亲的遗志，这辈子必须要做出一番不朽的事业，因此必须继续我的学业。

为了能够按时交学费，我必须忍受别人的歧视，必须承接别人的白眼。在这个时候，才终于体会到孟子说的：“独孤臣孽子，其操心也危，其虑患也深”。

我在念高一那一年，对历史特别感兴趣，阅读吕思勉先生的《中国通史》，开始了解中国古代的历史，也培养了我的家国情怀。在书中的最后一页，吕先生引用了梁启超翻译的英国拜伦的诗篇，是拜伦在希腊看到波斯古墓而吟咏的作品，中间有句说，“难道我为奴为隶，今生便了？不信我为奴为隶，今生便了！” 这首诗一直在鼓励我向上。

我决定要在学问上出人头地，当时实在没有其他道路可走。我可以望尽天涯路，但是我必须解决眼前的经济问题。最简单的办法是替学生补习数学，争取给家庭一点补助。我走遍了香港岛、九龙各地区，上门教授学生，我的第一个学生只低我一年级。收入也很微薄，但我还是兴致勃勃地去做。有时要走相当长的山路。为了争取时间读书，一路上拿着书本看，有时候也思考数学的问题。

当时我读遍了能找到的数学书籍，有些书籍是从吃饭钱省下来到旧书档买的。这些书并不连贯，要看运气，都是从内地运出来的，有些是中学用书，有些则是大学用书。这样子念着，虽然不求甚解，但努力用功，还是有不少裨益。

当时没有图书馆，我常跑到市区中的书店，站在书架前看书，一看就是一个多钟头！书店老板居然没有阻止我，大概是认为我好学不倦吧。

需要说的是，我看的书不是准备高考的书，任何有意义的书我都会阅读。我养成了一个习惯，无论到什么地方，我总会带着一本书，一有空就拿出来看。

尽管我在中学名列前茅，但没有得过任何奖项，我不在乎。我始终没有忘记人生的目标是成就不朽的学问。我也很清楚，如果我长期在当时的香港，顶多做个井底之蛙，香港的老师们，不可能带领我望尽天涯路。到了大学的时候，我数学的水平已经远超同侪，但是我觉得没有什么值得骄傲的地方，因为这个不是我的目标。

学术生涯的转折与成就

念大学时，我常到图书馆借书看，但是那里书并不多，也不知道主流学问的方向，走了很多冤枉路。幸好得到一位年轻老师的赏识，推荐我到加州大学伯克利分校，最终师从陈省身先生。这可以说是我做学问最大的转折点！

1969 年 9 月 1 日，丘成桐怀揣着从朋友借来的 100 美元辗转飞往旧金山，这是他第一次乘坐飞机。

陈先生的名字我早有所闻。父亲去世那年，《明报月刊》转载了一篇文章，是陈先生的简要自传，叫作《学算四十年》。

看了文章，我才知道中国有数学家在海外出人头地，甚至还有如陈先生这样完成不朽之业的大师，这使我茅塞顿开，有大丈夫当如是的感觉。现在在他做学问的地方念书，教授中又不乏大师，我的精神至为振奋！

我在伯克利的第一年，陈先生到外地休假去了，但是围绕在我旁边的都是良师益友。老师有非线性微分方程大师查尔斯・莫里（Charles Morrey）、拓扑学大师埃德温・斯帕尼尔（Edwin Spanier）；年轻教授有布莱恩・劳森（Blaine Lawson）、凯伦・乌伦贝克（Karen Uhlenbeck）、多里安・戈德菲尔德（Dorian Goldfeld）、鲁弗斯・鲍恩（Rufus Bowen）、伍鸿熙；同学则有比尔・瑟斯顿（Bill Thurston）、比尔・米克斯（Bill Meeks）、约翰・米尔森（John Millson）、郑绍远等，真可谓一时之盛！

在这样的环境下，我在当年冬假 20 岁时完成了人生中第一篇比较有意思的论文，这篇论文在我 21 岁那年夏天发表在《数学年刊》（Annals of Mathematics）上。

1983 年，丘成桐于波兰获颁菲尔兹奖。

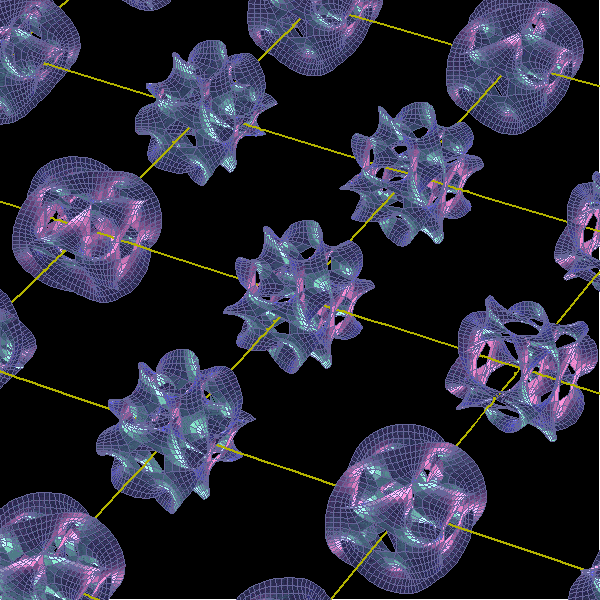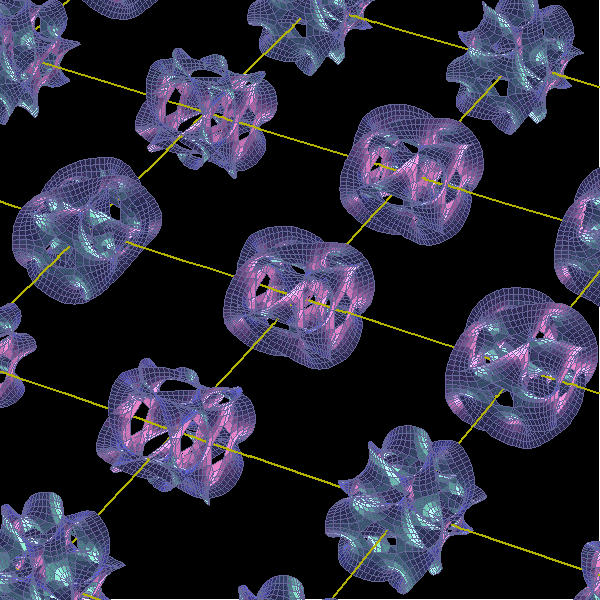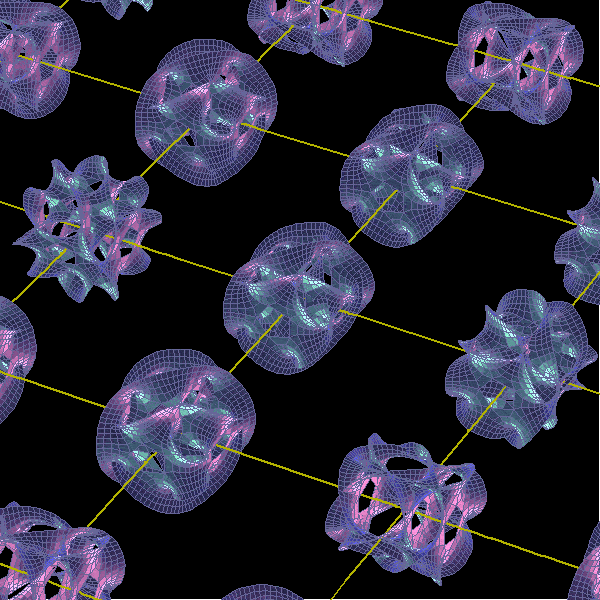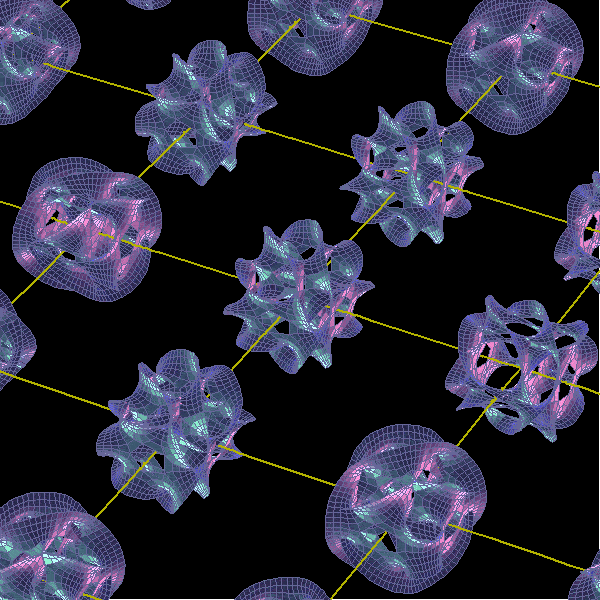
卡拉比 - 丘流形动态图

陈先生刚好休假回来，见到我的时候，一脸笑容，大概是高兴没有押错宝吧。毕竟我在香港中文大学还没有毕业，由他力挺，进入了伯克利的研究院，虽然他是大教授，难度也还是不小的。他回到伯克利后，我请求他当我的博士指导老师。

他对我期望很高，一开始就要我解决黎曼猜想，作为博士论文的题目。但是我对这个题目的兴趣不大。陈先生是很宽容的导师，大概见我没有继续和他讨论这问题，就放弃了要我朝着这个方向走。

过了两个月后，他要求我在他的几何讨论班演讲，介绍我刚到伯克利时做的文章。这是一个很著名的几何讨论班，能够在讨论班上做演讲是个荣誉。

当天来了 50 多位听众，讲堂挤得水泄不通。听众中有约瑟夫・沃尔夫（Joseph Wolf）教授，他是陈先生在芝加哥大学时的博士生，是我演讲题目的专家，看来他很满意我的工作。

过了两天，陈先生叫我到他的办公室，告诉我可以毕业了，着实让我吓了一跳。

我自问学问还是不够扎实，还需要学习，但又考虑到香港家人经济不好，早一点毕业，可以让母亲和兄弟姊妹生活舒适些，所以听从了陈先生的建议。

我师从陈先生，学习了复几何的陈氏特征类，对我的学问有裨益。陈先生 60 岁那年，在我行将毕业时，送了一本他写的书给我，书名叫《不具位势原理的复流形》（Complex Manifolds without Potential Theory）。他在书中亲题赠言，说：“余生六十矣，薪传有人，愿共勉之。”

这几句话使我受宠若惊。30 年后，我写了一副对联给陈先生，中间有句叙述此事：“留书赠言，墨迹犹在，相期未负平生。”

陈省身在赠与丘成桐的书中扉页写道：“余生六十矣，薪传有人，愿共勉之。”

我父亲早逝，陈先生无论在学问还是在事业发展上的教导，都继续了我父亲的遗训，影响了我一辈子。

但是，正如我少年时没有全部听从父亲的教导一样，我喜欢探索自己的研究方向。研究院一年级时，我师事莫里先生。受他启发，我决定要以新的观点来研究几何学，利用非线性微分方程去构造几何结构，也通过几何的观念来研究非线性方程。以后郑绍远、孙理察（Richard Schoen）、凯伦・乌伦贝克、莱昂・西蒙（Leon Simon）、克利福・陶布斯（Clifford Taubes）、理查德・汉密尔顿（Richard Hamilton）、李伟光（Peter Li）等人都有同样的想法。我们共同努力，解决了一大批重要的问题。

我们创立的这个学科被称为几何分析（Geometric Analysis），直到如今，它还是数学中最重要的分支之一。

这个分支的开花结果，得到的成就，可以说无愧于先人，可以传诸后世矣！