KPCA核主成分分析法C++程序测试

传统的PCA可以从线性可分的特征中提取主要特征，但是线性不可分部分的信息直接被抛弃了，但其实有很多信息虽然在样本空间是线性不可分的，但是映射到高维的核空间之后是线性可分的，这部分信息在分类识别的时候也是非常重要的，为了提取这部分信息特征，就必须采用KPCA的方法。

KPCA的简介:

在一个样本空间中，有些数据是线性不可分的，但是当通过一种方法把它映射到高维空间之后，它却有可能变成线性可分的数据。如下图所示，要在一维空间中做线性分割，即通过一个点把红色和白色的区域分割开来，这个不可能的，即线性不可分。但是通过函数f(x)=(x-x0)(x-x1)把数据映射到二维空间之后就成了一条抛物线，在二维空间中做线性区分，即通过一条线把红色和白色区域分开，就可以实现了。依次类推，在二维空间中通过一条线无法分开的数据，当映射到三维空间之后，可能可以通过一个平面轻松的分开。这就是做核空间映射的根本目的。

但是，随着空间维数的增加，运算量也迅速增加。为了减少运算开销，就需要把在核空间的线性运算转而用样本空间的核函数来表示。

KPCA的主要思路:

(1)将样本数据从样本空间作非线性映射到核空间，以此来增强数据的线性可分性。

(2)将核空间的线性操作全部化为矩阵内积的形式。

(3)将核空间的内积全部用样本空间的核函数或者核矩阵来代替。

(4)用核函数的形式进行子空间降维的操作。

KPCA的步骤：

(1)针对训练集S，给定一个核函数k。

(2)计算出核矩阵K，再计算出~K(中心化的K)。

(3)求~K的特征值和单位特征向量，将特征值从大到小排列，提取前D个特征向量，并令，降维矩阵为

。

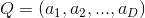
(4)对于任一样本向量x，通过KPCA降维后的数据为：。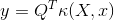

核矩阵K的计算方法：  ； 

~K计算方法：

主程序部分代码：

完整Qt工程下载：http://download.csdn.net/detail/u013752202/9252849

#include <QtCore/QCoreApplication>
#include "kpca.h"

int main(int argc, char *argv[])
{
    QCoreApplication a(argc, argv);

    cout<<"=========KPCA Start=========== "<<endl;
    int i,j,t;
    int m,n;//数据大小，m为行数样本个数，n为列数样本维度
    const char *File="src.txt";//待降维数据文件
    const char *eigenvectors="eigen.txt";//特征值和特征向量存储文件
    const char *projectfile="kpcaproject.txt"; //KPCA降维结果文件
    double eps=0.000001; //jacobi方法的终止精度
    double gaussparameter;//高斯核函数参数sigma
    double getratio=0.90; //提取特征值的最高累计贡献率
    KPCA kpca(3,2);
    Mat src=kpca.getdata(File);//获取外部数据
    m=src.rows;
    n=src.cols;
    double A[m],B[m];//m维向量
    KPCA testkpca(m,n);//声明一个KPCA对象
    //=============求中心化的高斯径向基核矩阵=================
    //gaussparameter=testkpca.getSigma(x,m,n,l,100,800);//计算最佳的高斯径向基参数sigma
    gaussparameter=392;//计算时间很长，计算好了之后就直接赋值
    cout<<"gaussparameter  is "<<gaussparameter<<endl;
    Mat K=testkpca.getkernelmatrix(src,gaussparameter,1);//高斯核矩阵
    Mat KL=testkpca.modifykernelmatrix(K); //修正核矩阵
    Mat fvalue(m,m,CV_64FC1);//m维方阵fvalue,特征值
    Mat fvector(m,m,CV_64FC1);//m维方阵fvector,特征向量
    //=========求特征值和特征向量==========
    for(i=0;i<m;i++) //fvalue = KL
        for(j=0;j<m;j++)
            fvalue.ptr<double>(i)[j]=saturate_cast<double>(KL.ptr<double>(i)[j]);
    i=testkpca.jcb(fvalue,fvector,eps,10000);//求取特征值和特征向量
    cout<<"计算特征值的迭代次数: "<<i<<endl;
    if(i!=-1){
        for(i=0;i<m;i++)
            A[i]=fvalue.ptr<double>(i)[i]; //获取特征值
    }
    else
        cout<<"不能求得特征值和特征向量"<<endl;
    //=========正交规范化特征向量========
    testkpca.zhengjiao(fvector);//这里是用的施密特正交法，运算很慢，还可以优化
    //=========选取主成分===============
    testkpca.saveeigenvectors(A,fvector,eigenvectors);//保存特征向量
    testkpca.selectionsort(A,fvector); //特征值和特征向量排序
    t=testkpca.selectcharactor(A,getratio,B); //提取特征值
    cout<<"特征值的累计贡献率："<<endl;
    for(i=0;i<m;i++)
        cout<<B[i]<<"  ";
    cout<<endl;
    cout<<"选择累计贡献率："<<getratio<<endl;
    cout<<"保留主成分个数："<<t<<endl;
    //=======求KPCA的结果并保存为文件======
    Mat Project;
    if(t>=1&&t<=m)
        Project=testkpca.getProject(t,KL,fvector);//计算投影
    else
        cout<<"error"<<endl;
    testkpca.saveProject(projectfile,Project,t);
    cout<<"Project:"<<endl;
    cout<<Project<<endl;
    cout<<"==============KPCA End============="<<endl;

    return a.exec();
}

运行结果分析：

下图中红框框住的是保留主成分的贡献率，保留的主成分为6个。

特征值和特征向量如下图：

最后降维的结果如下图：

KPCA输入的样本为一个8*177的矩阵，共有8个样本，每个样本的维度都是177维。

得到的特征值有8个，特征向量8个。

保留了6个主成分，降维后的矩阵为8*6，从177维降维了6维。