c++使用主成分分析（PCA）

主成分分析（PCA）

PCA原理

PCA(Principal Component Analysis)，即主成分分析方法，是指通过降维的方法将数据的多重指标转换为少数几个主要的综合性指标，进而利用几个较少的变量研究整个数据集，从而实现化繁为简的一种数据处理算法。
PCA提供了一种将高维空间中的点在低维子空间中表达的方法。给定数据$$a_i\in R^p,i=1,2,...,n,$$
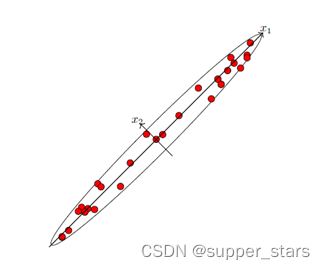
其中n表示样本数，定义 $$A=\left[a_1,a_2,\cdot \cdot \cdot ,{\mathrm{a}}_n\right]$$。我们假设A的行和为0（否则可以逐元素减去该行元素的平均值，这不会改变数据的相对结构，只是在 空间沿着坐标轴进行了平移）。主成分分析的思想是寻找样本点方差最大的若干方向构成的子空间，之后将数据点投影到该子空间内来实现降维。如下图所示，给出了R2中的一组数据点，可以看出数据点沿着方向x1的变化最大。在这个例子中，主成分分析方法就是确定黑色实线，然后将数据点投影到x1来进行降维。

假设我们想要将 Rp中的数据点集 { a i } i = 1 n \left\{ {{a_i}} \right\}_{i = 1}^n {ai​}i=1n​投影到 的一个d维子空间(d<p)中，记 $$X\in R^{p\times d}$$为该子空间的标准正交基形成的列正交矩阵。易知，数据点ai在子空间的投影为$${\mathrm{P}}_X(a_i)=X{X}^T{a}_i$$ 。根据主成分分析的基本思想，我们需要寻找最优的X ，使得投影后的数据点集 { P X ( a i ) } \left\{ {{{\rm{P}}_X}({a_i})} \right\} {PX​(ai​)}的方差最大。根据零均值假设，投影后数据点集的协方差矩阵为$$\frac{1}{n}\sum _{i=1}^{n}X{X}^T{a}_i{(X{X}^T{a}_i)}^T=\frac{1}{n}X{X}^{T}A{A}^{T}X{X}^T$$
而多元分布的方差大小可由协方差矩阵的迹来刻画，因此，得到优化问题$$\max Tr(X^{T}A{A}^{T}X),s.t.X^{T}X=I$$
其中利用了Tr(·)的性质$$Tr(X{X}^{T}A{A}^{T}X{X}^T)=Tr(X^{T}A{A}^{T}X{X}^{T}X)=Tr(X^{T}A{A}^{T}X)$$
可以证明，上述问题等价于求解$$A{A}^T\in R^{p\times q}$$从大到小排列的前d个特征值对应的特征向量。

PCA应用

//----------------------------- pca计算主方向 ----------------------------
	pcl::PointCloud<pcl::PointXYZRGB> cloud;
	Eigen::Vector4f pcaCentroid;//质心
    pcl::compute3DCentroid(cloud, pcaCentroid);//计算质心
    Eigen::Matrix3f covariance;//协方差矩阵
    pcl::computeCovarianceMatrixNormalized(cloud, pcaCentroid, covariance);
    Eigen::SelfAdjointEigenSolver<Eigen::Matrix3f> eigen_solver(covariance, Eigen::ComputeEigenvectors);
    Eigen::Matrix3f eigenVectorsPCA = eigen_solver.eigenvectors();//计算特征向量
    Eigen::Vector3f eigenValuesPCA = eigen_solver.eigenvalues();//计算特征值
    eigenVectorsPCA.col(2) = eigenVectorsPCA.col(0).cross(eigenVectorsPCA.col(1)); //校正主方向间垂直
    eigenVectorsPCA.col(0) = eigenVectorsPCA.col(1).cross(eigenVectorsPCA.col(2));
    eigenVectorsPCA.col(1) = eigenVectorsPCA.col(2).cross(eigenVectorsPCA.col(0));
    std::cout << "特征值va(3x1):\n" << eigenValuesPCA << std::endl;
    std::cout << "特征向量ve(3x3):\n" << eigenVectorsPCA << std::endl;
    std::cout << "质心点(4x1):\n" << pcaCentroid << std::endl;
    Eigen::Matrix4f tm = Eigen::Matrix4f::Identity();
    Eigen::Matrix4f tm_inv = Eigen::Matrix4f::Identity();
    tm.block<3, 3>(0, 0) = eigenVectorsPCA.transpose();   //R.
    tm.block<3, 1>(0, 3) = -1.0f * (eigenVectorsPCA.transpose()) *(pcaCentroid.head<3>());//  -R*t
    tm_inv = tm.inverse();//逆
 
    std::cout << "变换矩阵tm(4x4):\n" << tm << std::endl;
    std::cout << "逆变矩阵tm'(4x4):\n" << tm_inv << std::endl;
 
    pcl::PointCloud<pcl::PointXYZRGB>::Ptr transformedCloud(new pcl::PointCloud<pcl::PointXYZRGB>);//旋转点云
    pcl::transformPointCloud(cloud, *transformedCloud, tm);//变换
	//计算质心
	Eigen::Vector4f pcaCentroid1;
    pcl::compute3DCentroid(*transformedCloud, pcaCentroid1);
	std::cout << "质心“:\n" << pcaCentroid1 << std::endl;