主成分分析(Principal Component Analysis)
我们来形式化的描述一下PCA的思想
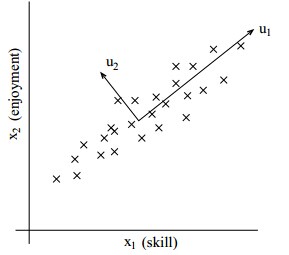
图中描述了一组二维的数据,但同时我们可以看出在u1方向上的数据已经可以描述数据集的大部分的信息,因此可以将二维的数据映射到u1方向上,实现降维。
在实现pca算法之前要进行一些预处理:
1. 计算数据的均值
2. 将每一个数据减去均值
这两步规约化了数据,保证数据的均值为0。
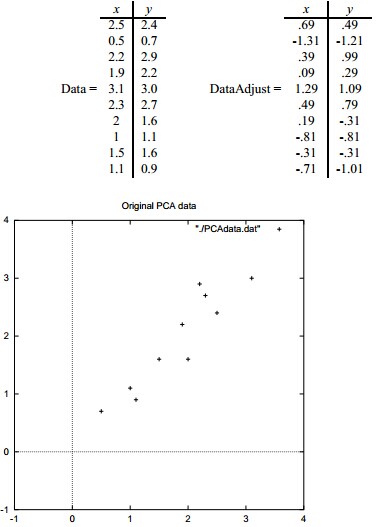
上图的左边是原始的数据,右边是调整之后的数据,下面是数据集在坐标轴上的表示,这里用二维的数据进行演示。
3. 计算协方差矩阵
4. 规约化数据集的方差
第三步为之后计算特征值特征向量做准备,第四步保证了各个维度的数据方差是一样的。当然可以想到协方差矩阵是对称的,所以一定存在满的特征值。
对于上述的数据协方差矩阵为:
那么怎么挑选合适的U,能最大化代表原始数据的信息呢?我们看两组例子:
很明显,左图的数据有一个相当大的方差,映射后的数据离中心点都很远,右图则恰恰相反。所以,我们就可以想象到,最大化投影的距离,对于u,也就是最大化:
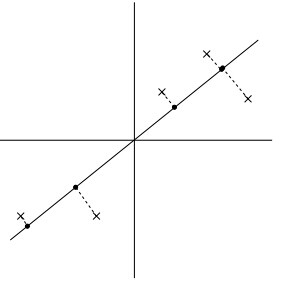
我们可以看出,最大化上述公式其实就是给出协方差矩阵主要的特征向量。如果我们想将数据映射到k维的子空间,就挑选协方差矩阵里较大的k个特征向量u1, . . . , uk,对于我们具体样例,求得特征值和特征向量为:
挑选完特征向量之后,新的样本:
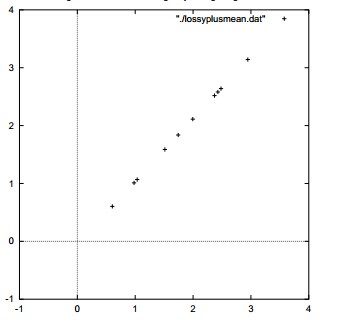
重新绘制一下,就得到了下图,样本已经在一条线上了:
下面给出一个pca在计算机视觉方向的应用:
还有用于视觉的重构,下面是一个不同光照条件下的照片:
我们使用五中主成分就可以重构成细节更多的图片
奇异值分解(Singular Value Decomposition)
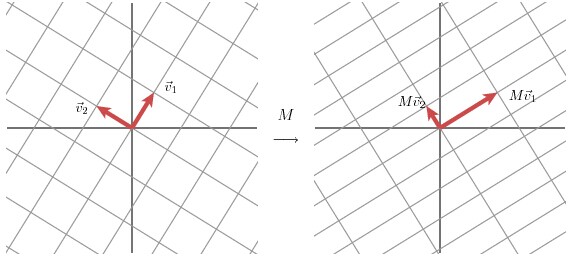
我们以2x2的矩阵为例,我们找到一组正交的单位向量v1和v2,则Mv1和Mv2也是正交的
令u1和u2是Mv1和Mv2方向上的单位向量,σ1 和σ2分别是其长度,这些数就被称为M的奇异值。所以有:
对一个向量x,有
然后
点积v·x=vTx
之后可以推导出:
可以表示为:
U的列向量为u1与u2,Σ是对角矩阵,值为σ1 和σ2,V的列向量为v1与v2
另一种解释是这样的:
U的列向量是AAT的正交特征向量。V的列向量是ATA的正交特征向量。AAT的特征值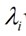
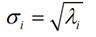
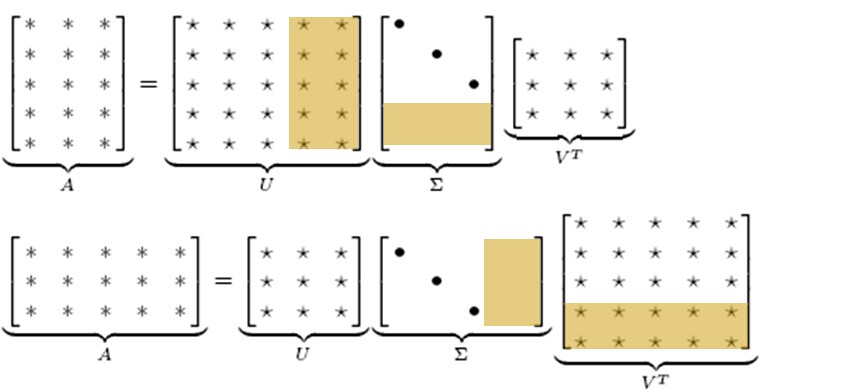
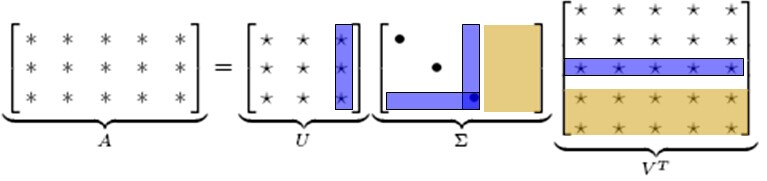
SVD的降维原理为:
计算的结果如下:








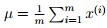
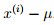
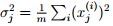
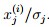

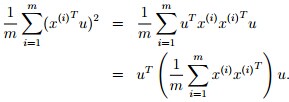
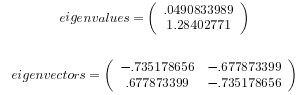
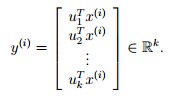



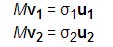
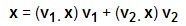
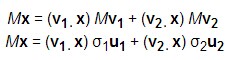
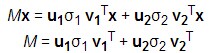
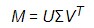
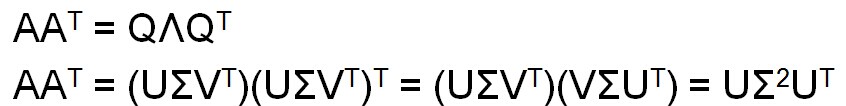
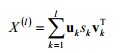














 815
815

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








