DirectX12（D3D12）基础教程（十八）—— PBR基础从物理到艺术（中）

5、物理光学——光照方程的推导

5.1、光子能量（辐射能）

  现代，我们知道很多粒子都是具备能量的“量子”，而根据最初普朗克关于能量量子化的假设，即最著名的普朗克方程：
$$\begin{gathered} E=h\nu \\ 式中E为量子能量，h为普朗克常数，\nu 为频率，对于光子来说这就是光波的频率。 \\ h=6.62620\times 10^{-34}焦耳\cdot 秒 \end{gathered}$$
  根据这一基本方程（其实物理中著名的或者说重要的方程都是基于能量变换形式的），并基于我们知道的一些基本物理知识，我们将其应用于“光子”来看看：
$$\begin{gathered} E=h\nu =\frac{hc}{\lambda } \\ 式中c为光速，\lambda 为光波长，因为c=\lambda \nu \\ 真空中：c=2.998\times 10^8米/秒 \end{gathered}$$
  即光速等于波长乘以频率，这也就是高中时我们学过的关于一般波的速度频率波长之间的关系，也就是说光子的能量与频率成正比，与波长成反比。在这里需要进一步的理解的是说，一般光速是恒定的（不同介质中光速略有不同），所以一旦知道光波的波长就等于知道光波的频率，反之亦然。又因为光子的能量正比于频率，所以知道了光波的波长也就等于知道了光波的能量，因此实际讨论或计算中，我们只需要提及一个量即可，按照惯例，对于光来说通常我们提的都是波长，当然可能是因为波长单位比起频率单位来说更容易让人理解所致。

  这里稍微扯些题外的话题，根据前面的普朗克方程，接着再引用知名的爱因斯坦质能方程，就可以推出如下关系：
$$\begin{gathered} E=h\nu ,E=m{c}^2 \\ \nu =\frac{1}{h}m{c}^2 \\ \lambda =\frac{c}{\nu }=\frac{h}{mc}=\frac{h}{p} \end{gathered}$$
  根据这些结果，也就是说如果我们知道了物质的质量，那么就等同于知道了物质的“本征频率”，因为其它的量都是常数，也就是说物质的本质也是“波”！（你可以据此根据你的体重计算一下你的“本征频率”，以判断哪些游乐场的游戏是不适合你的:-）而这正是量子物理先驱之一——德布罗意当年推导的结果，而最后一个波长-动量的关系就被称之为德布罗意公式。因为并不是所有的粒子都能以光速运动，所以德布罗意公式中用动量代替了质量与速度的乘积。而根据这些公式又可以反算出光子的相对论质量（波粒二象性！），大家可以计算一下，但要注意的是光子是没有静止质量的。（这部分内容，有兴趣的同学可以去看看量子力学。）而正是这些简单的公式深刻的揭露了物质与能量本质上是一致的物理含义，同时也暗示了物质具有“波粒二象性”的深刻物理本质，所以万事万物皆处于永恒的运动之中！

  对于一般的可见光来说，普遍认为的波长是在400纳米至700纳米之间，当然对于女生来说这个范围可能是380纳米至720纳米之间，所以女生对色彩的感知度要高于男生！基于此并结合上式，可以算出：
$$\begin{gathered} hc=1.9865\times 10^{-25}焦耳\cdot 米 \\ \lambda =390+10^{-9}\sim 700+10^{-9}米 \\ E=\frac{hc}{\lambda }=5.0936\times 10^{-19}\sim 2.8379\times 10^{-19}焦耳 \end{gathered}$$
  瞧，不费吹灰之力（当然建议你按下计算器），我们就知道了可见光范围内的光子能量的大小！当然对于“一个个”光子来说，这点能量简直是小的可怜，但是对于大的发光体来说，几乎在每个瞬间，都会辐射出如恒河沙数般的光子，所以如太阳这样的发光体，每时每刻都在辐射出巨大的能量！（注意这里其实隐含说明了量子化的本质，虽然太阳光能巨大，而且感觉上是连绵不绝的，但最终在极微观的尺度上确是由一个个“光子”组成的，因为光子在传播的过程中频率是极不容易改变的，所以一旦光子在生成时频率确定了，那么其能量也就确定了。）

  当然对于我们实际的渲染计算来说，之前的这些计算帮助还并不大，唯一有帮助的就是不同光波长（或频率）反应在人眼中是不同的颜色：

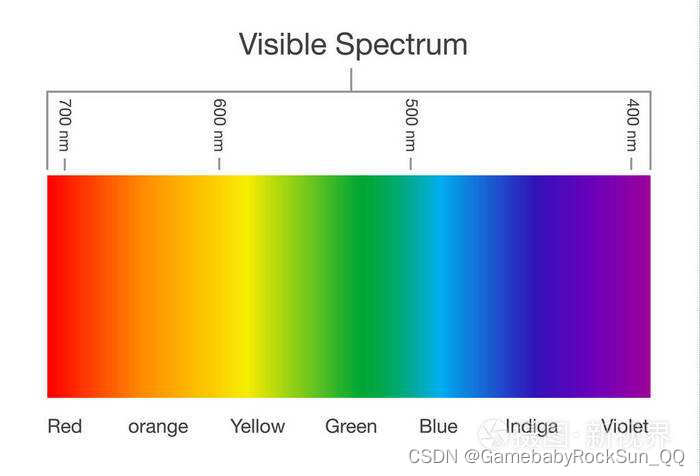
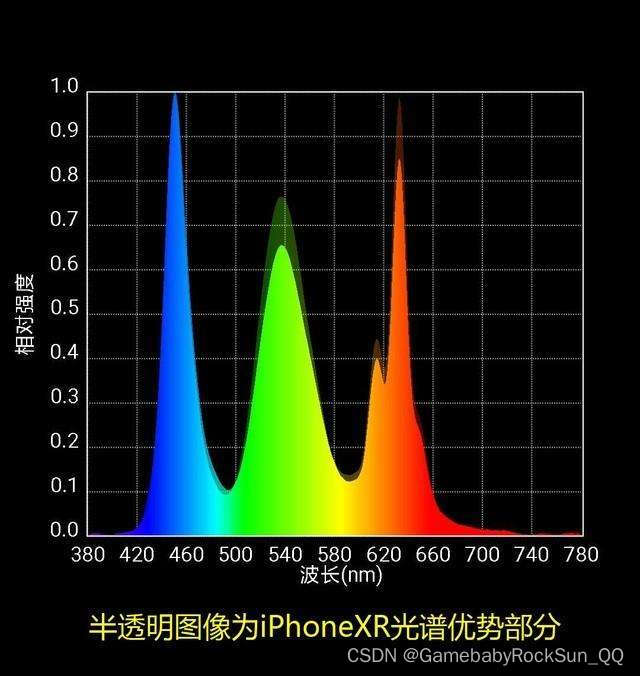
  下图是太阳光谱，纵坐标是辐射强度的比例（如果下图作为男生的你能够轻易的分辨出从左到右的每种细分颜色，那么恭喜你，你的色彩感很强，可以直接跟小姐姐聊关于口红色号的问题了，那么女生请划过）：

  而下图则是典型的LED屏的辐射比强度图，可以明显看出显示器屏幕只是使用RGB三原色的基本原理，当然这么窄的光谱条，实际上对我们的眼睛是有极大伤害的。

  当大家看到这里的时候，其实PBR的核心机密就得到了解答，也就是说为什么我特别讲PBR其实是基于“能量”计算的渲染了。根据上面这些知识，首先我们了解了世界色彩的本质，其实就是光波的波长，其次知道了波长就等同于知道了能量，再次光的本质其实就是能量！所以综合起来，人们最终能够看到真实世界中的色彩信息，是因为我们感知到了光的能量！因此PBR渲染就真正回归了我们模拟五彩缤纷的真实世界的本质，也就是面向“能量”的渲染，而物理学研究的核心本质就是研究能量变化的规律，所以PBR也被自然的被称之为基于物理的渲染。

  至此，我们用到的知识还不是很多，但请在继续之前，一定要理解和掌握这些基本原初的简单方程，因为前方高能！

5.2、RGB表达的含义

  对于计算机来说，虽然上面的光谱可以模拟出来，但并不是基于我们之前介绍的“光子”能量方程的，图中也看不出“能量”。在计算机中，我们都是使用RGB三原色理论来近似混合模拟每种色彩的光，也既不同波长的光波：

  在计算机中要进行运算表达时，一般使用0~255之间的整数表示一个颜色分量，最终形成一个 $RGB(0\sim 255,0\sim 255,0\sim 255)$ 的向量表示每种颜色，当然这是最基本不过的知识了，这里要告诉大家的是，请你一定结合前面推导的光子能量方程，将RGB颜色直接理解为光的辐射能大小的“离散表示”，或者直接理解为是光能量（光波长）大小的采样值。这是与你之前学习的基本知识在理解上是完全不一样的。当然在Shader渲染中，我们一般用float分量0.0f~1.0f之间的值来表示RGB分量。需要注意的是，有时候为了PBR渲染来说，颜色float值的范围可能还会大于1.0f ，以表示更高的能量。

  无论那种表示方法，最终从此刻开始我们都要将RGB理解为“光子的能量”大小！记住这点很重要，因为在后续的PBR计算中，会直接将RGB的值带进去进行计算。因此无论从颜色的角度，还是从能量的角度来说后续的一些计算一下子就都说的通了，所以如果你能将RGB颜色理解为光能量“量子”的大小的话，对于理解整个PBR将有莫大的好处！

5.3、辐射通量（辐射功率）

  当然知道了光能量的基本方程和RGB近似之后，目前来说我们对物理光照的模拟还是无能为力的，所以我们需要继续推导。那么让我们来思考一个问题，那就是如果光辐射是能量，那么作为“瞬时模拟”来说（3D渲染的本质就是一帧帧模拟光照，类似于一张张给场景拍照，需要的是瞬时的光照效果），我们需要先搞清楚什么？

  ok，如果你有中学阶段的物理知识的话，一定会想到瞬时的能量，不就是“功率”吗？如果你想到了，那么恭喜你，你果然是“理工男”！只是在这里，我们需要加入些微积分的知识来进一步表达方程了，即一般的能量-功率微分方程：
$$\begin{gathered} 辐射通量(辐射功率): \\ \Phi =\frac{dE}{dt} \\ 单位:焦耳/秒,J\cdot s^{-1}=瓦W, \end{gathered}$$
  这个方程看上去挺吓人，其实表达的意思就是说，所谓功率不过就是“一刹那“间的能量！如果能量有函数，那么功率就是能量函数关于时间的导数！这没什么稀奇的。而且对于我们需要模拟的光照来说，E本身就是发光体的能量辐射方程。而一般情况下，这个能量近似都是恒定的，比如太阳辐射、一盏打开的灯光等，所以最终光源的辐射功率其实也就是个常数（基本不随时间变化，或变化很慢，比如中午的太阳照射）。当然因为功率也就是一刹那间的能量，一旦功率确定了，那么在一刹那间的能量也就几乎可以被认为是一个常量值。这也就是我们可以一个固定的RGB值表示光源颜色的意思，也就是说我们所有计算的开始几乎就是个“常量”，这听上去非常棒！或者说RGB颜色就是光源能量的采样值。

5.4、辐射通量密度

  接下来，让我们稍微烧下脑，首先我们想象一下，刚才反复提到的辐射到底是表达个什么意思？比如太阳光，太阳是个巨大的球体，无论其发光能量多大，都是一个有上限的值，而且因为太阳是个巨大的球体，所以这些能量或者说恒河沙数般多的光子都是朝“四面八方”散射出去的，随着光速飞离光源，从太阳表面算起，离太阳表面越远，总能量值是不变的，而光子之间的距离却离得越来越远，这里不要忘记了光是“直线传播”的这一特征。最终当这些光子碰撞到物体，比如地球的时候，单位面积上光子数量是比相同面积的太阳表面上变少了很多的，综合起来，也就是说虽然能量是守恒的，也就是说每个“一刹那”间，太阳向外辐射的总能量是不变的，即辐射功率是不变的，但是最终落到物体表面上的光子却变少了，也就是单位面积上接收的辐射通量（辐射功率）变小了。或者直观的理解，光辐射在一个方向上几乎是以“喇叭形”展开的。

  另外辐射的过程可以想象成一个形象的例子——吹气球，气球在没有吹起膨胀的时候，其厚度是很大的，而且几乎是不透明的，因为球表面的分子是很致密的排列的，当气球被吹起以后，我们会看到当气球膨胀的越大其表面积就越大，那么球体的厚度我们可以明显感觉到变薄了，而且球体开始渐渐有些透明了，这说明单位面积上的分子变少了。这与光从太阳表面辐射出来时的情形很相似。

  怎么去表达这样的变化呢？这时就又需要使用微积分的知识，我们需要知道在一个“无穷小”的表面积上，一刹那间，辐射能量或者说光子是怎样分布的（光子非常非常小，所以即使在一个几乎"无穷小"的面积上仍然可能会有恒河沙数般的光子，可能这已经超出了你的想象力），这就是辐射通量密度：
$$\begin{gathered} 辐射通量密度(单位面积上的辐射通量): \\ D=\frac{d\Phi }{dA} \\ dA表示微面积，单位:瓦/平方米,W\cdot m^{-2} \\ 入射辐射度D，\Phi 为前式中的辐射功率（辐射通量）。 \end{gathered}$$
  看到了这里，聪明的你可能以为这样就能计算了，先不要过渡兴奋，虽然面积很好算，而且光源的功率我们可以假设一个值或者模拟一个随机范围的函数，最终利用RGB表示，仿佛我们就能算出最终某个面积上的辐射度了，那不就是最终某个Mesh表面上的颜色咯？如果你这样想，我只能说你图样图森破了！

  举例来说对于辐射功率恒定的某个半径为r的发光球体来说，其表面上的辐射通量密度为：
$$D_s=\frac{{\Phi }_s}{4\pi r^2}$$
  当然事情还没那么简单！请收起你的“假想”，让我们继续，接着让我们共同来了解一个重要的几何概念——立体角。

5.5、立体角

  一般情况下，我们知道光源都是“球体”，或者近似“球体”，当然在我们实际计算中，我们也会碰到“点光源”、“面光源”、甚至更复杂形状的光源等，但无论什么样的光源，除了激光之外，我们知道光都是呈“锥形”向外散射的。

  这时让我们思考一下，从光源的光发射点算起，这个锥体随着光的传播，散射的面积是不是越来越大？（想象喇叭的形状）而且不同的光源，其形成的散射锥体（喇叭形）是不是也有“大小”不同的区别？那么从平面的角度认识这个问题，等同于说每个锥体的“角度”是不同的。那么也就是说因为初始的角度大小不同，并且光速是恒定的，所以最终离光源相同距离的面积上，被辐射到的光子数量是不一样的。也就是说角度大小也决定了最终表面积上接收到的功率！

  那么把这个问题还原到3D空间中，这个角度怎么表达？这就是我们要说的立体角。

  根据大家从小学到中学期间学的角度的知识，我们知道可以用弧度这种方式，优雅的表达一个角度的大小：

  那么在3D空间中，其实一个“角度”就是一个“尖锥体”（需要注意的是可能不一定就是圆锥），称之为立体角：

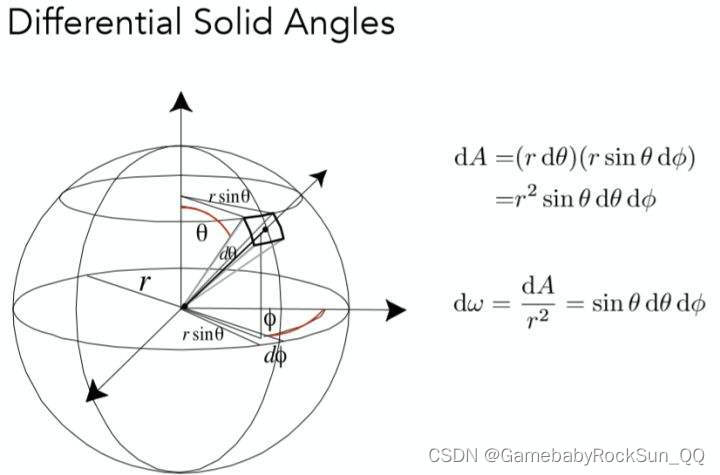
  式中 $d\omega$ 就是立体角，抛开复杂的球坐标系以及微积分符号，那么可以发现其表达式就是面积除以半径的平方，这与平面角度的弧长除以半径，形式上是“一致”的（由此可以推算一下4D空间中的“立体角”又怎么表达？那么思考一下我们人类有没有被类似“二向箔”这样的武器攻击？）。

  也就是说立体角表示一个锥面所围成的空间部分，用符号 $\omega$ 表示。立体角是以圆锥体的顶点为心，半径为r的球面被锥面所截得的面积来度量的，度量单位为“球面度”（steradian，符号∶sr）。球面度表示为三维弧度。

  反过来，可以验证一下，在半径取单位长度的球体上，面积越大，那么立体角就越大。当球体半径越大时，面积相同的时候，那么立体角就越小。那么最终如果立体角相同，半径越大，那么对应的面积也就越大！而这说明立体角正确的表达了3D空间中“角度”的大小，正如弧度正确的表达了平面角度大小一样。它是3D空间中角度大小的“不变量”，也既如果立体角给定，无论球体半径大小如何变化，那么最终面积也随之变化，而“角度”始终不变。

  如果你彻底理解了立体角的含义，那么应该可以立即想到，整个球面立体角的大小是 $4\pi$ ,而半球的立体角是 $2\pi$。至于这是为啥，我想不用再多说了，聪明的你一应该一下就想到了。而这里扩展提醒你的是说，当你看别的PBR材料时，当其中总是会莫名其妙出现 $4\pi 、2\pi 、\pi$ 时，应该立刻联想到球面的立体角，而不是角度！

  到此，回到前面的问题，我们就知道，从光源点算起，光散射的锥体的大小就可以用“立体角”正确的表达！也就是说立体角越大，光能量散射的越快，相同距离上相同面积下得到的辐射功率也就越小！那么也就是说，立体角的大小与最终表面上获得的辐射能量成反比！

  这里提示一下，在传统光照模型改进版中，有个光线衰减因子，通常是与距离平方成反比的，根据这里的知识，想想是为什么？

5.6、辐射度

  有了上面的知识，那么我们就要引入一个重要的概念，辐射度，即在单位立体角及单位面积上辐射出的功率（辐射通量）。表达如下：
$$\begin{gathered} 辐射度L定义每单位立体角、每单位投影面积上的辐射通量（辐射功率）。 \\ 辐照度表示空间内任一点处、某一方向上的辐射通量， \\ 并计算垂直于当前方向虚拟表面上的、每单位面积内的辐射通量。 \\ 单位同辐射强度W\cdot m^{-2}\cdot s{r}^{-1} \\ L=\frac{d^2\Phi }{d{A}^{\perp }d\omega } \\ 式中sr是立体角的大小，类似于平面角的“弧度”，是个无量纲的量， \\ 这里之所以强制定义了一个单位，是为了跟单位面积上的辐射通量相区别。 \\ d{A}^{\perp }表示与辐射方向（也就是光线方向）垂直的微面积。 \end{gathered}$$
  上式是微分表达式，当式中 $d\omega \to 0,d{A}^{\perp }\to 0$ 时，其整体就退化为一个点，而 $d\omega$ 就退化为一个向量（也就是传说中的“光线”）。记住这点很重要，因为后续的计算我们就是把它当做一个方向向量。这种微分近似其实也是有自然意义的，因为一般情况下我们都将光称之为光线，当光锥无限细分下去之后，光真的就退化还原为一条条近似无限长的细线，所以一条条光线计算明白了，那么最终通过积分，总体的光辐射的能量也就计算明白了。

  从上式我们还可以看出以下几点：

（1）、当光线穿越空间时，辐射度在该光线方向上可以看做一个“恒定量”，也可以理解为一个个等能量的光子组成的一根“线”，或者直接理解为一个小小的“光子”的飞行轨迹。而且在两个方向上都是恒定的（理解这点很重要！希望我讲明白了，实质是说光的传播是有方向的，而空间是各向同性的，当然部分晶体内部除外。）；

（2）、因为辐照度最终整体退化表达一个点上接收或发射的单位功率的大小，所以它几乎可以作为我们所有光照模型中最微小和基本的一个单元，比如一个像素上接收某个光源辐射过来的光能量，或者某个光源上某点朝某个方向辐射出的光能量等等；

（3）、微观上空间中某点的辐射度确定了之后，就不用再理会它是入射的光还是出射的光等；（这与第一条类似，但是理解的角度不同，这也对我们后续的计算有莫大的帮助。）

  一般的，我们将物体表面微元上接收到的辐射度称之为入射光，而从微元上射出（反射、折射、散射等）的辐射度称之为出射光，注意出射光可能是反射光也可能是散射光，甚至可能是折射光，这些我们可以统称为出射光，而面积微元可以直接理解为“点”（不能理解为数学上的点，更确切的说应当理解为一个像素、纹素等）。

  对于剩下的 $d{A}^{\perp }$ 其实它是指最终表面一定要垂直于光线的方向，无论入射还是出射，一般情况下，很难遇到光线恰巧与表面垂直，他们之间必定存在一定夹角 $\theta$，此时有：
$$\begin{gathered} Lambert定律：入射辐照度正比于入射角。 \\ d{A}^{\perp }=\cos \theta dA \\ L=\frac{d^2\Phi }{dA\cos \theta d\omega } \\ \cos \theta d\omega 称作投影立体角 \\ 当光线方向确定的情况下，此时\cos \theta =\vec{n}\cdot \vec{\omega } \\ 其中\vec{n}为A的法线，\vec{\omega }为光线的方向(立体角的轴线方向) \end{gathered}$$
  实际上式中 $L$ 的微分表达指的就是一条光线穿过空间中一点时的辐射通量。入射光角度与面积投影角度的关系如下图所示：

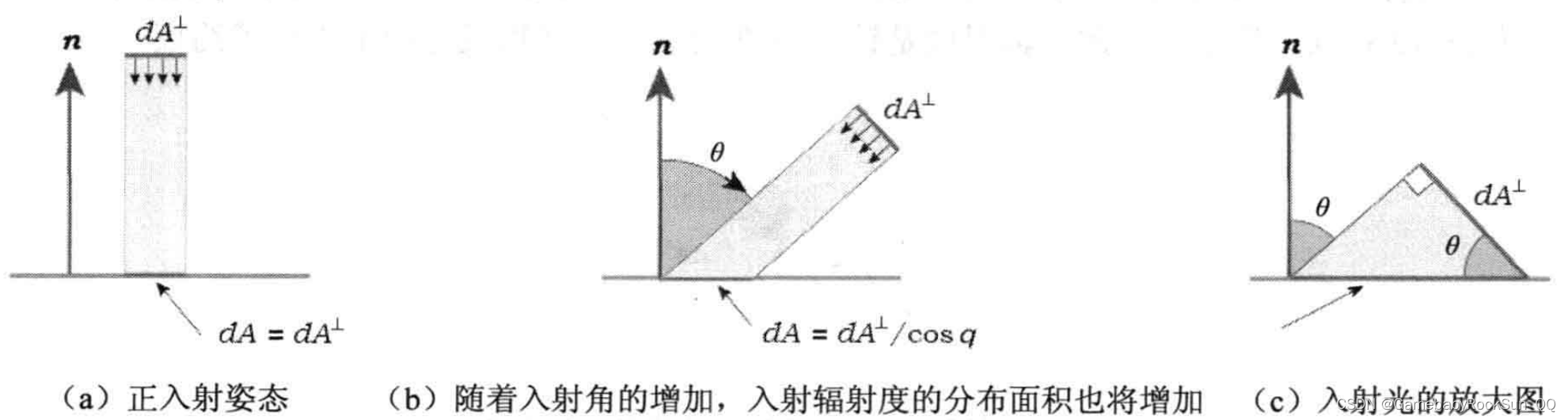
  需要注意的就是，$\theta$ 一般位于表面法线与光线“之间”（有可能同侧也可能不同侧！想想为啥？）

  对于一个半径为r的恒定辐射功率为 ${\Phi }_s$ 发光球体来说，其表面的辐射度为：
$$L_s=\frac{\Phi }{4\pi r^2\cdot \frac{1}{4\pi }}=\frac{\Phi }{r^2}$$
  上面的结果很有意思，想想为啥？这个式子在本章示例的Shader代码中也有体现，后面还会讲解。

5.7、辐照度方程

  搞明白了辐照度方程，那么就先来研究一下在入射光时，方程是怎样的，根据前面的推导有：
$$\begin{gathered} \because D=\frac{d\Phi }{dA} \\ L=\frac{d^2\Phi }{dA\cos \theta d\omega }\Rightarrow \frac{d^2\Phi }{dA}=L\cos \theta d\omega \\ \therefore d{D}_i(p,{\omega }_i)=L_i(p,{\omega }_i)\cos {\theta }_{i}d{\omega }_i \\ 式中D_i表示入射辐照度，i是input的缩写，p为入射点，{\theta }_i为入射角，{\omega }_i为入射方向 \\ 此处式中D和L都是点p和{\omega }_i的函数 \end{gathered}$$
  因为我们本身就考虑的是“瞬时”能量，即功率的关系，所以时间t参数可以忽略，只需要求出辐射通量（辐射功率）的关系即可。

  有了关于点p的辐射度的微分方程（一条光线），那么根据入射点p关于所有入射辐照度（所有入射向量组成的立体角）求积分（注意是向量积分，跟普通积分略有区别），因为不止一条光线照射进p点，实质在以p点为球心的半球，有时候甚至是球体中，会有四面八方射入的光线（多条光线），就可得出p点上收到的全部入射辐照度，即：
$$D_i(p)={\int }_{{\Omega }_i}{L}_i(p,{\omega }_i)\cos {\theta }_{i}d{\omega }_i$$
  对于计算来说，根据我们之前说的 $d\omega$ 的极限就是一根线，在这里就是入射光的矢量，如果光源位置确定，那么其实 $d\omega$ 就是点 p 减去 光源点位置矢量后的差矢量。所以 $d\omega$ 与点p及光源位置都有关系，而 $\Omega 就是包围p点的空间，对反射光来说一般是半球$，其实这个积分就是说求出围绕p点的半球立体角内射入的所有功率。最后需要注意的就是因为角度和立体角单位都是无量纲量（注意弧度、sr等单位都是被强制加上的，只是为了与普通的数字相区分），所以最终 D 和 L 的单位相同，即我们计算出来的其实都是某点处的辐射功率密度（想想为啥只是辐射功率密度？还需不需要对面积做积分？）。

  同时思考下，既然 $d\omega$ 与点p及光源位置都有关系，想象一下现实中不止有光源，还有来自环境中的各种复杂的环境光，如反光、散射光等等，这时这个计算量会有多大？（注意这里实质上是个球面积分或半球面积分，如果考虑精度要求的话，积分项必须要足够多和足够细粒度）这还只是计算一个点p上的入射辐照度！当我们至少需要计算屏幕空间大小面积中的每个点上的入射辐照度时，计算量将更是非常巨大的！

  而这与传统光照中，只考虑从光源到点p上的一条矢量，然后乘以某个系数，比如反光系数（传统光照中往往就是视向量与反射光线矢量之间的点积），得出最终光照的计算来说，其增加的计算量是几何级数倍的。当然现在不用过度担心这个计算量爆炸的问题，因为很多前辈大佬已经帮我们想出了很多相当棒的方法来高效的实现这个计算过程（实际上很多是最终渲染质量与计算效率间的折中方法），我们所要做的就是站到巨人的肩膀上！

  看到这里，各种微积分应该让数学功底不太好的同学们有点发晕了，那么让我们换换脑筋。各位应该听说过“戴森球”吧？就是传说中，宇宙高等文明为了获取一颗恒星全部的能量，就会建造一个巨大的球壳体，把整个恒星包起来，此时所有的恒星出射能量都会被这个球壳体以最大的形式吸收，这时我们可以根据前面这个积分方程简单估算一下为什么会这样？在“戴森球”中，我们可以看出积分的 $\Omega$ 就是整个球壳体，这时 $\int d\omega =4\pi ，\theta =0，\cos \theta =1，{\Omega }_A=4\pi r^2$，又因为L根据定义在“戴森球”的情况下需要除以整个球面的立体角 $4\pi$ 以及整个球壳的表面积，所以对立体角即面积积分后这些常量项都“相互抵消”了，所以最终所有恒星辐射出的能量，就都被“戴森球”给吸收了，也就是说 $D=\Phi$，相当于“戴森球”吸收了恒星辐射出的所有“功率”，假设恒星辐射功率恒定，此时如果继续再乘以时间，就可以知道“戴森球”吸收了多少能量。

  OK，至此你已经掌握了我们这个宇宙中高等级文明通过“戴森球”获取全部恒星能量的秘密！所以请相信光！

5.8、可见光谱辐照度

  如果要考虑光源的波长特性，也就是颜色特性，或者直白的说是量子特性时，对于可见光范围来说，我们有下式：
$$\begin{gathered} L_i(p,{\omega }_i)={\int }_{390nm}^{700nm}{L}_{\lambda }(p,{\omega }_i,\lambda )d\lambda \\ {L}_{\lambda }单位:W\cdot m^{-2}\cdot s{r}^{-1}\cdot n{m}^{-1} \end{gathered}$$
  注意式中被积分的函数 $L_{\lambda }$ 是一个关于点 $位置向量p、光线方向向量{\omega }_i以及光波长\lambda$ 的函数，积分的意思是说关于所有可见光波长积分就得到了复合光线中所有波长的辐照度，积分后波长参数就消失了。

  其实这个式子是实时PBR与非实时的真实PBR的第一个分水岭，非实时电影级画质PBR中，对于每种光源必须要测量出类似前面展示的太阳的SPD辐照度波长函数图形，然后数值积分得到光源的真实辐照度，再进行后续的计算，如果场景中光源比较丰富复杂时，大家可以自行脑补下这个计算量的大小。

  而在实时近似的PBR中，最终 $L_i$ 简化为RGB分量来表示辐照度的近似采样值，当然方向以及光源位置需要别的参量来表示或计算。

  在本章示例代码18-PBR-Base-Point-Lights 中，我们取了一些固定值：

pstCBLights->m_v4LightClr[0] = { 23.47f,21.31f,20.79f, 1.0f };
pstCBLights->m_v4LightClr[1] = { 53.47f,41.31f,40.79f, 1.0f };
pstCBLights->m_v4LightClr[2] = { 23.47f,21.31f,20.79f, 1.0f };
pstCBLights->m_v4LightClr[3] = { 23.47f,21.31f,20.79f, 1.0f };

  需要注意的是，上面这些光源点的颜色值(辐照度值)都是远远超过0.0f~1.0f的值，并且是RGBA形式表达，alpha通道的意义只是为了4个float字节大小边界对齐而特意加的，计算中基本被忽略了，这样做的意义只是为了性能。而示例中之所以这样表达是因为，物理世界中的光照能量值是远远超过计算机中所能表现的范围的（更主要的原因是计算机中最终表达的往往是反射、折射或散射后的光能量，已经大大衰减了，而很少直接表示光源。最直观的理解就是计算机屏幕即使调到最亮，也不能当灯泡来使用。）所以为了能够表达这种真实世界中光照能量的巨大范围，我们就必须设定光源的RGB分量是个巨大的值（HDR）。

  另外，本章例子为了讲清楚PBR的基本计算，只是使用了几个点光源，而在更真实的PBR渲染中，这就远远不够了，因为在真实世界中，物体所能受到的光照来源是很丰富的，除了常见的阳光，还有来自于天空的散射光，来自场景中其它物体的反射光、各种漫射光等等，这种复杂的情形下，一个或几个小小的点光源就不够表达了，此时需要一种称之为HDR环境光映射的图片来表达了，HDR我们会在后续简单介绍。所谓环境光映射，现在可以简单的理解为就是一个天空盒子图片，只是它里面存储的是光源以及各种反射散射等的光源的颜色信息，即整个环境中光能量的信息，这个我们后续教程中还会更详细的介绍。

  基于RGB颜色值是辐照度的离散采样值的认识，可以反过来理解，也就是说RGB信息中包含了能量、波长的信息，本质上就是针对波的采样，基于此，所以很多算法可以对图片进行FFT变换等操作，来抽取图片中的频域信息，或者对图片进行梯度计算等，这也是很多图形算法行之有效的基础前提。

  这里还需要注意的是，在PBR中，一般讲到光源的时候，不能再简单的理解为是某个发光体，比如太阳，而是说几乎所有的能反射光或折射散射光的场景物体都需要被当做光源看待。也就是说一个物体的出射光可能就是另一个物体的入射光。这个很好理解，想象一辆漆刷的很亮的汽车表面，总能映照出周围环境的影子，就是个很好的例子。

5.9、入射辐照度与出射辐照度关系

  看到这个小节的标题，大家不要被吓到，其实这里说的就是入射光与出射光（反射光、散射光等的统称）之间的能量关系。在几何光学中，表达的则是入射光和出射光，比如入射光与反射光、折射光等的几何关系，也就是角度关系，而有趣的是，其实除了激光以及一些特殊情况之外，我们其实几乎就没有见过光线本身以及这些光线间的角度关系，我们始终看到的都是颜色，也就是光的能量，而我们先理解到的居然是光的角度关系。

  根据我们平时的一些小常识，可以立即知道，出射的辐照度与入射的辐照度除了简单的几何关系外，另一方面就是在二者能量关系上是成比例的关系，即出射辐照度一定正比于入射辐照度。
$$\begin{gathered} d{L}_o(p,{\omega }_o)\propto d{D}_i(p,{\omega }_i) \\ 式中L_o为出射辐射度，这与之前的L_i定义类似，只是方向不同 \end{gathered}$$
  如果是两个简单的变量成正比关系，那么我们可以简单的写成 $y=kx$ 的形式，但是对于这两个函数来说，其“线性比例系数”就不能是常数系数了，而是一个函数系数，这就是著名的BRDF函数。

5.10、BRDF

  根据教科书上的定义，BRDF即双向反射分布函数(Bidirectional Reflectance Distribution Function,BRDF)是用来定义给定入射方向上的辐射照度如何影响给定出射方向上的辐射率。

  其实本质上来说，BRDF其实就是个“函数比例系数”。相对于常数比例系数“k”来说，还有一大类经常碰到的比例系数就是矩阵。这些比例系数都从形式上表达了最最基本的“线性”关系：$y=kx$ !，这就需要分别看$x,y$ 代表的是什么量，若为普通一元变量，那么k就是常数，若表达的是向量，那么k就是矩阵，若表达的是函数，那么 k 对应的就是函数，一般情况下系数函数需要在一定范围内是个单调函数，也就是说随着x的增大，y也对应比例的增大或缩小，不然也就不能称之为比例系数了。

  对于我们讨论的入射辐照度以及出射辐照度来说，假设这个“函数比例系数”为f，则有：
$$\begin{gathered} \because d{L}_o(p,{\omega }_o)\propto d{D}_i(p,{\omega }_i) \\ d{L}_o(p,{\omega }_o)=f_r(p,{\omega }_i,{\omega }_o)d{D}_i(p,{\omega }_i) \\ \because d{D}_i(p,{\omega }_i)=L_i(p,{\omega }_i)\cos {\theta }_{i}d{\omega }_i \\ \therefore d{L}_o(p,{\omega }_o)=f_r(p,{\omega }_i,{\omega }_o)L_i(p,{\omega }_i)\cos {\theta }_{i}d{\omega }_i \\ {f}_r(p,{\omega }_i,{\omega }_o)=\frac{d{L}_o(p,{\omega }_o)}{L_i(p,{\omega }_i)\cos {\theta }_{i}d{\omega }_i} \\ 因此BRDF即f_r单位为s{r}^{-1}。 \\ BRDF仅为点p及两个方向向量上的函数，所以其值域为0\sim \infty \end{gathered}$$

  式中需要注意，之所以出射辐照度是微分，是因为对于点p的每一条出射光线来说，所有的入射辐照度都会对它产生影响，所以出射辐射度就是微分形式，即某点的某方向上的出射光线的辐射度中受到某个入射光的影响的那一小部分。另外当BRDF趋近于无穷大时是说产生的是完全镜面反射了，可以参考下光纤中光线传播的情况。

  对于BRDF来说，它有几个特征：

（1）、即双向特征，也称为交换特征，也就是对于所有的 ${\omega }_i和{\omega }_o$ 来说，交换这两个方向，BRDF是保持不变的。也既：
$$f_r(p,{\omega }_i,{\omega }_o)=f_r(p,{\omega }_o,{\omega }_i)$$
（2）、线性特征，这个在前面已经形象的说过了，因为BRDF归根结底就是个“比例系数”，根本上表达的就是线性关系。当然这是一般情况下，我们碰到的材料都是线性反射光线的而已，对于非线性光学来说不是这样的，比如激光在激发的时候。当然线性的另一层含义是说，这个比例系数还遵循下面的线性关系：
$$\begin{gathered} f(kx)=kf(x) \\ f(k_{1}x+k_{2}x)=k_{1}f(x)+k_{2}f(x) \end{gathered}$$
  当然这个关系看着有点晕，其实它就是说，如果入射辐照度变强了几倍，那么出射辐照度就会变强几倍，而且对于多个光源来说最终的出射能量是可以简单线性相加的。这也符合我们对光能量的感知。这也是说，在实际的计算中，材质表面某点的多个BRDF特征是可以进行线性叠加得到最终结果的。

（3）、BRDF是遵循能量守恒的，这个就不多说明了，后面的推导中将更清晰严格的表达这个含义。

5.11 反射辐照度

  对于实际的光照来说，最重要的出射辐照度就是反射辐照度，按照不装13的说法，其实就是说对于光的传播过程来说，反射光是最重要的一类出射光（另一大类是透射光，二者主要的区别就是透射光穿过了物体表面，而反射光只在物体表面发生），所以我们有必要先研究下反射光的方程。对于反射光来说，只需要对某点所有入射光引发的反射光线的辐照度进行积分即可（实际还是立体角积分），也就是说：
$$\begin{gathered} {\mathrm{L}}_o(\vec{p},\overrightarrow{{\omega }_o})={\int }_{{\Omega }_i}{f}_r(\vec{p},\overrightarrow{{\omega }_i},\overrightarrow{{\omega }_o}){\mathrm{L}}_i(\vec{p},\overrightarrow{{\omega }_i})\cos {\theta }_{i}d\overrightarrow{{\omega }_i} \\ 一般对点p上方正半球（立体角）积分， \\ (因为反射就是在表面与入射光同侧发生的，对于散射光来说不是这样)： \\ {\mathrm{L}}_o(\vec{p},\overrightarrow{{\omega }_o})={\int }_{{2\pi }^{+}}{f}_r(\vec{p},\overrightarrow{{\omega }_i},\overrightarrow{{\omega }_o}){\mathrm{L}}_i(\vec{p},\overrightarrow{{\omega }_i})\cos {\theta }_{i}d\overrightarrow{{\omega }_i} \\ \because \vec{n}\cdot {\omega }_i=\cos {\theta }_i \\ \therefore {\mathrm{L}}_o(\vec{p},\overrightarrow{{\omega }_o})={\int }_{{2\pi }^{+}}{f}_r(\vec{p},\overrightarrow{{\omega }_i},\overrightarrow{{\omega }_o}){\mathrm{L}}_i(\vec{p},\overrightarrow{{\omega }_i})\vec{n}\cdot {\omega }_{i}d\overrightarrow{{\omega }_i} \end{gathered}$$
  这个方程只是说对于反射光来说，基于某个微表面上的点p的正半球做个立体角的积分,注意 $2{\pi }^{+}$ 的含义，那么按照常识我们立即就知道所谓正半球就是说光线入射的那一侧，而 $\vec{n}$ 就是微表面上的法线。同时需要注意的是为了让大家准确掌握这个积分式的含义，特意加入了向量的表达，也是提醒大家一定要知道这一系列的计算其实都是向量计算！同时这个方程说明对于所有的入射光 $\int d{\omega }_i$ 来说，都会对一个特定方向 ${\omega }_o$ 上的反射辐照度产生贡献（这与传统光照模型中的观点是有极大区别的）。

  另外在一些其它的PBR资料中，所有的后续推导都是从这个方程开始的,，并且有些材料或教程中将其称之为反射率方程，其实这还不是反射率，正确称谓应该是反射方程，后面会继续介绍反射率。同时我相信你现在不应该再对这个方程有所畏惧或者一无所知了，觉得这是多么高深的一个开始，我相信怎么推导它你已经很清楚了，你也一定清楚了它所表达的物理含义：就是所有照射入p点的光线，都会对某个特定方向的反射光线产生贡献，通常这个特定的方向就是虚拟摄像机到p点的方向，也就是常说的“视方向”矢量，而这里所有的过程都是“线性”的。实际计算中，这里所说的“所有照射入p点的光线”往往就是整个环境中产生的直接照射或间接照射。

  从这个相对复杂的积分过程，反过来回顾下传统光照中关于反射光线计算的处理，其实都是这个方程的极简特例，即使用从光源到点p的一条矢量作为入射光方向，然后根据表面上的法线计算出反射光的方向，然后再由反射光方向与眼睛到点p的矢量做点积作为最终看到的颜色的一个系数，传统光照中管这个叫“镜面反射”，整个过程对于任何点来说几乎都是固定量的一个计算，所以计算速度很快，但准确度上只能理解为是个“平均水平”的近似。

5.12、BSDF

  上述的BRDF以及反射方程，基本就概括描述了之前介绍的反射光的部分，而对于透射的散射光来说，散射方程的推导过程以及形式与反射方程式类似的，只是其中比例系数函数就不再叫做BRDF了，而是称之为BSDF（双向散射分布函数 Bidirectional Scattering Distribution Function）。一般情况下，BSDF包含了BRDF（反射部分）和BTDF（透射），也就是即考虑反射部分还要考虑光穿透介质形成的透射部分，因为需要考虑能量守恒，所以就需要两部分来计算各自占据入射光能量的分配比例。对应的还有BDDF（衍射），BSSRDF（双向表面散射反射分布函数）。其中BSSRDF是最全面描述出射辐照度与入射辐照度之间比例性质的函数。

  因此一般光线照到物体表面后，能量通常会分成五个部分：镜面反射、漫反射、折射、散射、吸收。通常的渲染中，对于一些非透明的物体，只需要考虑镜面反射和漫反射即可，也既对非透明物体，尤其是金属材质表面物体只需要考虑BRDF即可，这基本可以处理场景中几乎80%的物体了（当然如果某个场景中几乎都是透明、半透明或高散射的物体时，第一你要注意你的显卡，第二这很可能是个为了炫耀渲染特效的demo，或者干脆就是作者在装13，当你真的我看到时，那就果断点赞吧:-）。

  在一些材料中，将上述比例函数统称为BxDF，类似于线性代数中将所有的比例系数统称为矩阵一样，对应的BRDF、BSDF等都是BxDF的特例。总之无论其称谓如何，都应了解BxDF的本质就是表达出射辐照度（某种、某几种或全部）与入射辐照度之间比例关系的系数函数而已！

5.13、反射率

  根据前面的推导，已经得到了反射辐照度，并且大家要注意的是反射辐照度只是出射辐照度中的一种而已，对于其它的出射辐照度，还必须要倒回到BRDF的基本方程来推导，这也是将来大家继续深入学习PBR时，需要注意的一个特点。

  而大多数其它的PBR教程都是从反射辐照度方程开始的，然后推导出了后面要讲到到的“金属工作流”的近似反射方程后就结束了，其实这只是PBR渲染中的一个分支而已。所以要全面掌握BxDF就需要完全掌握BxDF方程的原理和推导，实际中很多论文都是从推导某种光照场景下材质表面的BxDF函数的构造，再进行模拟计算，然后渲染出效果，最终与真实情况下进行比较而产出的。所以我这里就从一开始给大家完整讲下原理，方便大家真正掌握这个基础后，去全面掌握PBR渲染（甚至非实时的PBR渲染也是从BxDF开始的）。

  再继续之前，有必要进一步继续学习下基础中较深入的部分。首先让我们来看看什么是真正的“反射率”。

  从纯物理的意义上来讲，反射率其实指的应该是“功率”转换的比率，类似于计算热机的机械效率一样。而根据前面的推导，反射辐照度方程其实表达的是功率密度关系的方程，不是关于功率的方程，还需要进行一次关于“面积”的积分，那么根据前面的方程，可以有下面这些公式（注意下面dA的写法不是很严谨，只是为了方便，我相信你一定知道严谨的写法应该是怎样的）：
$$\begin{gathered} 入射辐射通量（功率）： \\ d{\Phi }_i=dA{\int }_{{\Omega }_i}{L}_i(p,{\omega }_i)\cos {\theta }_{i}d{\omega }_i \\ 出射辐射通量（功率）： \\ d{\Phi }_o=dA{\int }_{{\Omega }_o}{L}_o(p,{\omega }_o)\cos {\theta }_{o}d{\omega }_o \\ 根据刚才推导出的反射辐照度方程： \\ {\mathrm{L}}_o(\vec{p},\overrightarrow{{\omega }_o})={\int }_{{\Omega }_i}{f}_r(\vec{p},\overrightarrow{{\omega }_i},\overrightarrow{{\omega }_o}){\mathrm{L}}_i(\vec{p},\overrightarrow{{\omega }_i})\cos {\theta }_{i}d\overrightarrow{{\omega }_i} \\ 代入得到所有反射通量与入射通量的关系： \\ d{\Phi }_o=dA{\int }_{{\Omega }_o}{\int }_{{\Omega }_i}{f}_r(\vec{p},\overrightarrow{{\omega }_i},\overrightarrow{{\omega }_o}){\mathrm{L}}_i(\vec{p},\overrightarrow{{\omega }_i})\cos {\theta }_i\cos {\theta }_{o}d\overrightarrow{{\omega }_i}d\overrightarrow{{\omega }_o} \\ 根据反射率的定义，对两个通量取比值得反射率\rho （此时dA约分消除了）： \\ \rho (p,{\Omega }_i,{\Omega }_o)=\frac{d{\Phi }_o}{d{\Phi }_i}=\frac{{\int }_{{\Omega }_o}{\int }_{{\Omega }_i}{f}_r(\vec{p},\overrightarrow{{\omega }_i},\overrightarrow{{\omega }_o}){\mathrm{L}}_i(\vec{p},\overrightarrow{{\omega }_i})\cos {\theta }_i\cos {\theta }_{o}d\overrightarrow{{\omega }_i}d\overrightarrow{{\omega }_o}}{{\int }_{{\Omega }_i}{L}_i(p,{\omega }_i)\cos {\theta }_{i}d{\omega }_i} \end{gathered}$$
  上面的推导过程看上去有点复杂，其实最终无非就是根据入射立体角和出射立体角对辐照度进行积分，从而得到所有的入射辐射通量密度（入射功率）以及所有的反射辐射通量密度（反射功率），最终取比值就得到了反射率（注意不需要对面积积分，计算一点的所有入射和出射光即可，即使对面积积分了，因为最后是取比值，所以相关面积因子也就抵消了。当然对于复杂表面来说，反射率可能是表面上点p的函数，即每点的反射率不同，后面讲漫反射的时候大家就更能理解这是什么意思了。对应的大家可以思考下散射率、折射率等应该怎么计算）。

  根据物理常识，我们知道，首先一般情况下不可能有理想的完全反射光线或者能量的表面介质，比如镜子也不是严格完全反射的（光跨介质的全反射是特例，但任然有能量损耗，所以光纤的传输距离也不是真正“无限”的）；其次，并不是所有的入射光都被完全反射出去了，有些可能被介质表面吸收了，有些是吸收后散射了等，还有些可能是折射出去了，所以从能量的角度讲，并不是所有能量都被反弹出来；再次、光本质上作为能量一定是遵循能量守恒定律的。

  所以最终就可以知道，反射率取值范围为：
$$0<\rho (p,2{\pi }^{+},2{\pi }^{+})<1$$
  也就是说无论对什么样的材质表面反射功率始终是小于入射功率的。同理可以立刻知道，折射光、散射光等都应当是小于入射总功率的。

5.14、完全漫反射BRDF（Lambertian反射）

  利用基本的反射方程，可以得到一个理想情况下的反射方程，被称之为完全漫反射,也被称之为Lambertian反射。这种场景是说，所有的入射光线被均匀的从p点正半球均匀分布反射出去了，并且所有的反射都是完全漫反射，可以直观的理解为在半球中光线被均匀的反射出去了，这时入射光方向与出射光方向都不影响这个反射的过程。

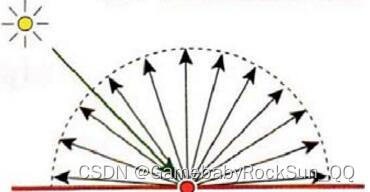
  此时BRDF函数与 ${\omega }_i,{\omega }_o$ 都没有关系，也既不是二者的函数，推导如下：
$$\begin{gathered} \because {\mathrm{L}}_o(\vec{p},\overrightarrow{{\omega }_o})={\int }_{{\Omega }_i}{f}_r(\vec{p},\overrightarrow{{\omega }_i},\overrightarrow{{\omega }_o}){\mathrm{L}}_i(\vec{p},\overrightarrow{{\omega }_i})\cos {\theta }_{i}d\overrightarrow{{\omega }_i} \\ 根据假设有：f_r(\vec{p},\overrightarrow{{\omega }_i},\overrightarrow{{\omega }_o})=f_r(\vec{p}) \\ \therefore L_o(\vec{p})=f_r(\vec{p}){\int }_{{\Omega }_i}{L}_i(\vec{p},\overrightarrow{{\omega }_i})\cos {\theta }_{i}d\overrightarrow{{\omega }_i}=f_r(\vec{p})D_i(\vec{p}) \\ {f}_r(\vec{p})=\frac{L_o(\vec{p})}{D_i(\vec{p})} \end{gathered}$$
  上式中最后的BRDF函数 $f_r$ 只与每个点p自身的属性有关系，而与入射光的方向以及出射光的方向都无关，即 $f_r$ 是个关于点p位置的函数。

  接着我们来看下这个过程的实际反射率：
$$\begin{gathered} d{\Phi }_o=dA{L}_o(\vec{p}){\int }_{2{\pi }^{+}}\cos {\theta }_{o}d{\omega }_o=dA{L}_o(\vec{p})\pi \\ 注意上式中的积分项：{\int }_{2{\pi }^{+}}\cos {\theta }_{o}d{\omega }_o，想想怎么推导和积分？即为啥它=\pi ? \\ 提示：\cos {\theta }_o=\vec{n}\cdot \overrightarrow{{\omega }_o}然后转换到球坐标系 \\ d{\Phi }_i=dA{\int }_{2{\pi }^{+}}{\mathrm{L}}_i(\vec{p},\overrightarrow{{\omega }_i})\cos {\theta }_{i}d{\omega }_i=dA{E}_i(\vec{p}) \\ {\rho }_d(\vec{p})=\frac{d{\Phi }_o}{d{\Phi }_i}=\frac{\pi L_o(\vec{p})}{E_i(\vec{p})}=\pi f_r(\vec{p}) \\ {f}_r(\vec{p})=\frac{{\rho }_d(\vec{p})}{\pi } \end{gathered}$$
  对于完全漫反射环境光来说，入射辐射度与方向、位置无关，此时用双半球反射系数 ${\rho }_{hh}$ 来表示反射率，注意式中实质上是对两个半球立体角进行了积分。这时若入射辐照度：$Li(p,{\omega }_i)=L_i$ 为常量，有：
$${\rho }_{hh}(\vec{p})=\frac{f_r(\vec{p})}{\pi }{\int }_{2{\pi }^{+}}{\int }_{2{\pi }^{+}}\cos {\theta }_i\cos {\theta }_{o}d\overrightarrow{{\omega }_i}d\overrightarrow{{\omega }_o}=\pi f_r(\vec{p})={\rho }_d(\vec{p})$$
  实时的PBR计算中，对于一般的材质来说，表面出射光主要是漫反射光（不考虑方向）和镜面反射光（考虑方向）组成，而这里推导出的完全漫反射光也就被当做其中的漫反射部分，只是实际应用中考虑到能量守恒还需要再乘以一个比例系数，最终合成：
$$\begin{gathered} f_r=k_d{f}_{lambert}+k_s{f}_{specular-reflection} \\ 式中：k_d+k_s⩽1 \end{gathered}$$
  而根据前面的推导，就可以知道：
$$f_{lambert}=\frac{{\rho }_d(p)}{\pi }=\frac{{\rho }_{hh}(p)}{\pi }$$
  而进一步的，在实时PBR中 ${\rho }_d(\vec{p})$ 就是表面纹理上对应纹素的颜色。所以一般PBR的纹理是需要去掉镜面光，环境光等其它要素后得到的漫反射纹理。不去除的话，根据刚才的BRDF函数可以知道，最终因为纹理上可能已经包含了镜面光能量信息，所以导致再次用镜面反射进行计算后，出现出射能量过大的能量不守恒的效果，最终导致看上去渲染画面过于明亮而失真。比如下面这幅图就是漫反射纹理：

  注意观察其中颜色亮度表现的很“均匀”，几乎看不出任何“光照”的痕迹。现代有很多图片处理工具可以从一副普通的照片生成只包含漫反射部分能量信息的漫反射纹理，甚至一些游戏引擎的材质编辑工具中也带有生成漫反射纹理的功能。其基本原理就是根据我们之前讲的，将图片中像素RGB的信息当做光能的信息，然后使用FFT这样的算法，分析出频域的信息，因为能量和波长以及频率可以简单换算，或者说他们是线性关系，所以最终将高频部分也就是高能量的部分去掉，只留下频率在一定范围内的RGB值即可，其中相对高能部分实际也就是反射光比较多的地方，往往就是过多的包含了镜面反射光的地方，把这部分去掉，基本就可以保证整个图片中最终记录的都是漫反射光了。这也是很多PBR中有些参数特意叫漫反射纹素等的根本原因。另外现代很多摄影摄像器材中大多已经内置了直接拍摄漫反射纹理的功能，可以直接从环境中拍摄高质量的漫反射纹理图片。甚至通常的场景下我们谈论纹理时就是特指漫反射纹理！