过拟合以及正则化（L0,L1,L2范数）

在机器学习中，今天接触模型的正则化，很多问题不是很理解，看了大神的博客http://blog.csdn.net/zouxy09/article/details/24971995，和一些自己的理解写了这篇文章。这篇文章主要回答了，什么是范数，过拟合的原因和情况，正则化为什么可以防止过拟合，L1,L2在解决过拟合中的不同点。

一、范数的定义：
范数是具有“长度”概念的函数。在向量空间内，为所有的向量的赋予非零的增长度或者大小。不同的范数，所求的向量的长度或者大小是不同的。

举个例子，2维空间中，向量(3,4)的长度是5，那么5就是这个向量的一个范数的值，更确切的说，是欧式范数或者L2范数的值。

对于p-范数，如果

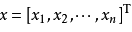
那么向量x的p-范数就是

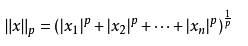
L1范数：

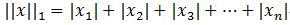
L2范数：

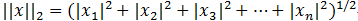
特别的，L0范数：指向量中非零元素的个数。无穷范数：指向量中所有元素的最大绝对值。

二、过拟合：
-对机器学习有一定了解的人相信对过拟合都很熟悉，简单的说就是：对训练集合拟合‘太好了’，而缺对测试集合的泛化性。
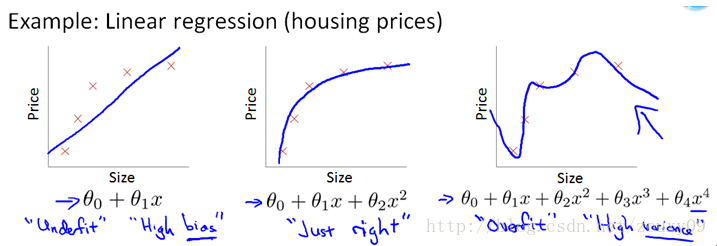
-产生过拟合的原因一般是：模型太复杂，特征选的太多了而测试数据很少。（如图所示）

三，正则化：这里我对大神的总结很膜拜
1,总结一：正则化就是通过对我们的参数进行约束，而使我们的模型更加的简单，使我们对训练集合的拟合更加的平滑。

2，总结二：数学公式：一般来说，监督学习可以看做最小化下面的目标函数：

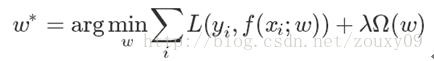
其中，第一项L(yi,f(xi;w)) 衡量我们的模型（分类或者回归）对第i个样本的预测值f(xi;w)和真实的标签yi之前的误差。因为我们的模型是要拟合我们的训练样本的嘛，所以我们要求这一项最小，也就是要求我们的模型尽量的拟合我们的训练数据。但正如上面说言，我们不仅要保证训练误差最小，我们更希望我们的模型测试误差小，所以我们需要加上第二项，也就是对参数w的规则化函数Ω(w)去约束我们的模型尽量的简单。

OK，到这里，如果你在机器学习浴血奋战多年，你会发现，哎哟哟，机器学习的大部分带参模型都和这个不但形似，而且神似。是的，其实大部分无非就是变换这两项而已。对于第一项Loss函数，如果是Square loss，那就是最小二乘了；如果是Hinge Loss，那就是著名的SVM了；如果是exp-Loss，那就是牛逼的 Boosting了；如果是log-Loss，那就是Logistic Regression了；还有等等。不同的loss函数，具有不同的拟合特性，这个也得就具体问题具体分析的。但这里，我们先不究loss函数的问题，我们把目光转向“规则项Ω(w)”。

规则化函数Ω(w)也有很多种选择，一般是模型复杂度的单调递增函数，模型越复杂，规则化值就越大。比如，规则化项可以是模型参数向量的范数。然而，不同的选择对参数w的约束不同，取得的效果也不同，但我们在论文中常见的都聚集在：零范数、一范数、二范数、迹范数、Frobenius范数和核范数等等。

四、范数为什么可以防止过拟合
**1，L0，L1范数：**L0、L1主要是用来特征选择，能够将含有信息量小的特征权重优化为0，从而降低特征的维度，从而简化模型。
L0与L1的区别：既然L0可以实现稀疏，为什么不用L0，而要用L1呢？个人理解一是因为L0范数很难优化求解（NP难问题），二是L1范数是L0范数的最优凸近似，而且它比L0范数要容易优化求解。所以大家才把目光和万千宠爱转于L1范数。
稀疏矩阵作用： 大神总结了两点：特征选择以及参数解释

2，L2范数：此正则化偏向于将特征的权重都调整的比较小，分布相对比较均匀，而不是将特征权重调整为0，这样也可以简化模型。（们知道在高次方程中，特别是高次项的系数，是造成曲线陡增（减）的主要因子，我们如果能够将系数调整的比较均匀，那么就能够避免这种过拟合现象的发生。）
大神在这里用很大的篇幅解释一个数学知识，主要说明：L2范数不但可以防止过拟合，还可以让我们的优化求解变得稳定和快速。

五、L1，L2的区别：
其实前面已经提到了区别：L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。Lasso在特征选择时候非常有用，而Ridge就只是一种规则化而已。

这里主要是形式化的说明：对于L1和L2规则化的代价函数来说，我们可以写成以下形式：

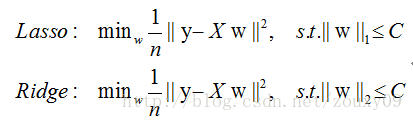
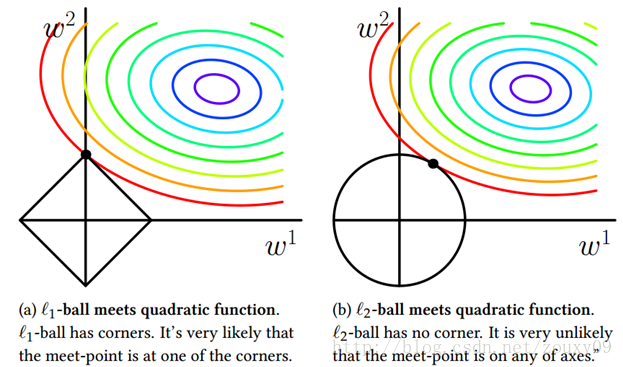
也就是说，我们将模型空间限制在w的一个L1-ball 中。为了便于可视化，我们考虑两维的情况，在(w1, w2)平面上可以画出目标函数的等高线，而约束条件则成为平面上半径为C的一个 norm ball 。等高线与 norm ball 首次相交的地方就是最优解：

可以看到，L1-ball 与L2-ball 的不同就在于L1在和每个坐标轴相交的地方都有“角”出现，而目标函数的测地线除非位置摆得非常好，大部分时候都会在角的地方相交。注意到在角的位置就会产生稀疏性，例如图中的相交点就有w1=0，而更高维的时候（想象一下三维的L1-ball 是什么样的？）除了角点以外，还有很多边的轮廓也是既有很大的概率成为第一次相交的地方，又会产生稀疏性。

相比之下，L2-ball 就没有这样的性质，因为没有角，所以第一次相交的地方出现在具有稀疏性的位置的概率就变得非常小了。这就从直观上来解释了为什么L1-regularization 能产生稀疏性，而L2-regularization 不行的原因了。