使用遗传算法整定PID参数

工具：MATLAB自带的遗传算法工具箱
要求：整定PID调节器调节传递函数

$$\frac{716.23s+13073.64}{s^2+16.88s+45.85}$$

遗传算法工具箱的使用

1.最简单的调用方式

>> [x fval] = ga(@(x) x*x,1)
Optimization terminated: average change in the fitness value less than options.FunctionTolerance.

x =
   -0.0141
fval =
   1.9863e-04

其中ga的第一个参数为适应度函数句柄。

2.当函数较长时，为了方便可以创建一个M函数：

function [ J ] = fitness( x )
% do something
J=x*x;
end

然后这样子写：

>> [x fval] = ga(@fitness,1)

为了自定义算法运行时的参数，可以设置options。
比如想要观察再巡优的过程中各种参数时如何变化的，可以设置PlotFcn;使用help ga命令可以发现官方给的一个参数的设置方式:

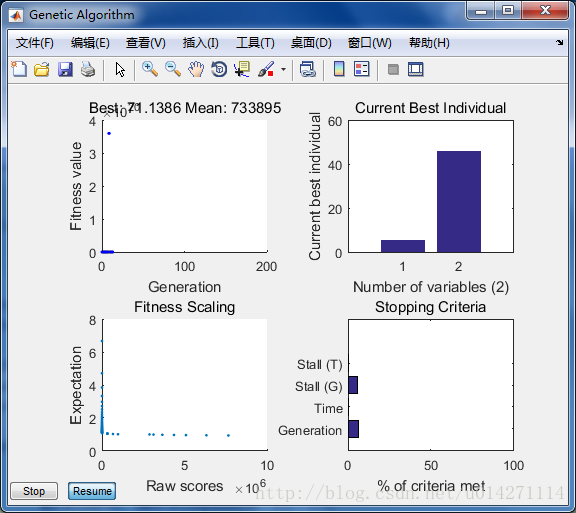
options = optimoptions('ga','PlotFcn',{@gaplotbestf,@gaplotbestindiv,@gaplotexpectation,@gaplotstopping});

最后运行时显示的图像大概是这样的：

详细请参照：最全matlab遗传算法工具箱 教程

获取阶跃响应性能指标

为了方便，这里只采用了PI调节器。
如何获取一个信号的相应的相关性能指标：来源MATLAB中文站

function [ y,tr,ts,pos ] = Performance( PI )
%Performance 求解时域响应的性能指标
%   PI:[KP,KI]
%   tr:上升时间
%   ts:调节时间
%   pos:超调量

PI=tf(PI,[1,0]);

% 此处修改为自己需要调节的传递函数
num=[716.23,13073.64];
den=[1,16.88,45.85];

G=tf(num,den);  %生成传递函数
F=feedback(PI*G,1); %创建单位反馈系统

% t=0:0.02:10;    %20ms
% stepplot(F);
% c=step(F,t);    %动态响应的幅值付给变量c
% plot(t,c)  %绘图，横坐标t,纵坐标c
% grid
[y,t]=step(F,20); %求单位阶跃响应
maxy=max(y);     %求响应的最大值
ys=y(length(y));    %求响应的终值
pos=(maxy-ys)/ys;   %求取超调量
% n=1;
% while y(n)<0.5*ys
%     n=n+1;end
% td=t(n);    %求取延迟时间
n=1;
while y(n)<ys
    n=n+1;
end
tr=t(n);   %求上升时间
n=1;
while y(n)<maxy
    n=n+1;
end
tp=t(n);  %求取峰值时间
L=length(t);
% 倒着寻找
while(y(L)>0.98*ys)&(y(L)<1.02*ys)
    L=L-1;
end
ts=t(L); %求调节时间

end

适应度函数的选择

合理的选择适应度函数才能整定出自己想要的参数：

function [ J ] = MyFitness( PID )
%   MyFitness 此处显示有关此函数的摘要
%   PID:使用遗传算法时，多个参数是按矩阵输入的

%指标的加权系数;调节w1和w3的相对大小，可以表示出对调节时间和超调量的重视程度
w1=1;
w2=0.01;
w3=25;
w4=100000;

%阶跃量
step_num=1;

%调节的时候放大10000倍
PID=PID/10000;

[y,tr,ts,pos]=Performance(PID);
L=length(y);
J1=0;
for index=1:L
    e=step_num-y(index);
    %适应度函数,要求超调量小于0.002
    if pos<0.002
        J1=J1+w1*abs(e);
    else
        J1=J1+w1*abs(e)+w4*pos;
    end
end
J=J1+w3*ts;

end

由于该案例中实际算出来的KP和KI的值比较小，所以，直接使用遗传算法在寻优的时候提供的参数很难得到较为精确的解（比如第一个求X^2的最小值时的情况），但是，整定PI参数是会对系统的输出产生很大的影响，所以，在上面的适应度函数中，将算法工具箱提供的参数都除以10000，相当于最后求出来的参数放大了10000倍，这时候在实际的使用中要记得除以10000。

适应度函数可有有多种选择，以下是在教材上找到的：
1. 误差平方积分：

$$\int_0^ne^2(t)dt$$ 。这个性能指标的特点主要是注重考虑大的误差，而较少的考虑小的误差，因为大的误差平方后更大，在积分中占主导地位，因而这种指标找到最优系统通常是大的起始误差迅速减小，反应较快，但超调量和振幅较大，并且选择性较差，即参数的最优值与非最优值对系统性能指标的影响不明显。

1. 时间乘误差平方积分： $$\int_0^n t \bullet e^2(t)dt$$ 对起始误差考虑较少，而着重考虑过度过程后期出现的误差。
2. 绝对误差积分： $$\int_0^n |e(t)|dt$$ 不论大的或者小的误差，不论早期或者晚期出现的误差均同等对待。
3. 时间乘绝对误差积分： $$\int_0^n t \bullet |e(t)| dt$$

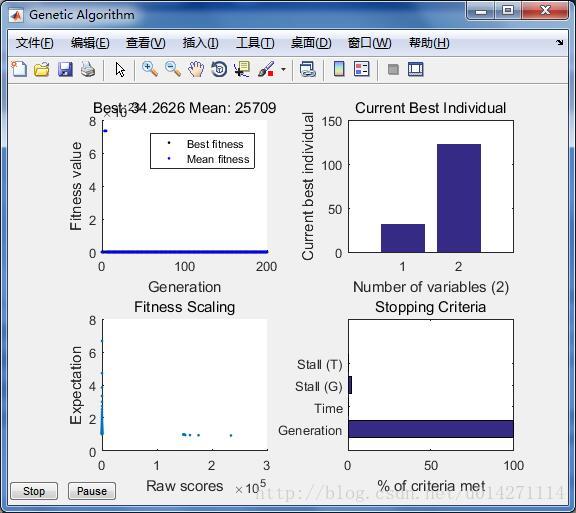
运行结果

>>options = optimoptions('ga','PlotFcn',{@gaplotbestf,@gaplotbestindiv,@gaplotexpectation,@gaplotstopping});
>>ga(@MyFitness,2,options);
Optimization terminated: maximum number of generations exceeded.

ans =

   32.1970  123.0853

每次执行的结果应该会不一样。因为系数放大了10000倍，所以实际的[KP,KI]=[0.00321970,0.01230853]

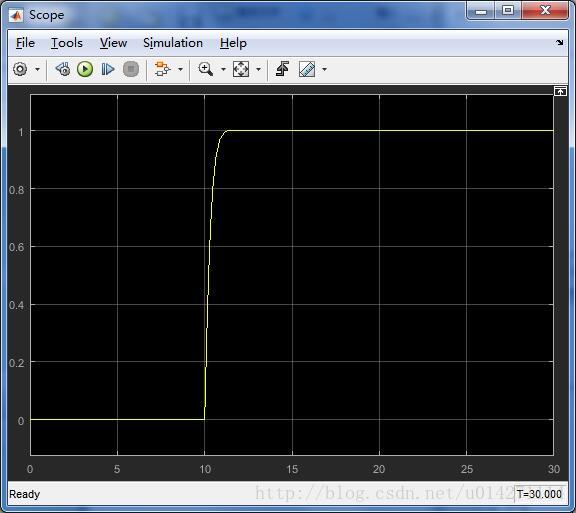
验证：搭建一个Simulink程序进行验证最后的系统的调节过程：

创建自己的输出图形函数

有时候可能options参数里的PlotFcn中的所有绘制数据图像的函数里并没有我们想要的，所以我们可以自己创建相应的绘图函数。

自己写了一个画出当前种群中的每个个体的取值（比较适合优化参数为2的情况，正好一个作为X轴，一个作为Y轴）：

function [ state ] = gaplotindividual( options, state, flag )
%gaplotindividual 绘制当前种群中每个个体的值
%   只适合优化参数为2的情况，其他的情况可以更改绘图函数来实现

% persistent的值在对同一个函数的所有调用中一致
persistent all_data_x;
persistent all_data_y;
persistent all_data_z;

score=state.Score;
population=state.Population;
x=population(:,1);
y=population(:,2);
z=score;
% 记录下所有的历史值
all_data_x=[all_data_x;x];
all_data_y=[all_data_y;y];
all_data_z=[all_data_z;log10(z)];

switch flag
    % 初始化时
    case 'init'
        xlabel KP
        ylabel KI
        title('Individual')
        h=plot(x,y,'*');
        set(h,'Tag','gaplotindividual')
        set(gca,'xlim',[min(x),max(x)],'ylim',[min(y),max(y)])
        title('Current Individual','interp','none')
        xlabel('KP','interp','none');
        ylabel('KI','interp','none');
    % 迭代时
    case 'iter'
        h = findobj(get(gca,'Children'),'Tag','gaplotindividual');
        set(gca,'xlim',[min(all_data_x),max(all_data_x)],'ylim',[min(all_data_y),max(all_data_y)])
        set(h,'Xdata',x,'Ydata',y);

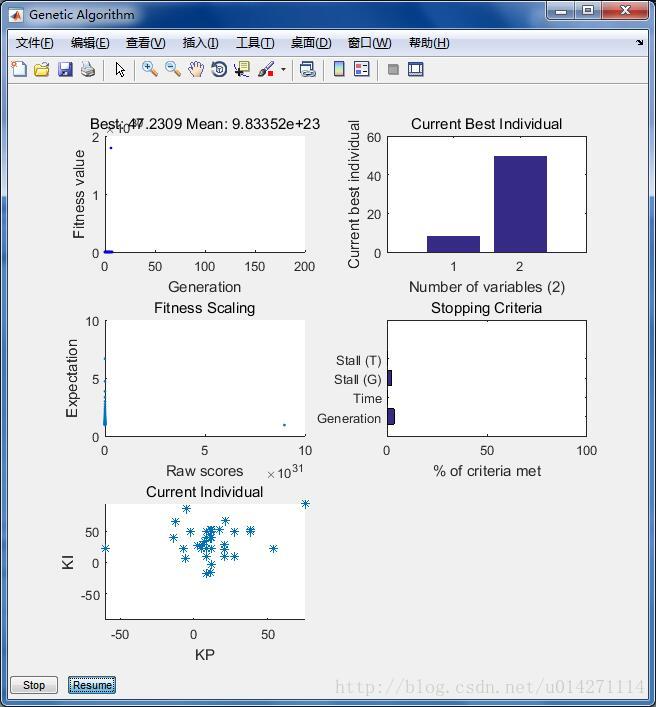
end

运行效果：

入门的最简单的方式，就是看官方的函数是怎么写的，以gaplotbestindiv函数为例，运行edit gaplotbestindiv就打开相应的函数了，然后自己就可以慢慢研究了。