几种常见的数据分布

学习机器学习算法过程中，少不了概率分布的概念，说起概率分布我的脑中除了正太分布那条线就再也没有其他印象了，这个缺陷使我在推导公式过程中遇到很多坑，也在理解数据特征中错过很多。模型的基线取决于数据的好坏，数据的好坏取决与你对数据的理解。所以为了更加懂数据，就先理解一下数据有哪些分布，每次看到一些算法介绍的时候，总是说服从这个分布那个分布，今天索性就把常用的几个总是停留在印象中的分布做个笔记。

均匀分布

这个分布很简单，但是当用到的时候会让你痛苦一会，大家都了解神经网络初始化权重，一般都是随机初始化，但是为了信息更好的在没一层流动，每一层输出的方差应该尽量相等，因此大牛就开始创作了Xavier初始化方法，这个方法得出的结论是，Xavier初始化的实现就是下面的均匀分布，

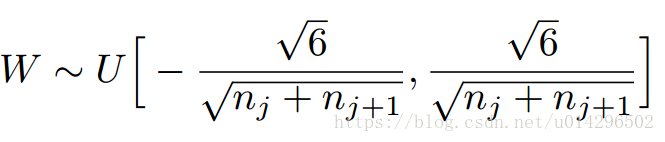
所以在学习各种算法中，你不知道什么时候会有彩蛋，学习权重初始化方法也得先了解均匀分布先。
这个分布理解起来还是很轻松的，就以上面的区间为例，随机取区间内的值X,每个值出现的概率相等。
均匀分布概率密度函数：

$$f(x)=\frac{1}{b-a},a<x<b;否则f(x)=0$$
均值与方差： $$u=\frac{a+b}{2};var=\frac{（b-a）^2}{12}$$

伯努利分布

名字听起来很陌生，其实离我们生活很近，抛硬币都是老掉牙的例子了，正面或者反面。逻辑回归二分类的结果就服从伯努利分布，因为逻辑回归二分类就给出两个结果正例负例。既然结果只有0-1两种，那么很显然它的概率分布就是离散型。
随机变量X服从参数为p的伯努利分布，则X的概率函数：

$$f(x|p)=p^x(1-p)^{1-x} x=0或1$$
均值与方差： $$u=p;var=p*(1-p)$$

二项分布

如果做n次伯努利试验，每次结果只有0，1两种结果，如果n=1的话显然是伯努利分布

举例还以逻辑回归结果举例吧，如果只有一个模型那么结果就服从伯努利分布，如果对样本进行有放回抽样，训练多个逻辑回归模型，则这些模型的输出结果就服从二项分布，举这个例子而不是投硬币是希望能够引起你对bagging的思考。
均值与方差：

$$u=np;var=np*(1-p)$$

泊松分布

假设我们一个产品，统计用户性别比例男性占60%，假设有100个注册新用户，这100个注册用户，有1个为男的概率是多少？有两个为2男的概率是多少？有3个为男的概率是多少？依次下去，显然泊松分布也是离散型分布。

$$P(x)=e^{-\lambda}(\lambda^x/x!)$$
x是100个注册用户性别为男的个数， $\lambda$是先验概率60%
$$P(x;p=0.6)=e^{-0.6}(0.6^x/x!)$$ 有的书里面把 $P(x;p=0.6)$写为 $P(x|p=0.6)$ 看着还挺不舒服的，不知道以为是条件概率。条件概率的话，因为都为变量而不存在常量。
均值与方差： $$u=\lambda;var=\lambda$$

指数分布

同样以app用户注册为例，一个小时注册100个，那么在单位时间为一个小时的前提下，一个男的都没有的概率是多少？把x=0带入泊松分布公式，$P(x=0)=e^{-\lambda}$，则有男性的概率为$P(x!=0)=1-e^{-\lambda}$，则一般形式$P(x)=1-e^{-\lambda t}$,指数分布的应用，如果让你求两个小时内有男人注册的概率你应该会求，对比泊松分布只关注有几个男人注册，而指数分布则只关注是否有男性用户注册。
均值与方差：

$$u=\frac{1}{\lambda};var=\frac{1}{\lambda ^2}$$

https://blog.csdn.net/saltriver/article/details/53982885
https://baike.baidu.com/item/%E4%BC%AF%E5%8A%AA%E5%88%A9%E5%88%86%E5%B8%83/7167021
http://www.cnblogs.com/mikewolf2002/p/7667944.html
https://baike.baidu.com/item/%E6%8C%87%E6%95%B0%E5%88%86%E5%B8%83/776702?fr=aladdin
https://www.jianshu.com/p/d1b7ca81d1af
https://blog.csdn.net/lv_tianxiaomiao/article/details/69389761
https://blog.csdn.net/u013146882/article/details/72998420
https://blog.csdn.net/shuzfan/article/details/51338178