在本篇,你将会看到:
- 量子计算所需要的数学知识
- 量子计算原理
- 尽可能白话讲述
- 量子计算模拟工具,开源免费。(以现在的计算机硬件没办法适用量子计算,但是通过模拟器,可以学习量子计算原理)
阅读本篇之前,所需要的前置条件:
理工科大学生?没问题。只要你已经学完了大学基础课。不推荐高数线代概率没学完的童鞋就来看这个。这个会把你现有的传统计算方式都推翻,会影响考试的~ 但是建议收藏以后慢慢看
理工科大学毕业?没问题,如果你对矩阵的掌握足够自信,不妨来看看。
电气,电子,电学相关学生or工作党? 那可太好了。 学过数字电路,电路等,懂得门控结构什么的。 千万别错过,也许在这场传统二进制计算机革命中,你能在找到工作的同时,推进国家的量子计算研究。记住!只要用电的玩意,就归咱们电气类自动化管!
引言:
不要让那些看似高大上的东西击穿你的意志,或是动摇你的初心。
第一步,忘掉你之前学的计算方法,计算公式,把洛必达,柯西,拉格朗日,微积分啥的都丢一边。保留高斯,欧拉。 只要你知道“矩阵”就够了,稍微带一点概率,概率不懂也没事。 但是“矩阵”是必要条件。
数学基础:
引入狄拉克符号(Dirac notation),即:bra-ket符号
Bras & Kets
- 在矩阵代数中,我们有行和列向量,在狄拉克符号中,我们把这些向量分别写成〈Bras|和|Kets〉。
- 当bras、kets或矩阵彼此相邻时,意味着矩阵乘法。
- Ket ∣a〉:表示向量(通常在复数向量空间中)。
- Bra 〈a∣:是向量的共轭转置(Hermitian 共轭),它是一个“行向量”。

bra和ket写法和意义
在量子计算中,对于行向量和列向量的写法如上图所示。这种写法在量子计算中会更加简洁。 就好比欧米伽符号压缩了多项式求和的写法。
先不考虑Bra,最开始的计算都是ket的计算。(先把罩罩丢掉!)
内积
与大家在大学《线性代数》中学到的内积计算方法一样。点乘。

这个结果是一个复数。
如果|a〉和|b〉是正交的,那么:〈a∣b〉=0,与线性代数中矩阵的知识一样。
当∣a〉是一个归一化向量时,则〈a∣a〉=1。
归一化:一个向量 ∣a〉 是归一化的,意味着它的范数(长度)为 1。范数由向量与自身的内积确定
我们可以把另一个向量描述为向量的组合。如果我们能用一个方便的基来表示一个向量,某些乘法就变得简单了。
比如:

四则混合运算,开括号。
外积:
同样,根据矩阵乘法的规则,我们可以使用ket和bra计算外积:
注意外积的写法,以及外积必须包含bra和ket,不存在两个bra或者两个ket做外积

外积示例
也可以去表示别的矩阵。如:

克罗内科乘积(Kronecker Product)
A⊗B

克罗内克积计算方法
在量子计算中:当两个kets写在一起时,通常表示克罗内克乘积,即|a〉|b〉 = |a〉⊗|b〉。

在量子计算中,我们通过向量来描述计算机的状态,使用Kronecker积可以非常快速地创建包含许多元素的大型矩阵,元素的这种指数增长正是模拟量子计算机的困难所在。
量子计算中的向量和矩阵
仅适用于我们在量子计算中遇到的场景,而不适用于一般的数学。
- 如果两个向量的内积为零,则这两个向量是正交的。
- 如果一个向量的大小为1,那么这个向量就是归一化的。
- 标准正交向量是正交的,也是归一化的。
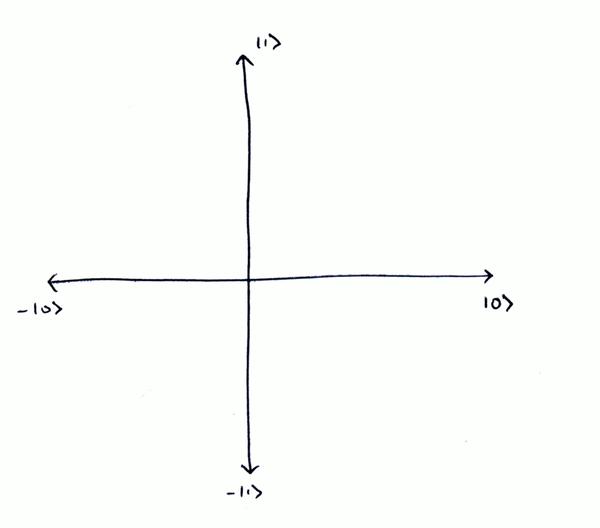
在量子计算中,我们使用正交基向量|0〉和|1〉来表示量子位的开关状态:

量子计算中另一个最常见的二维向量基是由矢量|+〉和|-〉:构成的:

小结一下上面的内容。
如果下面这个图中的内容搞不明白,不建议向下继续,建议搞懂再继续向下看。因为这些都是基础中的基础。

总结
共轭转置
共轭转置,也称为埃尔米特转置,意味着对矩阵和每个元素的复共轭进行转置。在量子计算中,我们用一个十字符号表示共轭转置。
以主对角线为轴,进行翻转,虚部正负号对调,实数元素保留原符号,单单改变位置。
如果理解成普通的转置操作(行列对调),也可以,加上对虚部乘以负一,也是可以的,看个人习惯。

共轭转置
酉矩阵(幺正矩阵,厄米共轭矩阵):
定理:如果一个矩阵的共轭转置是它的逆
- 任何由两个酉矩阵的乘积构成的矩阵也是酉矩阵

Ⅰ通常表示为单位矩阵,ⅠⅠ表示单位矩阵的张量乘积(克罗内科乘积),在量子计算中,用于描述多个量子比特的状态。
厄米尔特矩阵
定理:一个矩阵与其共轭转置相等,则这个矩阵为厄米尔特矩阵。
计算机基础:
- 理工科大学生应该都学习过大学计算机基础,二进制与8421码这种知识没必要在重复一遍了吧
- 时间复杂度,这种东西应该也不用讲
因此我们进行下一部分,量子计算。
量子计算
本篇开始会出现很多抽象切复杂的概念,需要理解,建议对于不懂的词汇一定要及时查询,有的时候发现查询到的解释也包含不懂的词汇,那就再查,递归一样的查。抽丝剥茧去学习,是掌握知识最有效的方法。
量子寄存器(量子位的集合)
量子计算中,一个量子寄存器(也就是多个量子比特的集合)的状态,可以用一个向量 ∣ψ〉来描述,这个向量位于一个叫希尔伯特空间的数学空间里。这个向量 ∣ψ〉 包含了关于这个量子系统的所有信息。
- 什么是量子寄存器?
量子寄存器就像是一个容器,里面放了多个量子比特。每个量子比特可以处于“0”和“1”的叠加态,当这些比特组合起来,它们能表示更多复杂的状态。 - 什么是状态向量 ∣ψ〉?
状态向量 ∣ψ〉 就像是一个“数学坐标”,用来描述量子系统的状态。它把系统的所有可能性都浓缩成一个向量。 - 什么是希尔伯特空间?
希尔伯特空间可以看作是一个多维的空间,每个维度对应系统的某种状态。在经典世界中,我们只关注一条路(比如一个开关是“开”还是“关”),但在量子世界里,系统可以同时处于多种状态的“组合”。
你可以把量子寄存器想象成列表。列表中的每一个元素代表一个量子比特。 但是这个列表你只知道有多少元素。每个位置的元素是0还是1你不知道。 最终在“坍缩”的时候,这个列表才会告诉你输出的结果是0还是1。 因为你看不见列表中每个元素的值,只能去猜测是0还是1,因此每个元素处于0与1的叠加态。
状态向量是希尔伯特空间中的元素。 希尔伯特空间作为多维空间,包含了所有状态可能性,而状态向量是一种状态。
是不是已经开始蒙圈了? 我替你们发出来下面这个表情包。

之前说好的白话解释,就肯定会有白话解释。
但是究一下量子系统的复杂性, 从概率角度也有解释,从向量角度也有解释。 无论哪种解释都是理解角度的一种。与其说是其玄乎,只是举个简单的例子很容易理解,但是想完全理解又不是例子中的那么回事。
我觉得我都快变成叠加态了。。。。。。
这样,咱们举个通俗易懂的例子,但是答应我一件事,别觉得这一个例子理解了,就理解了量子系统,然后乱跟人吹牛学透了量子系统,最后变成我误人子弟。。。(以上为免责声明)
假设我们想描述一个人的“情绪状态”。
希尔伯特空间类比:情绪的所有可能状态
希尔伯特空间就像是一个包含所有可能情绪状态的情绪空间。我们可以假设一个人有多种情绪,如快乐、悲伤、愤怒、平静等等。
- 这些情绪的组合或变化构成了一个情绪空间,就像希尔伯特空间包含了所有可能的量子态。这个空间的维度可以是有限的,也可以是无限的(如果考虑更多复杂的情绪变化)。
状态向量类比:具体的情绪状态
状态向量就像是某个人的具体情绪状态。假设某人现在的情绪是“快乐”的,同时也可能带有一点“平静”,但是不那么愤怒或者悲伤。这个“混合”的情绪状态就是一个状态向量,它是情绪空间中的一个具体向量。
- 如果用数学来表达,假设“快乐”是情绪空间中的一个基向量,记作 ∣happy〉,而“平静”是另一个基向量,记作 ∣calm〉,那么某个人的情绪状态可以表示为:
∣mood〉=0.7∣happy〉+0.3∣calm〉
- 这个状态向量描述了他/她有70%的概率是“快乐”状态,30%的概率是“平静”状态。
量子位
也有称其为“量子比特”的。是量子寄存器中的元素。
一般认为,能够保存信息的最简单的系统是比特。在量子力学中,可以保存信息的最简单的系统是量子位(量子比特)
量子位可以被描述为希尔伯特空间中的一个矢量,不止是量子位的集合(量子寄存器)可以是矢量,量子位也是。
我们称这些维度为|0〉和|1〉.这种矢量行为使得我们的量子位占据了|0〉和|1〉所占据的空间,我们称之为属性叠加。
看下面的图:

我们的量子位q,占据了0和1的ket空间,但是并没有指定是哪个。因此q正处于叠加态~
量子测量的过程
- 在量子力学中,Hermitian算符(记作A)是一个数学操作符,它与量子系统的某些性质相关。例如,它可能表示我们想要测量的某个物理量(如能量、位置等)。Hermitian 是一种特殊的算符,它的特点是它的特征值是实数,这在量子力学中非常重要,因为我们只能测量到实数值。
- 坍缩:量子系统的状态是以叠加态存在的,也就是说,它可以同时处于多个状态中。当我们进行测量时,量子系统的状态会“坍缩”到其中一个确定的状态。这个坍缩是随机的,但有一定的概率。这就像你在做一次选择,系统可能选择某个状态,但你无法完全预测它会选择哪个。
- 特征向量和概率:每个Hermitian算符(A)都有一组叫做特征向量的基础状态。测量时,系统会坍缩到其中一个特征向量。每个特征向量都有一个与之相关的幅度(amplitude),记作a。这个幅度是复数,可以包含大小和相位的信息。|a|² 是幅度a的模方,表示该特征向量发生的概率。换句话说,如果某个特征向量对应的幅度a很大,那么测量时系统坍缩到这个特征向量的概率就很大。
(好家伙, 又是数学家欧拉是吧。)
那么,再举个例子!
假设你有一个量子系统,想测量它的“能量”。你应用一个Hermitian算符A来进行这个测量。A对应的特征向量表示可能的“能量状态”,每个特征向量对应一个能量值。
当你测量系统时,它不会给出一个确定的能量值,而是会“坍缩”到一个特征向量,也就是系统选择一个能量值。选择某个能量值的概率和该能量的幅度(amplitude)有关,幅度的平方(|a|²)表示该能量状态的概率。
例如,如果某个特征向量的幅度a是0.8,那么该能量状态的概率是0.64(即|0.8|²)。这意味着系统有64%的概率选择这个能量值。
回到刚刚那个图上。现在我们应用刚刚理解到的知识,去分析量子位∣q〉

1.量子比特的叠加态
量子比特的状态通常是一个叠加态,比如:
∣q〉=a∣0〉+b∣1〉
这里,a 和 b 是复数系数,它们的模(大小)决定了量子比特处于状态 |0〉 或 |1〉 的概率。
- |0〉 和 |1〉 是量子比特的基状态,可以理解为量子比特的两个“可能”状态。
- a 和 b 是这些状态的“概率幅度”,它们的模方 |a|² 和 |b|² 给出量子比特测量时坍缩到相应状态的概率。
2.坍缩与测量
量子测量时,量子比特的状态会坍缩到测量的结果。例如:
- 如果我们测量这个量子比特,它的状态会坍缩成 |0〉,这种情况发生的概率是 |a|²。
- 如果它坍缩成 |1〉,发生的概率是 |b|²。
这种测量过程是概率性的的,意味着我们无法预知每次测量的结果,只能知道它们的概率。
3.计算基
在量子计算中,常常使用计算基(computational basis)来表示量子比特的状态。计算基是指用 |0〉 和 |1〉 这两个基向量来描述量子比特的状态。每次测量时,量子比特会坍缩成这两个状态之一,这就是测量计算基。
4. 归一化
量子比特的状态向量必须是归一化的,这意味着:
|a|² + |b|² = 1
这条规则是必需的,因为测量的总概率必须为1,也就是说,无论量子比特处于哪种叠加态,最终它必定会坍缩成 |0〉 或 |1〉 中的一个状态,概率之和为1。
5.坍缩导致信息丧失
- 在测量之前,量子比特可以处于叠加态,比如同时具有 |0〉 和 |1〉 的特性,带有不同的概率幅度。
- 但一旦测量发生,量子比特会坍缩,它的状态就会变成 |0〉 或 |1〉 之一,我们丧失了关于量子比特叠加态中其他部分的信息。测量后,你只能得到一个**“是”或“否”**的结果,不能再知道量子比特叠加态中的所有信息。
相位和全局相位
在量子比特的状态中,幅度通常是复数,因此它们有“相位”(即复数的角度部分)。例如,幅度 a 和 b 都可以是复数形式,像这样:
�=|�|���� , �=|�|����
其中 θ_a 和 θ_b 是幅度的相位。
- 全局相位指的是同时施加在所有量子比特上的相位,它是一个整体的旋转,比如把 a 和 b 都乘以一个相同的因子 ��� : �〉=���(�|0〉+�|1〉) 这个全局相位并不会影响量子比特的测量概率,因为我们关心的是幅度的模(即 |a|² 和 |b|²),而相位变化不会改变模的大小。因此,它不会影响我们测量结果的概率。
相位对测量的影响
没啥影响,上面的全可以当做了解一下知识即可。
测量时,我们只关心量子比特状态的幅度的模方,即 |a|² 和 |b|²。这些决定了量子比特坍缩到 |0〉 或 |1〉 的概率。由于全局相位不会影响这些模方,因此它对量子比特的测量没有影响。
布洛赫球
为了方便理解希尔伯特空间中的量子位,我们可以将量子位表示为布洛赫球体上的任意点。
刚刚我们已经缩小了量子位的可能状态;它们的幅度平方必须等于1,我们只关心两个幅度(a和b)之间的相位差。因此,我们可以将任何量子位的状态写成以下形式:

对应球坐标系的θ和ψ。
如下动画所示
布洛赫球表示的量子位
布洛赫球对于可视化单量子位状态非常有用,它将帮助我们理解单量子位操作的效果。
单量子位操作
这一部分是量子计算的各种门计算。 如果看文章的你学过门控电路。 那么对于门结构会有一定了解。如果你是深度学习的爱好者,那么sigmoid激活函数也是一种类似门结构。门结构通常用来过滤,也存在控制功能,比如电路中常见的压控流源等门电路。
X、Y和Z门
X门:
单量子比特量子门可以用一个作用于2D量子比特向量的2×2矩阵来表示。X门就是这样一种门:

X门计算
X门切换了量子位中|1〉和|0〉的振幅,因此它通常被称为“比特翻转”。它也类似于经典的“非”门。
X-gate对叠加态|+〉没有影响,并给|-〉引入了一个负相位,这是因为这些态都是x的本征向量。
实际上X门,在布洛赫球体上,直观的表现是,将布洛赫球体按照X轴旋转180度,就是π。原来的量子位得到新的值。

布洛赫球体上X门,Y门,Z门
同样,Y门是以Y轴旋转180度,原量子位得到新的值,Z门变换是将布洛赫球体(球坐标系)以Z轴旋转180度得到新的坐标系,变换原量子位。
H门(哈达玛门)
参考哈达玛矩阵(离散傅里叶)。

H门
H门的主要作用是将一个量子比特从一个确定的基态(比如 ∣0〉 或 ∣1〉)转化为一个叠加态。这对于量子计算中的许多算法非常重要,特别是在量子并行性和干涉中,以及量子纠缠等。
相移门
同上面H门一样也是一个重要的门
用于对量子比特施加相位变化。相移门的作用是改变量子比特的相位,不改变其幅度。它常用符号 S 或 T 来表示,代表不同的相位变化大小。

作用:
- 相位旋转:相移门主要用于施加量子比特的相位旋转。它不会改变量子比特的幅度(概率振幅),只会改变其相位。通过组合多个相移门,可以实现更复杂的量子操作。
- 量子傅里叶变换:相移门是量子傅里叶变换(Quantum Fourier Transform, QFT)的核心组件之一。QFT是许多量子算法中的一个重要部分,尤其是在量子算法如Shor的因式分解算法中。
- 量子纠缠:在构造量子纠缠态时,配合其他量子门(如Hadamard门和CNOT门),相移门可以用于调节量子态的相位,增强量子态的纠缠性。
量子电路
各位在看量子计算的文章,或者github上项目,都会发现一个Quantum Circuit,量子电路。
量子电路是量子算法的实现框架,可以理解为量子比特(Qubits)的操作序列。
1. 量子电路的基本组成
量子电路是量子算法的实现框架,可以理解为量子比特(Qubits)的操作序列。
- 量子比特:信息的最小单位,可表示为 ∣0〉|0〉∣0〉、∣1〉|1〉∣1〉 或它们的叠加态。
- 量子门:类似于经典逻辑电路中的逻辑门(如与门和非门),量子门对量子比特进行操作。例如:
- HHH 门(Hadamard Gate):创建叠加态。
- XXX 门:类似经典的 NOT 门。
- CNOTCNOTCNOT 门:条件翻转门,用于创建纠缠态。
- 测量:量子态坍缩到经典比特值(0或1)。
2. 量子电路的运行逻辑
量子电路按照时间顺序执行一系列量子门操作。一个典型的量子电路包含以下步骤:
- 初始化量子态:将所有量子比特初始化为 ∣0〉|0〉∣0〉。
- 施加量子门:按照量子电路的设计对量子比特操作。例如,将 HHH 门应用于第一个比特,使其处于叠加态。
- 测量量子态:最后对量子比特进行测量,输出经典信息。
示例,如下是一个简单的量子电路,初始态,经过多个门结构,最后测量值。

量子电路示例
对于深度学习人员来说,可以理解为时间步操作。
量子电路经典示例,
真正的随机数生成器:
对于目前已有的随机数生成,其并不是随机的,而是基于算法以及时间戳,物理机地址,cpu时钟信号等等条件,计算得到的。
而量子计算是真正的随机生成:不依赖任何条件,单纯的量子纠缠态坍缩观测得到的结果,在观测之前,也许就算是上帝也不知道是啥结果。
下面是一个示例,但是这个示例在目前没有办法在现有的市面上能接触到的计算机实现。

随机数生成器
把4个初始态,经过H门,进行变换,然后观测。
在H门之后,每个量子位的状态是|+〉,是一个纠缠态。
纠缠态,值为0和1的振幅(概率)都是50%。真正的随机生成0或1。
落在哪个值区域,在测量之前,没有人能推测,也没有任何条件可以推测。
两个量子比特操作
受控X门(CNOT):
CNOT门(Controlled-NOT门),也叫做受控非门,是量子计算中最重要的基本量子门之一。CNOT门是一个两量子比特门,它有两个输入:一个控制比特和一个目标比特。CNOT门的作用是:
- 如果控制比特是 ∣0〉,则目标比特不变。
- 如果控制比特是 ∣1〉,则目标比特会翻转(从 ∣0〉 翻转到 ∣1〉,反之亦然)。
在传入量子位时,除了目标比特(需要转换的量子比特),还要输入一个控制位。

CNOT
控制位控制着是否执行X门翻转,0代表不执行,1代表执行。当输入10时,代表着对0执行X门操作,将0翻转为1。
更多示例:
1.
假设我们有一个量子比特对 ∣00〉(控制比特为 0,目标比特为 0)作为输入状态:
CNOT(∣00〉)=∣00〉
因为控制比特为 0,CNOT门不改变目标比特的状态,所以结果仍然是 ∣00〉。
2.
对于输入状态 ∣11〉(控制比特为 1,目标比特为 1):
CNOT(∣11〉)=∣10〉
因为控制比特为 1,CNOT门会翻转目标比特的状态,从 ∣1〉|1\rangle∣1〉 变为 ∣0〉,所以输出是 ∣10〉。
纠缠
纠缠是量子计算能力超越经典计算的核心要素之一,因此在量子计算中极其重要
量子纠缠就很有意思了,之前我们使用的是普通态输入进CNOT门,那么当我们把叠加态(∣+〉、∣-〉)输入进CNOT的控制位,会产生什么效果呢?
叠加态放目标位没什么意思,也是使用X门进行翻转。 但是如果把叠加态放在控制位,不是传统的0不执行,1执行。
那么量子就会进入纠缠状态。
过程如下所示:

示例
输出的量子态 |�〉=12(|00〉+|11〉) 是一个 纠缠态(Bell 态)。这是量子纠缠的经典例子,控制比特和目标比特的状态紧密关联:
- 如果测量控制比特为 ∣0〉,目标比特必然是 ∣0〉。
- 如果测量控制比特为 ∣1〉,目标比特必然是 ∣1〉。
上面这两句话,个人认为就是最精彩的部分,本来不可控的变为可控。并且由于0和1出现了纠缠态,纠缠态即可以是1也可以是0(可攻可受),因此携带的信息并不是三进制,是比三进制多好多的数据,只要有办法控制观测结果,可以在同样的资源下,携带更多的信息。
在 |�〉=12(|00〉+|11〉) 中,∣00〉与∣11〉,在这种状态下,我们已经不能把他们写成2阶矩阵了,他们实际上已经是“融合”状态。 测量测量任意一个的状态,都会直接破坏掉另一个的状态。 (修罗场二选一)
休息一下,喘口气。 接下来的内容是一个好用的量子电路模拟器。
之所以说是模拟器,因为用于量子计算的硬件都是定制的,不是我们市场上能买到的CPU啥的就能做计算的。
但是有国外大佬为了方便理解,把量子计算原理做成了模拟器,用于学习。
切记:并不是这玩意后台挂着一个真正的量子计算机。。。。。。
量子电路模拟器
量子电路模拟器,有很多,有免费的有收费的。
如:
- IBM的Qiskit Aer,支持python编程,适用于开发算法,研究验证。
- PennyLane,结合了pytorch,keras,适合深度学习,用于量子机器学习研究。
- 亚马逊的Braket,适合云端开发量子算法
- TensorFlow Quantum,谷歌的量子深度神经网络研究社区。
- Atos Quantum Learning Machine,适用商业量子算法开发
但是以上这些我们都不用,我们使用Quirk来演示。
Quirk是一个量子电路模拟器, Quirk的运行只需要浏览器,不需要安装,提供即时反馈,可以处理多达16个量子位。
要使用Quirk,单击一个门并将其拖动到线路上。要移除门,可以用鼠标中键点击它或将它拖出屏幕。我们将使用Quirk来演示一些电路特性,建议理解了上面所有内容的你一起尝试这些电路。
Quirk-在线量子计算模拟器algassert.com/quirk
Quirk官方代码仓以及教程github.com/Strilanc/Quirk/wiki/How-to-use-Quirk
打开量子计算模拟器,可以看到这样的界面

Quirk
点击“Edit Circuit”,开始玩耍

Quirk界面
接下来我们将使用Quirk,将刚刚学到的CNOT门进行演示。
在Quirk中,所有的功能都以积木方式可以拖动,鼠标悬停可以查看功能说明。
执行下面的操作

黑点代表量子比特控制开,另一个中间加了十字的圆,是刚刚说的X门
量子位开始于|00〉状态,结束于|00〉状态(两个量子位都是关闭的)。
off方块代表观测量子状态,后面的球代表布洛赫球体,方便观看相位旋转角。
在后面的是观看振幅。
现在,我们设定了上面那条线是控制量子位,下面这个是X门。这样组成了一个CNOT门,通过控制位判断X门是否执行对第二条线的量子位翻转。
我们可以点击∣0〉和∣1〉改变输出,来查看效果,如下图:

点击切换量子初始态
当控制位置1时,X门对输入的∣0〉初始态执行翻转,在观测时,振幅(落在值的概率)百分百在∣11〉

将控制量子位置1
剩下的别验证了。 这个模拟器有BUG。 计算结果是错误的。以下是错误展示。 等修复吧。

错误展示
实际上控制位∣1〉不变,将目标位∣1〉进行翻转成为∣0〉,最终的输出结果应该是∣10〉。 本厮试了好几次,都把0和1弄反了,可恶。 这是个bug,等他们修,感觉是X门的计算出现bug。
不过,只要能帮助理解量子计算,就是好的。
我们继续。
创建基本叠加
到目前为止,我们实际上还没有看到任何量子效应。
让我们给一个量子位加一个H门。观察布洛赫显示,我们看到量子位处于预期的|+〉状态。
我们将一个初始态|0〉,经过H门变换成为叠加态|+〉。振幅概率为|0〉和|1〉各为50%

H门将初始态转换成叠加态
布洛赫球的效果,配合下面这个图看。

布洛赫球
按照指向,我们可以看到初始态转换成了叠加态|+〉。
现在,让我们通过在h门之后添加z门来创建|-〉状态。我们看到我们的量子位状态有相同的|0〉和|1〉数量级,但是它的相位改变了。
还记得Z门是将初始态(输入量子位)以Z轴旋转180度吗?

H门+Z门
对照上面的布洛赫球坐标系的图。 可以更直观的理解。
这个地方没有bug,是正确的的(我发四~)
纠缠
接下来将使用模拟器演示量子纠缠
刚刚展示了一个量子纠缠状态(贝尔态,Bell),还记得如何得到的吗?
我们将CNOT的控制位输入的不是|0〉和|1〉,而是输入了一个叠加态到控制量子位。
在量子电路模拟器中,我们先让初始态,经过H门变为叠加态,再将叠加态输入到CNOT的控制位。

量子纠缠展示
可以直观的看到我们的布洛赫球已经放弃了,因为我们的量子比特已经纠缠在一起,我们不再能够独立地描述它们的状态。我们可以查看振幅显示来了解整个系统的状态。

量子纠缠振幅
|00〉和|11〉的振幅相等,为 12 ,也就是val中的0.70711。

量子纠缠
使用“chance”块添加到电路中,并覆盖两条线,如下图所示

chance块
chance帮我们查看测量量子位组合的概率。我们可以看到,我们有50%的机会测量两个关闭和两个打开,但不可能出现测量一个打开和一个关闭(将光标悬停在显示屏上以查看对话框)

也就是说,只能有|00〉和|11〉,才有50%测量。对应公式: |�〉=12(|00〉+|11〉)
量子电路算法
Deutsch-Jozsa算法
Deutsch-Jozsa算法是量子计算中的一个重要算法,它解决了一个特定类型的黑箱(black box)问题,展示了量子计算在某些问题上相较于经典计算的优势。
接下来的内容,对于学过单片机,或者其他电子元器件的童鞋来说,会容易理解一些。
加法电路可以将两个二进制数存入两个寄存器(我们称一组位为一个寄存器),并将它们的和输出到其中一个寄存器:

传统加算电路
在量子计算领域中,下面是Quirk的创造者提供的一个例子(加算量子电路):
Quirk作者给出的这个示例可能会有一些难以理解(如果有计算机硬件开发底子的佬应该会理解),但是耐心一些,后面会有解答(不是立刻解答)。
在量子计算中,我们经常使用一种不同的计算方式,解决我们所谓的“黑箱”问题。黑箱只是一个量子电路,我们不允许查看或拆开它。在这种情况下,问题的实例被编码到我们执行的操作中,而不是输入寄存器中:

Deutsch-Joza黑箱问题(经典量子问题举例)
现在,假设我们有一个经典的Deutsch-Joza黑箱(记做函数� ),它接受n个输入量子位,并输出到一个输出量子位:

Deutsch-Joza黑箱
先了解另一个重要概念,电路可逆
在量子计算中,量子操作必须是可逆的,量子态的演化必须保持信息,量子操作是由 unitary(酉)变换定义的,而酉变换是 可逆的。
由于量子态是向量的形式(通常表示为复杂向量空间中的一个状态),量子操作必须能够“反向”,否则信息将会丢失。
同时,在测量阶段,“坍缩”会造成不可逆的量子信息损失。因此无论在哪个电路的量子操作,都必须保证该电路可逆。
因此,量子算法的设计要求:
许多量子算法,特别是如 Deutsch-Jozsa算法 这样的算法,需要通过量子操作来“编码”和“解码”信息。在 Deutsch-Jozsa算法 中,通过一个量子oracle(黑箱)来进行查询时,我们需要能够有效地执行这些操作并最终恢复准确的结果。如果oracle操作不可逆,可能导致测量时丢失关键信息,导致无法判断函数的性质。
为此,我们必须引入一个oracle,作为控制量子位,同时电路设计成可逆的。
为了使量子电路可逆,我们需要调整黑箱(oracle)的设计,使其具有与输入量子比特相同数量的输出量子比特,也就是说,操作后的结果必须能够通过某种方式恢复到原来的输入状态。
为了使电路可逆,我们需要调整我们的黑盒,使其具有与输出量子位相同数量的输入量子位。在我们的例子中,我们给电路n个输入量子位加上一个额外的输出量子位,电路返回初始状态的原始n个输入量子位,加上新状态的输出量子位。
如下所示:

电路可逆
现在,抛出需要解决的问题:
Deutsch-Jozsa算法 中黑箱(oracle)函数的两种可能输出类型:常函数(constant)和平衡函数(balanced)。
- 一个 常函数 的特点是,无论输入是什么,它的输出始终保持相同。
- 一个 平衡函数 的特点是,它的输出在所有输入上是 均匀分布的。具体来说,对于所有可能的输入,输出 1 的次数与输出 0 的次数是 相等的。如:输入四个数,输出只有0和1两个值,如果是平衡函数,输出必须是两个0两个1
我们的任务是通过查询 oracle,判断该函数到底是哪一种类型,而 Deutsch-Jozsa算法 只需一次查询就能确定这一点。
经典算法中的解决方法:
在经典计算中,我们不能像量子算法那样通过叠加和干涉一次性解决问题。因此,我们需要通过查询黑箱函数 �(�) 的不同输入值,来判断它是常函数还是平衡函数。
要以 100% 确定性证明黑箱是常函数,我们需要检查超过一半的可能输入状态(即 2�−1+1 次查询)。不过,如果我们愿意接受一个小的误差范围,所需的查询次数会少得多。
经典解法在最好的情况下需要 2 次查询,在最坏的情况下需要 2�−1+1 次查询。而 Deutsch-Jozsa算法 只需要一次查询。
使用Deutsch-Joza算法
- 将输出量子位设置为|-〉
- 将H门应用于n个输入量子位
- 运行黑箱
- 将H门应用于n个输入量子位
- 测量n个输入量子位:
- 如果所有的n个量子位都处于|0〉状态,盒子是不变的
- 否则,盒子是平衡的
下面是量子电路图:

Deutsch-Jozsa算法
我们为了验证这个black box是常函数,还是平衡函数。将所有的输入都变成叠加态,即包含0也包含1。
黑箱中的操作,必会改变输出结果的概率幅度
- 如果函数 �(�) 是 常函数,所有输入比特的干涉效应会增强 ∣000〉 的概率幅度,其余态的幅度抵消。因此,测量结果一定是 ∣000〉。
- 如果函数 �(�) 是 平衡函数,干涉效应会导致 ∣000〉 的概率幅度为零,其他态有非零概率。
总结一下过程:
- 第一次 HHH 门:将输入比特初始化为均匀叠加态,辅助比特初始化为相位态。
- 黑箱 � :根据函数�(�)改变辅助比特的相位。
- 第二次 HHH 门:通过干涉效应提取函数的性质。
- 测量输入比特:如果测量结果是 ∣000〉,函数是常函数;否则是平衡函数。

其中:
- “on” 通常表示测量结果为 ∣1〉。
- “off” 通常表示测量结果为 ∣0〉。
各位童鞋可以自行在模拟器里面添加模块,比如在最后一条电路上加上H门,我自己试的是,A黑箱是一个常函数。动手会帮助直观的理解量子电路。
上面的算法是一个量子计算中的示例。
下面是更多的算法(超级抽象),感兴趣的可以挑战一下,搜索关键词研究。
本厮暂时没参悟透(这是重点)。
量子算法更多示例:
格罗弗算法(格罗弗算法)
格罗弗算法,也称为‘量子搜索’和‘振幅放大’,是一种针对非结构化数据库的搜索算法。它对于量子计算机来说是可证明的最佳算法,并且比最好的经典算法快一倍。
洛夫·格罗弗(Lov Grover)在1986年发表了他的算法:A fast quantum mechanical algorithm for database search
量子傅里叶变换
量子傅里叶变换(QFT)是量子计算中的一种算法,它是经典傅里叶变换的量子版。QFT用于将量子态从标准基(如 ∣0〉,∣1〉)转换为频率基。通过 QFT,量子计算机可以以指数级加速的方式执行傅里叶变换,尤其在解决问题如素因数分解、Shor算法中非常关键。QFT的核心是利用量子叠加和干涉效应,减少计算所需的步骤数,从而提供比经典算法更高效的解决方案。
量子相位估计(QPE)
基本思路是通过量子叠加和干涉过程来精确估计相位。它利用了量子叠加态的并行性,显著减少了估计的时间复杂度,通常能在多项式时间内实现高精度估计,相比经典方法具有优势。
肖尔算法
用于整数因式分解。它能够在多项式时间内比经典算法更快地分解大整数,具有重要的加密学意义,尤其能破解像RSA这样的加密系统,这些系统的安全性依赖于大数分解的困难。肖尔算法利用量子并行性,解决了两个关键子问题:计算函数的周期并利用周期来进行因式分解。这展示了量子计算在解决传统计算无法处理的问题中的潜力。
线性方程组的量子算法
对应机器学习的诸多问题。
到这里,量子计算系统的入门中的入门教程,就完毕了。
希望看完文章的你,解决了下面的疑惑:
- 这玩意是不是画大饼?
- 这玩意玄玄乎乎的,什么“遇事不决,量子力学”,这玩意真就那么神?
- 量子计算有科学依据吗?
- 我这水平能入行量子计算领域吗?
当然,本厮在看过那些经典算法后,才发现,直到目前,都只是小儿科一样的东西。 本篇学到的内容,可以比喻成量子计算领域的“加减乘除运算”。
当然了,鼓励大家都挑战一下上面那些经典算法,本厮也会继续搞一下,因为:
- 不试试,你永远不知道自己的极限在哪里。
- 对于一个“好学生”的定义,不应该是只学会一板一眼知识,而是学会解决问题的方法。
- 本篇能带来的知识有限,能找到解决疑惑的文章也是必备的素质之一。
- 人类的智慧挺了不起的。
回到开头的引言作为结尾:
不要让那些看似高大上的东西击穿你的意志,或是动摇你的初心。
【量子计算】量子计算入门,适合本科毕业生入门原理讲解
(完)























 1214
1214

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








