2024年9月4日更新:
- 优化了等高线生成算法,支持百万级三角形
2023年6月16日更新:
- 优化了等高线生成算法,大幅提升效率
- 修复test.py绘制报错的问题(与依赖库更新有关)
一、研究背景
在GIS场景中,有很多面要素类型的数据,如地层面、水位面等,这些面的数据格式基本都是三角网,而基于这些数据生成等高线是用户常用的需求,网上搜索了一番也没有找到可直接用于生成的库,为此自研了基于python语言的三角网生成等高线的算法。
二、等高线的两种情况
使用过等高线的用户应该知道,在一个有限范围的平面图上,等高线是一系列高程相同的点的连线,由于范围有限,这些连线会出现闭合和不闭合两种情况。
三、算法思考
3.1 从几何的角度看等高线
- 从宏观上看:等高线可以看成是具有相同高程间隔的一系列水平面与目标面(如地层面、水位面等)求交得到的交线集合。且不闭合的线的端点在面的边缘。
- 从细节上看:等高线是具有相同间隔的
z平面集与三角网的三角形的三条边的交点的连线的集合。且不闭合的线的端点在三角形的非共有的边(该边不同时属于两个三角形)上。
3.2 基本准则
根据上述的思考,建立如下算法准则
- 如果三角形的某条边与某
z平面相交,则有且仅有另一条边与该z平面相交 - 如果等高线的起点为三角形的非共有的边,则终点必然为另一个三角形的非共有的边
- 如果一个点为闭合等高线上的点,则不论沿哪个方向搜索,都能遍历完所有的点并回到自身原点
- 非闭合等高线的点从端点开始可遍历完线上所有的点,且不会回到自身原点
3.3 实现算法
根据上述准则,建立如下某z平面与三角网求交线的算法
- 先从三角网数据中解析出所有不重复的线段,并记录每条线段所属的三角形索引号
- 计算每条线段与
z平面的交点(插值计算),如果有则保存点坐标并记录该点所属的线段索引号 - 为每个点设置是否被使用的标记
- 先寻找属于非闭合等高线的点:循环遍历交点集,判断点是否被使用,已使用则跳过,未使用则根据点所属的线索引号找到线所属的三角形列表,判断列表大小,如果为
2,则说明该线段为共有边,此时跳过该点;如果所属三角形列表大小为1,则说明为非共有边,可作为非闭合等高线的起点开始搜索。根据准则1,可以寻找当前点所属的线所属的三角形(因为是非共有边,可以确定该三角形)的另外一个交点,如此往复,可以得到一条非闭合等高线线的点集,这些点集都标记为已使用。一条线遍历完后,重复上述流程,直至找不到非共有边上的点。这样我们就得到了所有非闭合的等高线。 - 然后寻找闭合等高线的点:循环遍历交点集,判断点是否被使用,已使用则跳过,未使用则根据
准则1,可以寻找当前点所属的线所属的三角形(因为是共有边,有2个三角形,选任意一个即可)的另外一个交点,如此往复,可以得到一条闭合等高线线的点集,这些点集都标记为已使用。一条线遍历完后,重复上述流程,直至找不到未标记的点。这样我们就得到了所有闭合的等高线。
根据上述流程可以得到某个z对应的线,用户一般只提供z_interval(间隔),并不指定具体是哪些z值需要算,此时还需要计算z值列表,本文的算法是先获取面的z_max和z_min,然后找到大于z_min的z_interval的倍数值,以此为起始累加z_interval,直到大于z_max
四 算法编写
- 构建
Tin类来承载三角网的数据结构以及相关计算方法,三角网的数据源选用市面上常用的stl文件(测试文件百度网盘下载链接:https://pan.baidu.com/s/1T1DRpI3nExAcryXt_izB9g提取码:sxvg) - 由于用到了
stl文件,需安装stl解析库pip install numpy-stl
# pip install numpy-stl
from math import ceil
from stl import mesh
class Tin(object):
"""三角网类:用于封装三角网的数据结构,以及外部三角网数据的读取、三角网生成等高线等功能
"""
def __init__(self) -> None:
self.__tin = None # 三角网格格式数据:由三个点坐标构成的三角形集合,如[[[0, 0, 0], [1, 0, 0], [1, 1, 0]], [[1, 0, 0], [2, 1, 0], [1, 1, 0]]]
self.__box = None # 三角网的包围盒:由左下角点和右上角点组成,如[[0, 0, 0], [1, 1, 1]]
def init_from_data(self, tin:list):
"""直接用三角网数据初始化
:param list tin: 三角网格格式数据
"""
self.__tin = tin
def init_from_stl(self, path:str):
"""从stl文件读取三角网数据
:param str path: stl文件路径
:param bool return: True-读取成功/False-读取失败
"""
try:
data = mesh.Mesh.from_file(path)
self.__tin = data.vectors.tolist()
self.__box = [[data.x.min(),data.y.min(),data.z.min(),],
[data.x.max(),data.y.max(),data.z.max(),]]
return True
except Exception as e:
print(repr(e))
return False
def get_tin(self):
"""获取三角网的数据
:return list self.__tin: 三角网数据
"""
return self.__tin
def get_box(self):
"""获取三角网的包围盒
:return list self.__box: 包围盒
"""
return self.__box
def generate_contour(self, z_interval:float):
"""生成等高线
:param float z_interval: 等高线z间隔
:return list contour: 等高线数据
"""
# step1: 判断三角网是否有存在
if self.__tin == None or len(self.__tin) == 0:
print("Error: 三角网格不存在")
return None
# step2: 从tin中获取线的信息以及坐标的最值
z_min, z_max, lines, lines_belongto_tri = self.__get_lines_from_tin()
# step3: 获取等高线的z值列表
z_set = self.__get_z_value_set_by_interval(z_min, z_max, z_interval)
# step4: 使用每个z平面与三角网格面求交线
contour = []
for z in z_set:
pts, pts_belongto_line = self.__get_inter_pts_between_lines_and_z_plane(lines, z)
uses_pt = [False]*len(pts) # 点是否被使用,默认False
polylines = []
# 先获取非闭合的
while True:
start = -1
for idx, use in enumerate(uses_pt):
if not use and len(lines_belongto_tri[pts_belongto_line[idx]]) == 1:
start = idx
break
if start == -1:
break
polyline = []
self.__get_next_pt(start, uses_pt, pts_belongto_line, lines_belongto_tri, polyline)
polylines.append(polyline)
# 再获取闭合的
while True:
start = -1
for idx, use in enumerate(uses_pt):
if not use:
start = idx
break
if start == -1:
break
polyline = []
self.__get_next_pt(start, uses_pt, pts_belongto_line, lines_belongto_tri, polyline)
polyline.append(polyline[0])
polylines.append(polyline)
# 将索引转成坐标
for idx_line in polylines:
contour_pts = []
for idx_pt in idx_line:
contour_pts.append(pts[idx_pt])
contour.append(contour_pts)
return contour
def __get_lines_from_tin(self):
"""从self.__tin中解析出所有不重复的线段以及点z坐标的最值
:return float z_min: 三角网的最小z值
:return float z_max: 三角网的最大z值
:return list lines: 三角网中的线段(两个点),每一项都是两个点的集合,如[[[],[]],[[],[]],[[],[]]...]
:return list lines_belongto_tri: 每条线所属的三角形索引号,每一项都是一个列表,记录所属三角形索引号的集合
"""
lines = []
lines_belongto_tri = []
z_min = 1e10
z_max = -1e10
# 遍历三角网
line_map = {}
next_line_idx = 0
for idxTri, tri in enumerate(self.__tin):
# if idxTri % 10000 == 0:
# print(idxTri)
line1 = f"{tri[1]}_{tri[0]}"
line1_idx = line_map.get(line1)
if line1_idx == None:
lines.append([tri[0], tri[1]])
lines_belongto_tri.append([idxTri])
line_map[f"{tri[0]}_{tri[1]}"] = next_line_idx
next_line_idx += 1
else:
lines_belongto_tri[line1_idx].append(idxTri)
line2 = f"{tri[2]}_{tri[1]}"
line2_idx = line_map.get(line2)
if line2_idx == None:
lines.append([tri[1], tri[2]])
lines_belongto_tri.append([idxTri])
line_map[f"{tri[1]}_{tri[2]}"] = next_line_idx
next_line_idx += 1
else:
lines_belongto_tri[line2_idx].append(idxTri)
line3 = f"{tri[0]}_{tri[2]}"
line3_idx = line_map.get(line3)
if line3_idx == None:
lines.append([tri[2], tri[0]])
lines_belongto_tri.append([idxTri])
line_map[f"{tri[2]}_{tri[0]}"] = next_line_idx
next_line_idx += 1
else:
lines_belongto_tri[line3_idx].append(idxTri)
# 获取Z的最值
for pt in tri:
if pt[2] < z_min:
z_min = pt[2]
if pt[2] > z_max:
z_max = pt[2]
return z_min, z_max, lines, lines_belongto_tri
def __get_z_value_set_by_interval(self, z_min:float, z_max:float, z_interval:float):
"""根据阈值和步长得到z数组
param: float z_min: z的最小值
param: float z_max: z的最大值
param: float z_interval: z的步长
return: list z_set: z数值列表
"""
z_set = []
z_interval_new = int(z_interval)
# 找到z的起始
z_input = ceil(z_min/z_interval_new) * z_interval_new
while True:
if z_input > z_max:
break
z_set.append(z_input)
z_input += z_interval_new
return z_set
def __get_inter_pts_between_lines_and_z_plane(self, lines:list, z:float):
"""获取线集和z平面的交点
param: list lines: 线段集合
param: float z: 高程值
return: list pts: 交点集合
return: list pts_belongto_line: 每个点所属的线段索引号
"""
pts = []
pts_belongto_line = []
for idx, line in enumerate(lines):
# 判断z是否在线段之内
if line[0][2] <= line[1][2]:
pt = self.__inter_by_z(line[0], line[1], z)
else:
pt = self.__inter_by_z(line[1], line[0], z)
if pt != None:
pts.append(pt)
pts_belongto_line.append(idx)
return pts, pts_belongto_line
def __inter_by_z(self, pt_min:float, pt_max:float, z:float):
"""计算线段与z平面的交点
param: list pt_min: 线段中z较小的点
param: list pt_max: 线段中z较大的点
param: float z: z值
return: list pt: 交点
"""
pt = None
if pt_min[2] != pt_max[2] and z >= pt_min[2] and z <= pt_max[2]:
rate = (z - pt_min[2])/(pt_max[2] - pt_min[2])
x = pt_min[0] + rate*(pt_max[0] - pt_min[0])
y = pt_min[1] + rate*(pt_max[1] - pt_min[1])
pt = [x, y, z]
return pt
def __get_next_pt(self, start:int, uses_pt:list, pts_belongto_line:list, lines_belongto_tri:list, contour:list):
"""获取同一个三角形的其他边的交点
param: int start: 交点的索引号
param: list uses_pt: 交点是否被使用的标记
param: list pts_belongto_line: 交点所属的线段索引号
param: list lines_belongto_tri: 线段所属的三角形索引号
param: list contour: 由点索引号组成的等高线数据
"""
contour.append(start)
uses_pt[start] = True
for cur_tri_idx in lines_belongto_tri[pts_belongto_line[start]]:
for idx_pt, use_pt in enumerate(uses_pt):
if use_pt:
continue
for idx_tri in lines_belongto_tri[pts_belongto_line[idx_pt]]:
if cur_tri_idx == idx_tri:
self.__get_next_pt(idx_pt, uses_pt, pts_belongto_line, lines_belongto_tri, contour)
return
五 算法测试
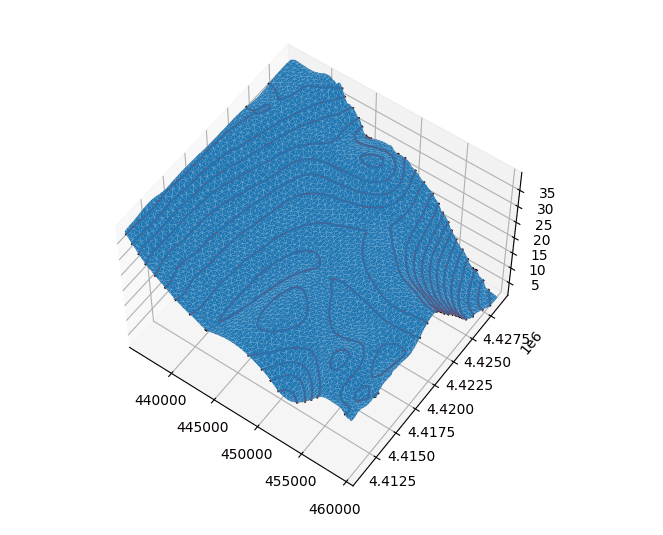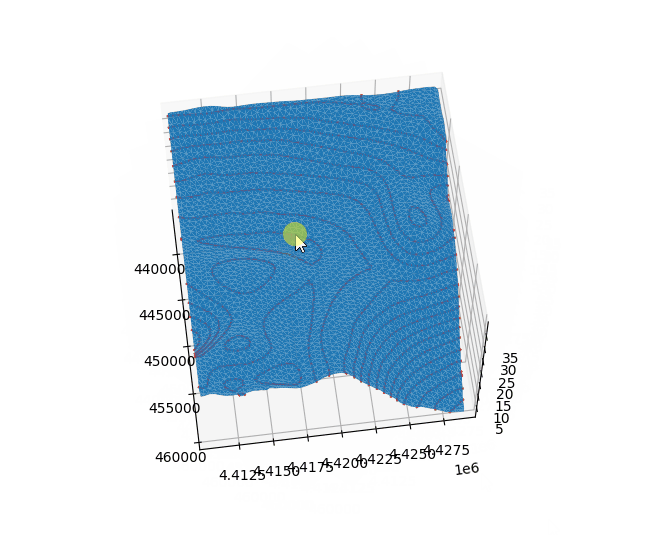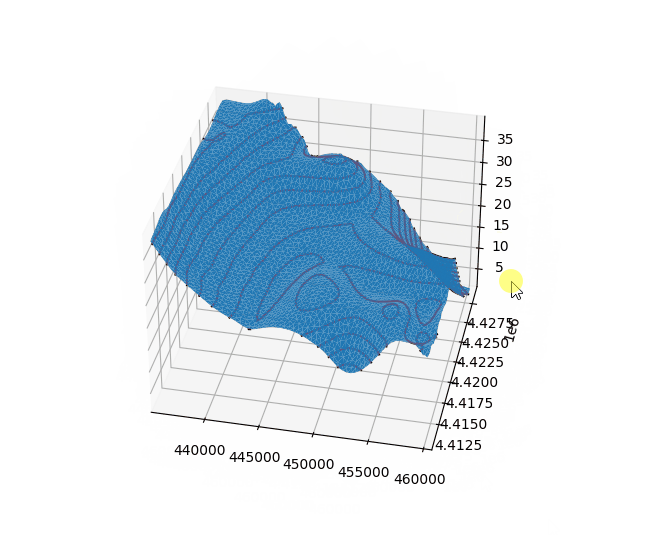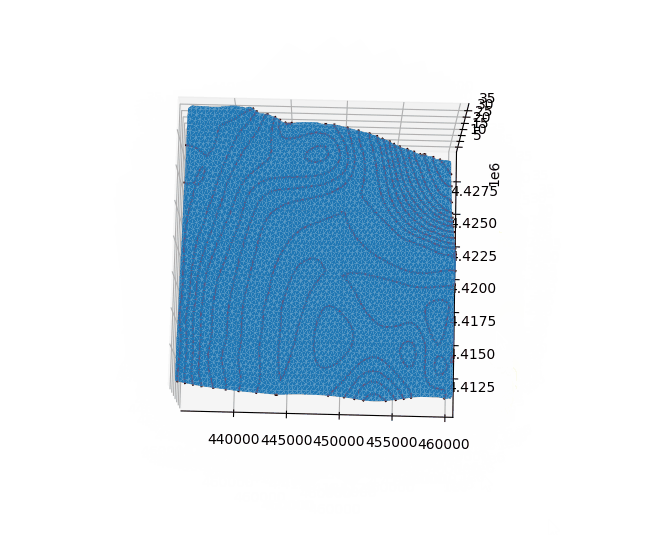
使用python绘制三角网以及等高线如下图所示,结果正常。
# pip install matplotlib
# file: test.py
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
from tin import Tin
# 参数准备:stl文件路径以及等高线的z间隔
path = "test.stl"
z_interval = 2
# 构建Tin类
obj = Tin()
# 读取stl文件中的三角网数据
obj.init_from_stl(path)
# 根据z间隔计算等高线
contour = obj.generate_contour(z_interval)
# 获取包围盒(绘制的时候用于控制显示范围)
box = obj.get_box()
# 获取用于绘制三角网数据
triangles = obj.get_tin()
# 初始化三维绘制视图
fig = plt.figure()
# ax = fig.gca(projection="3d")
ax = fig.add_subplot(projection="3d")
# 绘制三角网
ax.add_collection(Poly3DCollection(triangles))
# 绘制等高线
for polyline in contour:
polyline_x = []
polyline_y = []
polyline_z = []
for point in polyline:
polyline_x.append(point[0])
polyline_y.append(point[1])
polyline_z.append(point[2])
ax.plot(polyline_x, polyline_y, polyline_z, color="red")
# 设置视图的视角范围
ax.set_xlim([box[0][0], box[1][0]])
ax.set_ylim([box[0][1], box[1][1]])
ax.set_zlim([box[0][2], box[1][2]])
# 显示视图
plt.show()



























 2043
2043

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










