白话清晰讲解softmax名字的由来，适合想搞清神经网络本质的学者--神经网络之softmax(2)

转载https://blog.csdn.net/yangwohenmai1/article/details/95936462

通过对本系列的学习，你可以全面的了解softmax的来龙去脉。如果你尚不了解神经网络，通过本系列的学习，你也可以学到神经网络反向传播的基本原理。学完本系列，基本神经网络原理就算式入门了，毕竟神经网络基本的网络类型就那几种，很多变种，有一通百通的特点。

网上对softmax或是神经网络反向传播知识的整理，基本都通过一个长篇大论堆积出来，一套下来面面俱到但又都不精细。本文将每个环节拆开，分别进行详细介绍，即清晰易懂，又减轻了阅读负担，增加可读性。本文也借鉴了其他作者的内容，并列举引用，希望大家在学习过程中能有所收获

本章内容提要：

上一章我们了解了softmax函数的数学推导过程，知道了softmax的表达式为什么长得是这个样子。

本章我们首先从代数表达式的角度上，介绍softmax的演化过程。而后，从几何角度上介绍softmax图形所具有的特点和优点。帮你更好的理解softmax函数的特性。

本章算是softmax的拓展内容，看了之后可以更深刻的理解softmax函数，可以选看。

一、softmax函数回顾

通过对softmax前世今生系(1)的学习，我们知道了softmax的表达式：

                                                                                

而下面我们要介绍的softmax“暂时”长相和它有些不一样：

                                                                                

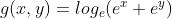
二者看起来完全不一样，但好像又有点关系的感觉，好像都是e的指数表达式。梅开两朵，各表一枝，他们的相关性我们暂时放下不谈，我们先聊聊g(x, y)这个函数的来源。

二、hardmax的特性

softmax函数其实是从hardmax演变而来的，hardmax函数其实是我们生活中很常见的一种函数，表达式是：

                                                                                 

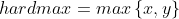
表达的意思很清楚，从写，y和x中取较大的那个值，为了方便后续比较，我们将hardmax的形式换一下：

                                                                                 

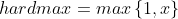
此时，函数本质功能没变，我们只是对定义域做了一个限制，即：

                                                                               

其图形如下：

                                                              

很显然这个函数在 x = 1 处是连续不可导的，可导能帮我们做很多事，那我们有没有办法对他变形，找到一个连续可导的近似函数？

三、softmax和hardmax的相似性

此时就有了softmax函数：

                                                                                 

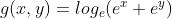
我们先来看一下这个代数表达式的数学特性。指数函数有一个特点，就是变化率非常快。当x>y时，通过指数的放大作用，会使得二者差距进一步变大，即：

                                                                                         

所以有：

                                                                                        

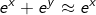
所以g(x，y)表达式有：

                                                                                 

                                                                                 

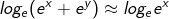
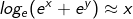
因此根据上面的推导过程，g(x，y)约等于x，y中较大的值，即：

                                                                                 

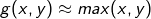
所以我们得出一个结论，g(x，y)是max{x，y}的近似函数，两个函数有相似的数学特性。我们再来看一下softmax函数的图像：

                                                         

很显然这是一个连续且处处可导的函数，这是一个非常重要的特性，g(x，y)即具有与max{x，y}的相似性，又避免了max{x，y}函数不可导的缺点。

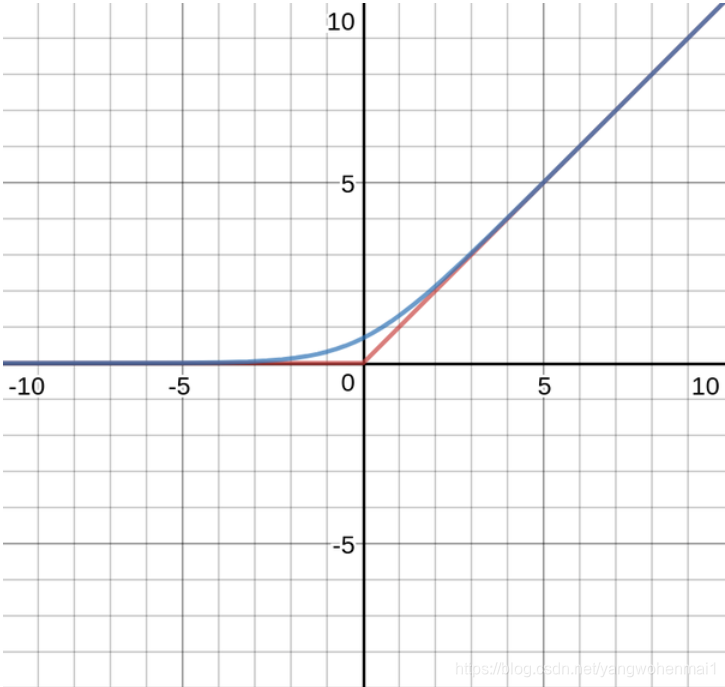
我们把两张图叠加到一起来看看，红色的折线是hardmax函数，他有一个尖尖的棱角，看起来很"hard"。蓝色的弧线看起来就平滑的多，不那么"hard"，这就是softmax函数了。这就时softmax函数名称的由来。

从图上可以看出，当x，y的差别越大时，softmax和hardmax函数吻合度越高。

 

                                                      

 

四、softmax函数概率模型构建

那么回到最初的问题，这个softmax函数和我们神经网络里面做分类层的softmax函数有什么关系呢？

假设我们要从a，b两个未知数字中取一个较大的值，即max{a，b}，那么取到两个数字的概率分别是多少呢？我们可以建立一个概率模型：

1.当a = b的时候，取a，b任意一个数字都可以，所以，取a或者取b的概率各50%。

                                                                              

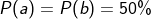
2.当a = 4，b = 6的时候，b比a更大，因此我们更倾向于取b，那么我们取到b的概率应该会更大一点

                                                                             

                                                                             

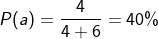
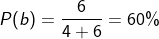
3.当a = 8，b = 2的时候，a比b更大，因此我们更倾向于取a，那么我们取到a的概率应该会更大一点

                                                                             

                                                                             

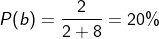
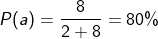
当变量变多时，hardmax就变成了max{s1，s2，s3，s4，...sn}，此时根据我们假设的概率模型，取到每一个样本点的概率就是：

                                                                           

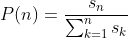
这个的表达式是不是很眼熟？

对于神经网络来说，训练的过程中处理损失调整权重矩阵的时候，需要用到求导。在第二部分我们已经了解到，hardmax函数并不是处处可导的，那么此时就用hardmax的近似函数softmax来代替他，我们已知二者表达式之间的关系：

                                                                       

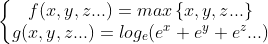
因此，根据hardmax函数的表达式，得出softmax的概率模型表达式：

                                                                        

以上就是softmax函数的由来，softmax函数是hardmax函数的近似函数，也是对hardmax函数的优化。解决了hardmax函数不可导的问题。因此被广泛的应用在神经网络中。

 

五、总结

文后的笔记中还讨论了softmax在计算中的一些优化方法，后续会单独总结一下。目前重点还是放在对softmax函数特性的分析上。

现在我们已经知道softmax函数的原理和数学上的特性，那么为什么softmax函数可以用在神经网络中，对计算结果进行分类呢？下篇文章我们将介绍softmax函数在神经网络中进行多分类的原理。

传送门：神经网络中的softmax层为何可以解决分类问题——softmax前世今生系列(3)

 

六、附学习笔记如下：

 

参考文献：https://blog.csdn.net/u010127033/article/details/82938888