设一元线性回归方程为![]() ,数据样本点为
,数据样本点为![]() ,
,
要想使这n个样本点落在一元线性回归方程附近,不妨设误差为![]() ,使得没一个样本点落在一元线性回归方程上,因此有
,使得没一个样本点落在一元线性回归方程上,因此有 恒成立,所以回归直线应满足的条件是:实际值与回归估计值之间的误差平方和最小,即:
恒成立,所以回归直线应满足的条件是:实际值与回归估计值之间的误差平方和最小,即:

此时令![]() ,原问题就转换成求解二元函数极小值问题,分别对
,原问题就转换成求解二元函数极小值问题,分别对![]() 求偏导:
求偏导:

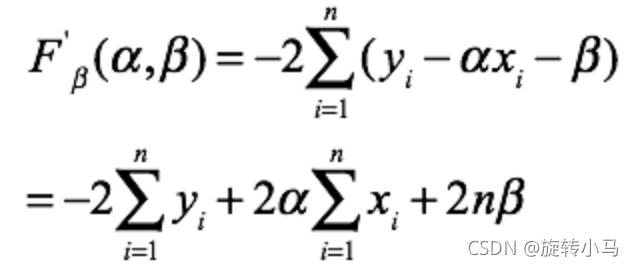
令上两式等于零,即

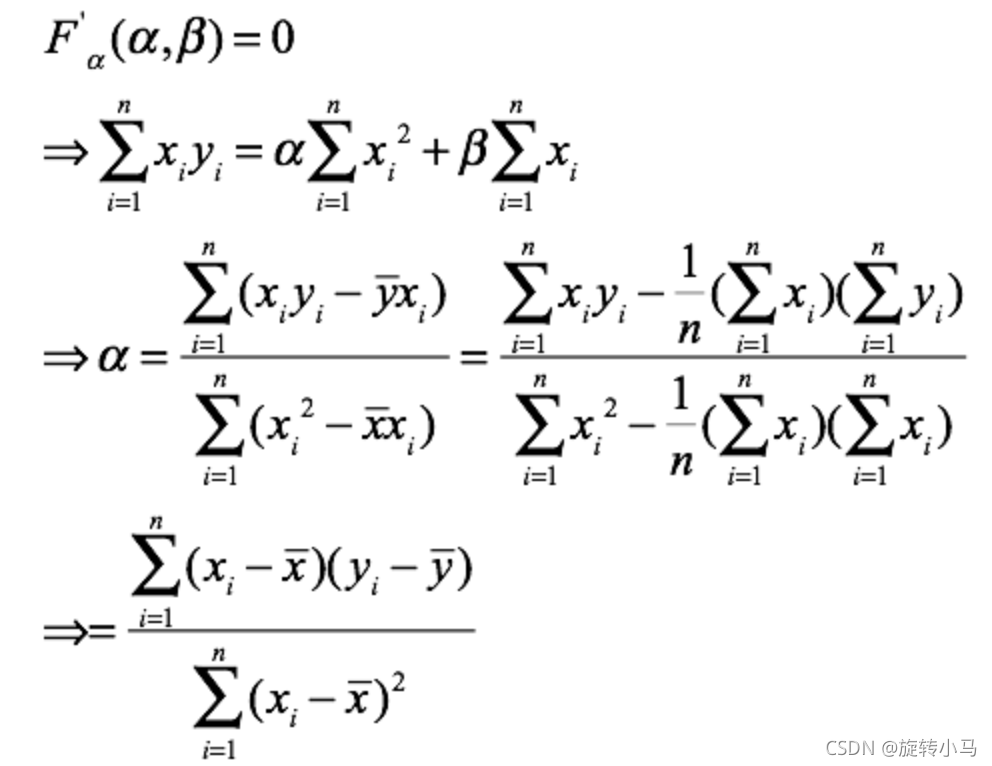
最终求出两个数值,一元线性回归方程也就拟合出来了。
设一元线性回归方程为![]() ,数据样本点为
,数据样本点为![]() ,
,
要想使这n个样本点落在一元线性回归方程附近,不妨设误差为![]() ,使得没一个样本点落在一元线性回归方程上,因此有
,使得没一个样本点落在一元线性回归方程上,因此有 恒成立,所以回归直线应满足的条件是:实际值与回归估计值之间的误差平方和最小,即:
恒成立,所以回归直线应满足的条件是:实际值与回归估计值之间的误差平方和最小,即:

此时令![]() ,原问题就转换成求解二元函数极小值问题,分别对
,原问题就转换成求解二元函数极小值问题,分别对![]() 求偏导:
求偏导:

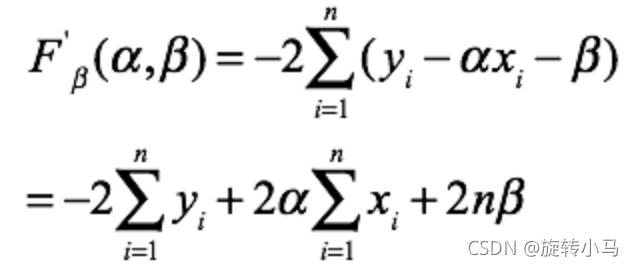
令上两式等于零,即

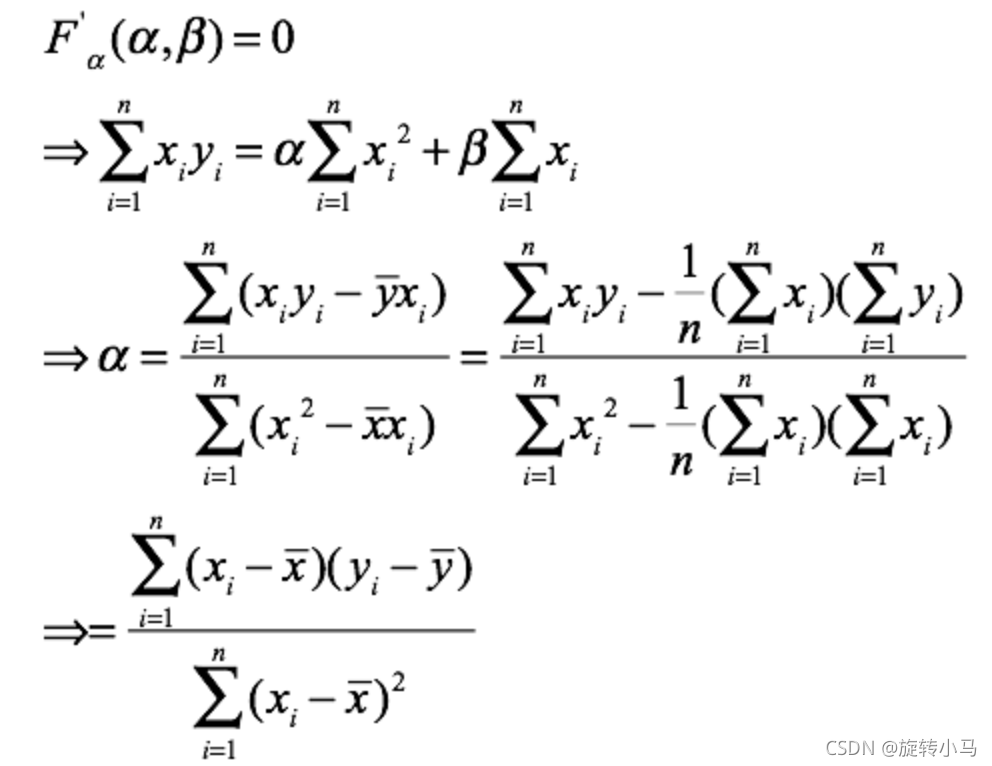
最终求出两个数值,一元线性回归方程也就拟合出来了。
 1608
1608
 8967
8967

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


