LeetCode Weekly Contest 37解题思路

LeetCode Weekly Contest 37解题思路

详细代码可以fork下Github上leetcode项目，不定期更新。

赛题

本次周赛主要分为以下4道题：

• Leetcode 624. Maximum Distance in Arrays
• Leetcode 623. Add One Row to Tree
• Leetcode 625. Minimum Factorization
• Leetcode 621. Task Scheduler

Leetcode 624. Maximum Distance in Arrays

Problem:

Given m arrays, and each array is sorted in ascending order. Now you can pick up two integers from two different arrays (each array picks one) and calculate the distance. We define the distance between two integers a and b to be their absolute difference |a-b|. Your task is to find the maximum distance.

Example 1:

Input:
[[1,2,3],
[4,5],
[1,2,3]]
Output: 4
Explanation:
One way to reach the maximum distance 4 is to pick 1 in the first or third array and pick 5 in the second array.

Note:

• Each given array will have at least 1 number. There will be at least two non-empty arrays.
• The total number of the integers in all the m arrays will be in the range of [2, 10000].
• The integers in the m arrays will be in the range of [-10000, 10000].

思路：

• 把每一行的最大值放入一个数组中，对其排序，得到一个降序排列的max集合。
• 遍历每一行，取每一行的最小值，更新ans，如果最大值在当前行，则取次大的。

代码如下：

class Pair{
        int index;
        int value;
        Pair(int index, int value){
            this.index = index;
            this.value = value;
        }
    }

    public int maxDistance(int[][] arrays) {
        if (arrays == null || arrays.length == 0) return 0;
        int row = arrays.length;
        Pair[] p = new Pair[row];
        for (int i = 0; i < row; ++i){
            p[i] = new Pair(i,arrays[i][arrays[i].length - 1]);
        }
        Arrays.sort(p,(a,b) -> b.value - a.value);
        int max = 0;
        for (int i = 0; i < row; ++i){
            int x = arrays[i][0];
            int c = p[0].index != i ? p[0].value : p[1].value;
            max = Math.max(max, Math.abs(c - x));
        }
        return max;
    }

比较容易理解和直观的做法，但时间复杂度为$O(n \log n)$，这道题有$O(n)$的做法。

在遍历每一行时，我们都会有一行里的最大和最小元素，遍历的同时，不断更新min和max的最值，在下一行，用当前的最小减最大，最大减最小，也能得到正确答案，且复杂度为$O(n)$，这种做法不再需要判断当前所在的行数。

public int maxDistance(int[][] arrays) {
        if (arrays == null || arrays.length == 0) return 0;
        int min = arrays[0][0];
        int max = arrays[0][arrays[0].length-1];

        int diff = 0;
        for (int i = 1; i < arrays.length; ++i){
            int head = arrays[i][0];
            int tail = arrays[i][arrays[i].length - 1];
            diff = Math.max(diff, Math.abs(max - head));
            diff = Math.max(diff, Math.abs(tail - min));
            max = Math.max(max, tail);
            min = Math.min(min, head);
        }
        return diff;
    }

吼吼，说实话，这道题要理解其精髓要思考一会，首先，我的第一版本是$O(n\log n)$，但在写的时候，我就有一种意识，每次操作的元素都是最大和次大的两个元素，这意味着这问题是可以reduce到$O(n)$的，直观来说，它们维护的貌似是全局信息。

第二个版本理解了很久，因为我不知道为什么要使用这种结构更新最终就能够得到正确值，比如：在更新当前行i时，难道就不需要考虑第i+1行后的元素么？这种遍历顺序不会影响答案？为什么不会？

后来，我才发现这种【交叉更新】的好处。

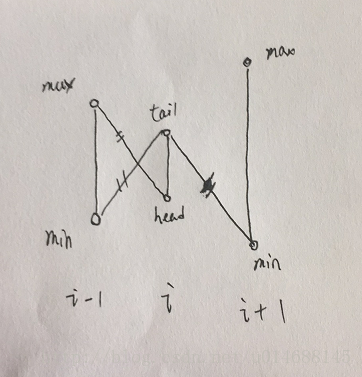
证明：（第二个版本），看图吧

当我遍历第i行时，当前的tail必须减去i-1行的最小和第i+1行的最小，这还不能导致正确答案，还忽略了第i-1行的max减去第i+1行的min，以及第i+1行的max减去第i-1行的最小。

它的比较次数是6次，嗯哼，但我们知道一个事实，我只要找到全局的最小min，然后让每个i-1和i和i+1减去全局的最小就是我们的答案，这也就是我的第一种做法，$O(n\log n)$.

那么交叉更新有什么好处呢？在上述更新过程中，我们需要考虑第i行后面的最小元素，交叉更新能够省略这种比较，高明。

证明一个结论：（第i行的元素没必要和第i+1行后的元素比较，而是只需考虑前i-1行的最小最大即可）

如果第i+1行的最大最小均小于全局的最大最小，容易看出一定得不到最大的diff。

如果第i+1行的最大最小大于全局的最大最小？那么我们知道：

tail - min{i+1} > tail - min{i}
head - max{i+1} > head - max{i}

所以可能最大的diff：
tail - min{i+1}和head - max{i+1}中的一个

此时，当遍历第i+1行时，我们可以得到当前可能的最大diff：
max{i+1} - min{i-1} > tail - min{i+1}
min{i+1} - max{i-1} > head - max{i+1}

综上：tail - min{i+1}和head - max{i+1} 的求解是冗余，即完全不需要考虑后方的元素，而是按照i递增的顺序更新即可。

直观上来看，我们可以把min-max和max-min看成整体，这样就好比求数组中的最大值一样，无非前者是“二维”的，而后者是“一维”的。

Leetcode 623. Add One Row to Tree

Problem:

Given the root of a binary tree, then value v and depth d, you need to add a row of nodes with value v at the given depth d. The root node is at depth 1.

The adding rule is: given a positive integer depth d, for each NOT null tree nodes N in depth d-1, create two tree nodes with value v as N’s left subtree root and right subtree root. And N’s original left subtree should be the left subtree of the new left subtree root, its original right subtree should be the right subtree of the new right subtree root. If depth d is 1 that means there is no depth d-1 at all, then create a tree node with value v as the new root of the whole original tree, and the original tree is the new root’s left subtree.

没东西，preOrder？whatever，只要标识当前结点是哪一层的，改写一些结点的left和right即可。

代码如下：

public TreeNode addOneRow(TreeNode root, int v, int d) {
        if (d == 1){
            TreeNode r = new TreeNode(v);
            r.left = root;
            return r;
        }
        dfs(root,v,d,1);
        return root;
    }

    private void dfs(TreeNode root, int v, int d, int layer) {
        if (root == null)
            return;

        if (layer == d - 1){
            TreeNode left = root.left;
            TreeNode right = root.right;
            root.left = new TreeNode(v);
            root.right = new TreeNode(v);
            root.left.left = left;
            root.right.right = right;
        }
        dfs(root.left, v, d, layer + 1);
        dfs(root.right, v, d, layer + 1);
    }

Leetcode 625. Minimum Factorization

Problem:

Given a positive integer a, find the smallest positive integer b whose multiplication of each digit equals to a.

If there is no answer or the answer is not fit in 32-bit signed integer, then return 0.

Example:

Input:

48
Output:
68

Input:

15
Output:
35

思路：
算是贪心？最小的满足条件的b，最小是关键，而且是digit，这就意味着只能从1-9中挑，先挑最大的，这样能够保证b一定是最小的。最后把求得的digit排个序，输出。

也算是个递归子问题。

代码如下：

public int smallestFactorization(int a) {
        if (a < 9) return a;
        String ans = "";
        while (a > 9){
            int i = 9;
            for (; i >= 1; --i){
                if (a % i == 0){
                    ans += i;
                    break;
                }
            }
            if (i == 1){ 
                return 0;
            }
            a = a / i;
        }
        ans += a;
        char[] array = ans.toCharArray();
        Arrays.sort(array);
        String small = new String(array);
        try {
            int num = Integer.parseInt(small);
            return num;
        } catch (NumberFormatException e) {
            return 0;
        }
    }

不需要排序，就是从最大的挑起，逆序输出就好了，也不一定要用String去拼接，多此一举。

简化版：

public int smallestFactorization(int a) {
        if (a < 9) return a;
        int[] res = new int[32];
        int j = 0;
        while (a > 9){
            int i = 9;
            for (; i >= 1; --i){
                if (a % i == 0){
                    res[j++] = i;
                    break;
                }
            }
            if (i == 1){ 
                return 0;
            }
            a = a / i;
        }
        res[j] = a;
        long ans = 0;
        while (j >= 0){
            ans = 10 * ans + res[j--];
            if (ans > Integer.MAX_VALUE) return 0;
        }
        return (int)ans;
    }

上述代码还能优化，除过的因子没必要重新再遍历一遍，所以解法如下：

public int smallestFactorization(int a) {
        if (a < 10) return a;
        int[] res = new int[32];

        int j = 0;
        for (int i = 9; i >= 2; --i){
            while (a % i == 0){
                res[j++] = i;
                a = a / i;
            }
        }
        if (a != 1) return 0;
        long ans = 0;
        for (int i = j - 1; i >= 0; --i){
            ans = 10 * ans + res[i];
            if (ans > Integer.MAX_VALUE) return 0;
        }
        return (int)ans;
    }

直观易懂，完美。

Leetcode 621. Task Scheduler

Problem:

Given a char array representing tasks CPU need to do. It contains capital letters A to Z where different letters represent different tasks.Tasks could be done without original order. Each task could be done in one interval. For each interval, CPU could finish one task or just be idle.

However, there is a non-negative cooling interval n that means between two same tasks, there must be at least n intervals that CPU are doing different tasks or just be idle.

You need to return the least number of intervals the CPU will take to finish all the given tasks.

Example :

Input: tasks = [‘A’,’A’,’A’,’B’,’B’,’B’], n = 2
Output: 8
Explanation: A -> B -> idle -> A -> B -> idle -> A -> B.

Note:

• The number of tasks is in the range [1, 10000].

呵呵，还是一道数学题，刚开始的想法居然是贪心+二分查找，自己想多了，贪心给任务分配位置的时候，如果能够计算得到某个长度，就没必要再二分多此一举了。

关键问题在于如何选择位置！起初的想法是统计任务出现的频次，高频的最先分配，分配时以间隔为n进行，而分配完最高频次的任务，再从头分配剩余空间和次高任务频次。

eg:
A A A A B B B C C  n = 1

假设有10个位置：
o o o o o o o o o o
0 1 2 3 4 5 6 7 8 9

统计频次：
A = 4
B = 3
C = 2

分配A
A o A o A o A o o o

分配B
A B A B A B A o o o

分配C
A B A B A B A C o C

上述策略有问题：因为我们可以：
A B A C A B A B C o

所以最小长度是9而不是10

上述是举反例推翻自己的策略过程，但真正应该如何得到正确的答案呢？有一种做法，叫做模拟，尝试模拟这种任务分配的过程，进行位置计数，得到的答案自然是最终解。（只要分配策略正确。。。）

在上面的分析中，已经看出一些端倪来了，可以得到：

• 一定选择最高频次进行分配。（反证法，如果选择较低频次的任务分配，它的最小长度为【(频次 - 1) * (n + 1) + 1】，那么较高频次的任务是不可能被放在这个长度的数组内，所以数组长度至少是【(最大频次 - 1) * (n+1) + 1】），所以先分配最高频次咯。
• 其次，我们可以从模拟的角度来看，这也是长度不是最优的真正原因，第一条性质只是帮助我们筛选策略罢了，如果先选择较低频次的任务分配，那么在后续任务分配当中，最高频次的任务一定会留到最后分配，如果这样，因为没有其他任务占位，系统只能idle处理，白白浪费资源。

所以说，如果每次都选择频次最高的任务分配，可以尽可能多的选择较低频次的任务占位，而不是idle。而且它是一种动态的分配过程，最高频次的任务不一定一直是A。

代码如下：

    class Pair{
        char key;
        int freq;
        public Pair(char key, int freq){
            this.key = key;
            this.freq = freq;
        }
    }

    public int leastInterval(char[] tasks, int n) {
        Map<Character, Integer> map = new HashMap<>();
        for (int i = 0; i < tasks.length; ++i){
            map.put(tasks[i], map.getOrDefault(tasks[i], 0) + 1);
        }
        Queue<Pair> pq = new PriorityQueue<>((a,b) -> (b.freq - a.freq));
        for (char key : map.keySet()){
            pq.offer(new Pair(key, map.get(key)));
        }

        int cnt = 0;
        while (!pq.isEmpty()){
            int k = n + 1;
            List<Pair> tmp = new ArrayList<>();
            while (k != 0 && !pq.isEmpty()){
                Pair p = pq.poll();
                p.freq--;
                tmp.add(p);
                cnt++;
                k--;
            }

            for (Pair p : tmp){
                if (p.freq != 0){
                    pq.offer(p);
                }
            }
            if (pq.isEmpty()) break;
            cnt = cnt + k;
        }
        return cnt;
    }

模拟的做法比较容易理解，其实关键问题在于一个任务除了只认自身之外，对于其它任务来说，它们都是一样的。在A眼里，B和C没区别，所以B来占位还是C来占位无所谓，但A和A就必须保持在n间隔之外，这是策略精髓所在。

好了，有了上述的理解，就可以用数学的方法解决了。长度至少为【（最高频次-1）*（n+1） + 1】，利用性质：

A和A必须保持在n间隔之外

那么此时，如果长度已经超过了任务的长度，答案就是此长度，但需要注意最高频次相同的情况下，还需要多几个位置出来。

如果【（最高频次-1）*（n+1） + 1】小于任务长度，说明每个n间隔都可以被其它任务塞满，直接返回任务长度即可。这真不好想象，只能从模拟的做法当中证明它的正确性，因为每次都能被塞满，所以k始终为0，不存在idle状态，所以cnt自然是所有频次的总和，也就是总任务数。

代码如下：

    public int leastInterval(char[] tasks, int n) {
        int[] map = new int[26];

        for (int i = 0; i < tasks.length; ++i){
            map[tasks[i] - 'A']++;
        }
        Arrays.sort(map);
        int j = 25;
        while (j >= 0 && map[j] == map[25]) j--;
        return Math.max(tasks.length, (map[25] - 1) * (n + 1) + 25 - j);
    }