图

0、引入

在计算机科学领域中，图是最为灵活的数据结构之一。事实上，大多数其他的数据结构也都能表示为图的形式，尽管按照这种方式表示它们通常会变得更加复杂。一般来说，图在定义对象之间的关系或或联系这类问题上能够作为一种模型来帮助我们。图中的对象可能是某种实际的实体，比如网络中的结点或者河流中的岛屿，但这也并非必须如此。通常，对象都不是那么具体，比如说某个系统中的状态或数据库中的业务。相同点只是对象之间的关联和联系。网络中的结点是物理上相连接的，但系统中状态之间的关系可能只是简单地表示为了达到下一个状态在当前所做出的决策。无论是什么情况，图的模型都很有用，能够解决许多有趣的计算问题。在图中，对象由顶点表示，而对象之间的关系或关联则通过定点之间的边来表示。

1、图的描述

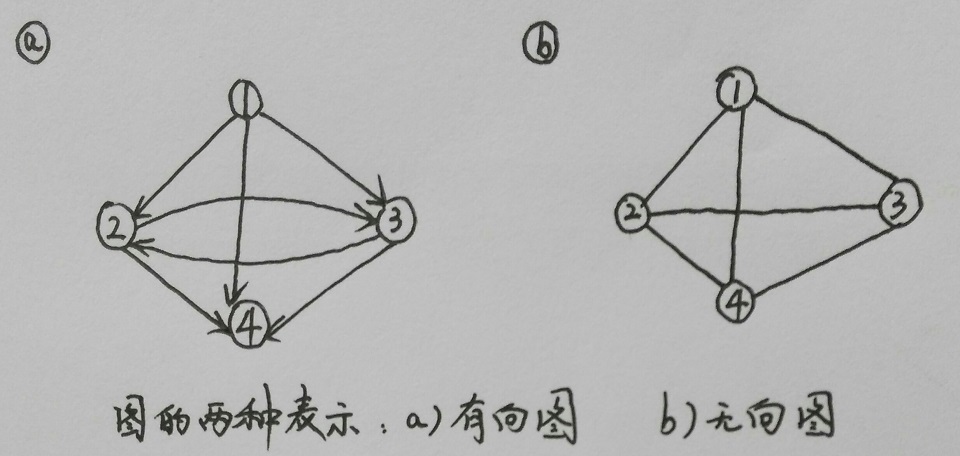
图由两种类型的元素组成：顶点和边。顶点代表对象，边则建立起对象之间的关系或关联。在许多问题中，图的边都关联了值或者权重的信息。图要么是有向的要么是无向的。在有向图中，边是由两个顶点组成的有序对，具有特定的方向。形象地说，有向图可以由顶点和带方向的箭头所组成的圈绘制出来。有时候，有向图的边也称为弧。在无向图中，边是没有方向的；因而，无向图的边就直接用线段来代替箭头表示。具体图示如下：

图的正式表示法是G=(V, E)，这里V代表顶点的集合，而E和V之间是一种二元关系。在有向图中，如果某条边是从顶点u开始到顶点v结束，则E包含有序对(u, v)。比如，在图a中，V={1, 2, 3, 4}，而E={(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 2), (3, 4)}。按照惯例，在图中表示边的集合时，用圆括号而不是大括号。在无向图中，由于边(u, v)和(v, u)是一样的意思，因此在E中只需要记录其中一个就可以了。因而，在图b中，V={1, 2, 3, 4}，而E={(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)}。在有向图中边可能会指回同一个顶点，但在无向图中则不会出现这种情况。

图中的两个重要关系是邻接(adjacency)和关联(incidence)。邻接是两个顶点之间的一种关系。如果有向图包含边(u, v)，则称顶点v与顶点u邻接。在无向图中，这也暗示了顶点u也与顶点v邻接。换句话说，在无向图中邻接关系是对称的。而在有向图中则并非如此。比如，在图a中，顶点2与顶点1相邻接，但顶点1并不与顶点2相邻接。另一方面，顶点2与顶点3则互为邻接。如果一幅图中的每一个顶点都与其他顶点相邻接，则称这幅图是完全图。

关联是指顶点和边之间的关系。在有向图中，边(u, v)从顶点u开始关联到v。因此，在图a中，边(1, 2)从顶点1开始关联到顶点2。在有向图中，顶点的入度(in-degree)指的是以该顶点为终点的边的数目。而顶点的出度(out-degree)指的是以该顶点为起点的边的数目。在无向图中，边(u, v)与顶点u和v相关联，而顶点的度就是与该顶点相关联的边的数目。

我们常常在图中说到路径。路径是依次遍历顶点序列之间的边所形成的轨迹。正式的说法是，顶点u到另一个顶点u'的路径由顶点序列<V0, V1, V2, ..., Vk>组成，使得u=V0且u'=Vk，对于i=1, 2, ..., k，所有的(Vi-1, Vi)均属于E。这样的一条路径包含边(V0, V1)，(V1, V2)，……，(Vk-1, Vk)，且长度为k。如果存在一条从u到u'的路径，则u'从u是可达的。没有重复顶点的路径称为简单路径。

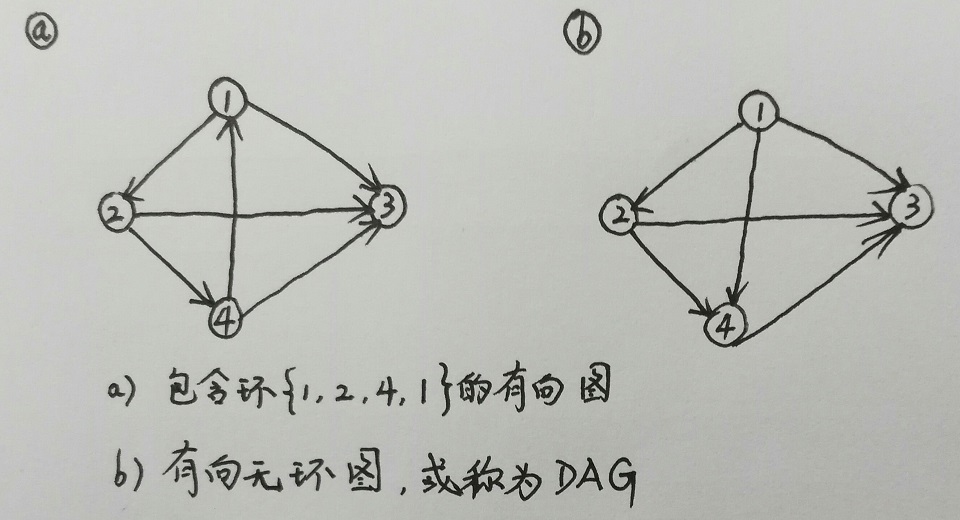
环是指路径包含相同的顶点两次或两次以上。也就是说，在有向图的一条路径中，如果从某个顶点出发，最后能够返回该顶点，则该路径是环。下图a包含环{1, 2, 4, 1}。正式的说法是，在有向图中，如果V0=Vk，且路径包含至少一条边，则该路径组成一个环。在无向图中，有路径<V0, V1, V2, ..., Vk>，如果V0=Vk且从V1到Vk中没有重复的顶点，则该路径组成一个环。没有环的图称为无环图，有向无环图有特殊的名称，叫做DAG(Directed Acyline Graph的缩写)(见下图b)。

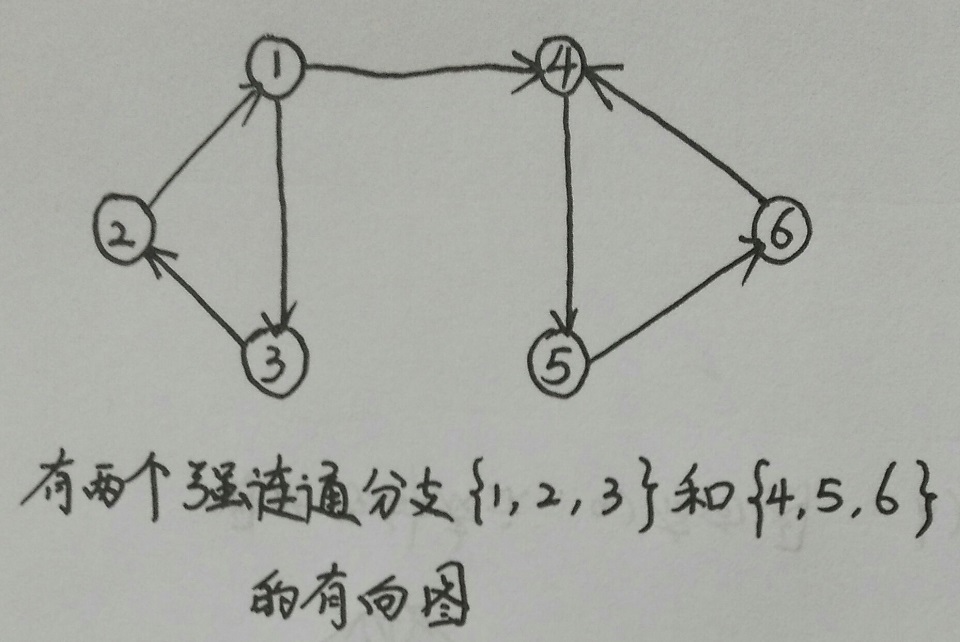
连通性是图中另一个重要的概念。对于无向图而言，如果它的顶点都能通过某条路径到达其他顶点，那么我们称它为联通的。如果该条件在有向图中同样成立，则称该图是强连通的。尽管无向图可能不是连通的，但它仍然可能包含连通的部分，这部分称为连通分支。如果有向图中只有部分是强连通的，则该部分称为强连通分支。(见下图)。

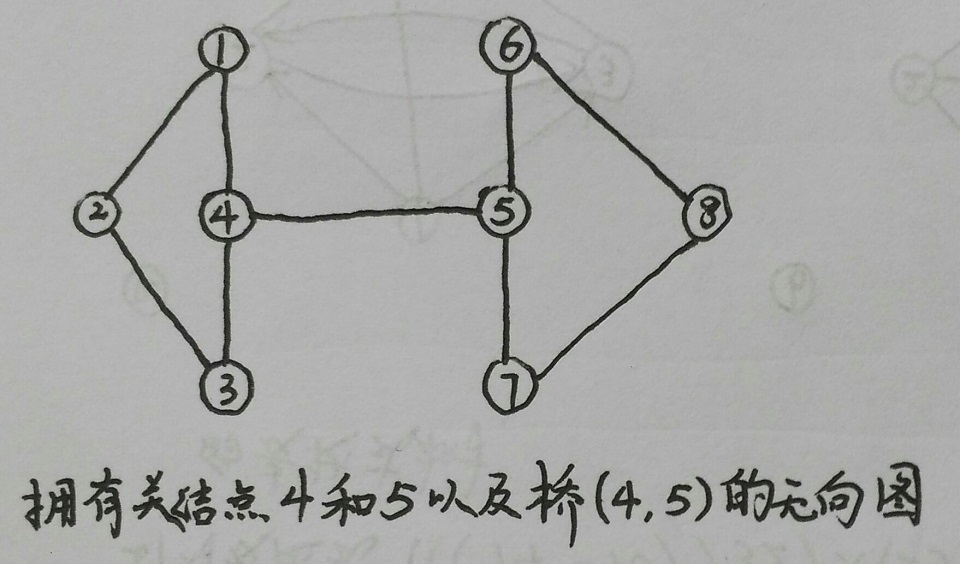
某些特定的顶点对于保持图或连通分支的连通性有特殊的重要意义。如果移除某个顶点将使得图或某分支失去连通性，则称该顶点为关结点。比如，在下图中，顶点4和5都是关结点，因为如果它们中的任意一个被移除，图就变成非连通的了。移除这些顶点后，图中拥有两个连通分支，{1, 2, 3}和{6, 7, 8}。如果移除某条边会使得图失去连通性，则称该边为桥。没有关结点的连通图称为双连通图。尽管图本身可能不是双连通的，但它仍然可能包含双连通分支。

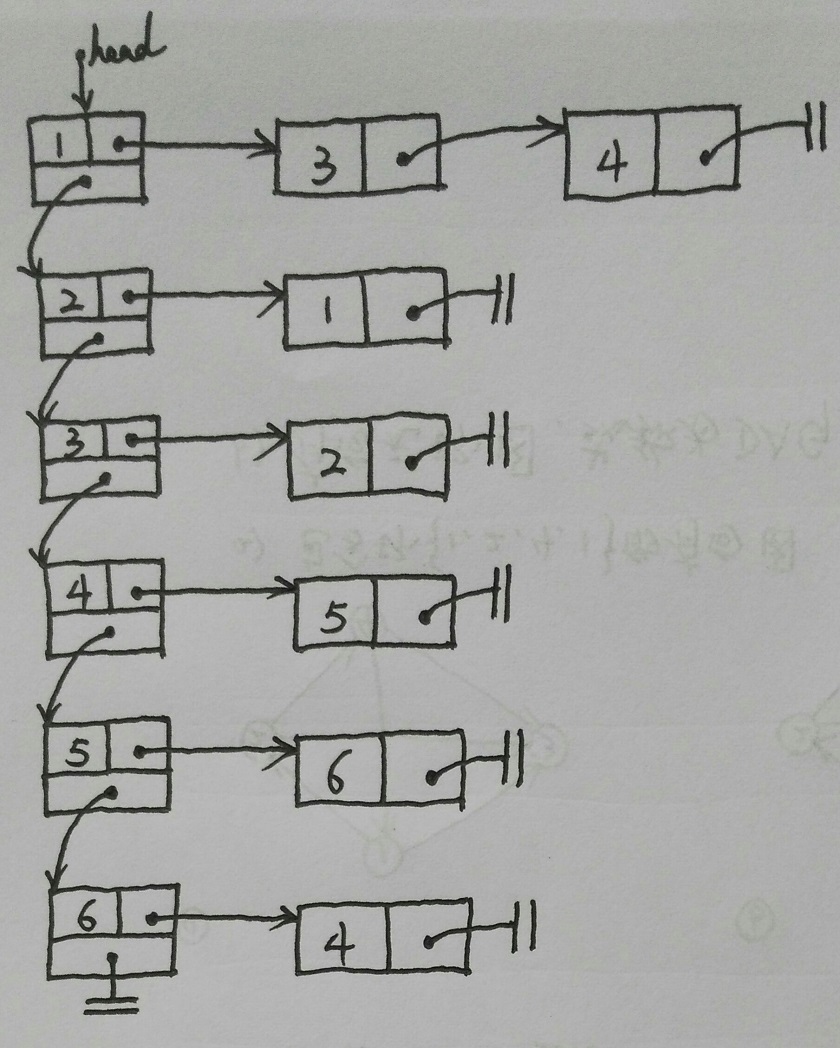
在计算机中，最常用来表示图的方法是采用邻接表表示形式，邻接表按照链表的方式组织起来。链表中的每个结构都包含两个成员：一个顶点和与该顶点邻接的顶点所组成的一个邻接表。如下图。

在图G=(V, E)中，如果V中的两个顶点u和v组成E中的边(u, v)，则顶点v包含在顶点u的邻接表中。因而，在有向图中，所有邻接表中的顶点总数同总的边数相等。在无向图中，由于边(u, v)暗含了边(v, u)，因此顶点v包含在顶点u的邻接表中，而顶点u也包含在顶点v的邻接表中。因而，在这种情况下，所有邻接表中的顶点总数是总边数的两倍。

通常，邻接表多用于稀疏图中，稀疏图是指边数相对来说较少的图。稀疏图非常普遍，但是如果图是稠密型的，就应该选择采用邻接矩阵表示方式来表示稠密图了。邻接矩阵表示方式需要占用O(VE)的空间。

搜索方法

对一个图进行搜索意味着按照某种特定的顺序依次访问某顶点。有两种重要的搜索方法在很多图算法中都采用过：广度优先搜索和深度优先搜索。

广度优先搜索在进一步探索图中的顶点之前先访问当前顶点的所有邻接结点。

深度优先搜索在搜索过程中每当访问到某个顶点后，需要递归地访问此顶点的所有未访问过的相邻顶点。

2、图的接口定义

graph_init

——————

void graph_init(Graph *graph, int (*match)(const void *key1, const void *key2), void (*destroy)(void *data));

返回值：无

描述：初始化由参数graph所指定的图。该函数必须在执行其他与图相关的操作之前调用。match参数指定用来判断两个顶点是否匹配的函数，该函数会用在其他的图操作中。当key1等于key2时，match函数返回1；否则返回0。destroy参数所指定的函数提供一种释放动态分配数据空间的方法。比如，如果图包含通过malloc动态分配的空间，则destroy应该设置为free，当销毁图时以此来释放动态分配的内存。对于包含多个动态分配成员的结构化数据，destroy参数应该设置为一个用户定义的析构函数，用来对每一个动态分配的成员以及结构体自身做资源回收操作。如果图包含不需要动态释放空间的数据，destroy参数应该设置为NULL。

复杂度：O(1)

graph_destroy

——————

void graph_destroy(Graph *graph);

返回值：无

描述：销毁由参数graph所指定的图。该函数调用后，任何其他的图操作都不允许再执行，除非用户再次调用graph_init。graph_destroy操作将图中所有的顶点和边都移除，如果destroy参数不为NULL的话，则调用destroy参数所指定的析构函数针对每个移除的顶点和边做资源回收操作。

复杂度：O(V+E)，这里V是图中顶点的个数，E是边的个数。

graph_ins_vertex

——————

int graph_ins_vertex(Graph *graph, const void *data);

返回值：如果插入结点成功，返回0；如果顶点已经存在，返回1；否则返回-1。

描述：将顶点插入由参数graph所指定的图中。新顶点包含一个指向data的指针，因此只要顶点还在图中，data所引用的内存就必须保持有效。由调用者负责管理data所引用的存储空间。

复杂度：O(V)，这里V代表图中的顶点个数。

graph_ins_edge

——————

int graph_ins_edge(Graph *graph, const void *data1, const void *data2);

返回值：如果插入操作成功，返回0；如果边已经存在，返回1；否则返回-1。

描述：将由data1以及data2所指定的顶点构成的边插入图中。data1和data2必须是使用graph_ins_vertex已经插入图中的顶点。新的边由data1所指定的顶点的邻接表中指向data2的指针来表示。因此，只要这条边还在图中，data2所引用的内存就必须保持合法。由调用者负责维护data2所引用的内存空间。要在无向图中插入边(u, v)，需要调用该函数两次：第一次将插入由u到v的边，第二次插入由v到u的边。这种类型的表示法对于无向图来说很普遍。

复杂度：O(V)，这里V代表图中的顶点数量。

graph_rem_vertex

——————

int graph_rem_vertex(Graph *graph, void **data);

返回值：如果移除顶点成功，返回0；否则返回-1。

描述：从graph指定的图中移除与data相匹配的顶点。在调用该函数前，所有与该顶点相关的边都必须移除。函数返回后，data指向已移除顶点中保存的数据。由调用者负责管理data所引用的存储空间。

复杂度：O(V+E)，这里V代表图中的顶点个数，而E代表边的个数。

graph_rem_edge

——————

int graph_rem_edge(Graph *graph, void *data1, void **data2);

返回值：如果移除成功，返回0；否则返回-1。

描述：从graph指定的图中移除从data1到data2的边。函数返回后，data2指向由data1所指定的顶点的邻接表中保存的数据。由调用者负责管理data2所引用的存储空间。

复杂度：O(V)，这里V代表图中顶点的个数。

graph_adjlist

——————

int graph_adjlist(const Graph *graph, const void *data, AdjList **adjlist);

返回值：如果取得邻接表成功，返回0；否则返回-1。

描述：取出graph中由data所指定的顶点的邻接表。返回的邻接表以结构体AdjList的形式保存，该结构体包含与data相匹配的顶点，以及其他与其邻接的顶点。函数返回后得到一个指向邻接表的指针，因此调用者必须保证不修改邻接表中的数据，否则将破坏原始图中的数据。

复杂度：O(V)，这里V代表图中顶点的个数。

graph_is_adjacent

——————

int graph_is_adjacent(const Graph *graph, const void *data1, const void *data2);

返回值：如果第二个顶点与第一个顶点邻接，返回1；否则返回0。

描述：判断由data2所指定的顶点是否与graph中由data1所指定的顶点邻接。

复杂度：O(V)，这里V代表图中的顶点个数。

graph_adjlists

——————

List graph_adjlists(const Graph *graph);

返回值：由邻接表结构所组成的链表。

描述：这是一个宏，用来返回由参数graph所指定的图中的邻接表结构链表。该链表中的每一个元素都是一个AdjList结构体。由于返回的是图中的邻接表结构链表而不是其拷贝，因此用户必须保证不对该链表做其他操作。

复杂度：O(1)

graph_vcount

——————

int graph_vcount(const Graph *graph);

返回值：图中顶点的个数。

描述：这是一个宏，用来计算graph指定的图中顶点的个数。

复杂度：O(1)

graph_ecount

——————

int graph_ecount(const Graph *graph);

返回值：图中边的个数。

描述：这是一个宏，用来计算graph指定的图中边的个数。

复杂度：O(1)

3、图的实现与分析

我们主要通过邻接表链表结构来表示图。链表中的每个结构体都包含两个成员：一个顶点以及与该顶点相邻接的一个顶点集合。实现时，邻接表链表中的结点由结构体AdjList表示。该结构体包含前面刚提到的两个成员。每个顶点的邻接表实现为一个集合(之前博文有讲到)。结构体Graph代表图这种数据结构。这个结构体由5个成员组成：vcount代表图中顶点的个数，ecount代表图中边的个数，match和destroy用来封装初始化时传给graph_init的函数，adjlists则代表邻接表链表。示例代码也为顶点的颜色属性定义了枚举类型，这些颜色属性在图的操作中需要经常用到。

// 图抽象数据类型的头文件

/* graph.h */

#ifndef GRAPH_H
#define GRAPH_H

#include <stdlib.h>

#include "list.h"
#include "set.h"

/* Define a structure for adjacency lists. */
typedef struct AdjList_
{
    void *vertex;
    Set adjacent;
} AdjList;

/* Define a structure for graphs. */
typedef struct Graph_
{
    int vcount;
    int ecount;
    int (*match)(const void *key1, const void *key2);
    void (*destroy)(void *data);
    List adjlists;
} Graph;

/* Define colors for vertices in graphs. */
typedef enum VertexColor_ {white, gray, black} VertexColor;

/* Public Interface */
void graph_init(Graph *graph, int (*match)(const void *key1, const void *key2), void (*destroy)(void *data));
void graph_destroy(Graph *graph);
int graph_ins_vertex(Graph *graph, const void *data);
int graph_ins_edge(Graph *graph, const void *data1, const void *data2);
int graph_rem_vertex(Graph *graph, void **data);
int graph_rem_edge(Graph *graph, void *data1, void **data2);
int graph_adjlist(const Graph *graph, const void *data, AdjList **adjlist);
int graph_is_adjacent(const Graph *graph, const void *data1, const void *data2);
#define graph_adjlists(graph) ((graph)->adjlists)
#define graph_cvount(graph) ((graph)->vcount)
#define graph_ecount(graph) ((graph)->ecount)

#endif // GRAPH_H

// 抽象数据类型图的实现

/* graph.c */

#include <stdlib.h>
#include <string.h>

#include "graph.h"
#include "list.h"
#include "set.h"

/* graph_init */
void graph_init(Graph *graph, int (*match)(const void *key1, const void *key2), void (*destroy)(void *data))
{
    /* Initialize the graph. */
    graph->vcount = 0;
    graph->ecount = 0;
    graph->match = match;
    graph->destroy = destroy;

    /* Initialize the list of adjacency-list structures. */
    list_init(&graph->adjlists, NULL);

    return;
}

/* graph_destroy */
void graph_destroy(Graph *graph)
{
    AdjList *adjlist;

    /* Remove each adjacency-list structure and destroy its adjacency list. */
    while(list_size(&graph->adjlists) > 0)
    {
        if(list_rem_next(&graph->adjlists, NULL, (void **)&adjlist) == 0)
        {
            set_destroy(&adjlist->adjacent);

            if(graph->destroy != NULL)
                graph->destroy(adjlist->vertex);

            free(adjlist);
        }
    }

    /* Destroy the list of adjacency-list structures, which is now empty. */
    list_destroy(&graph->adjlists);

    /* No operations are allowed now, but clear the structure as a precaution. */
    memset(graph, 0, sizeof(Graph));
    return;
}

/* graph_ins_vertex */
int graph_ins_vertex(Graph *graph, const void *data)
{
    ListElmt *element;
    AdjList *adjlist;
    int retval;

    /* Do not allow the insertion of duplicate vertices. */
    for(element = list_head(&graph->adjlists); element != NULL; element = list_next(element))
    {
        if(graph->match(data, ((AdjList *)list_data(element))->vertex))
            return 1;
    }

    /* Insert the vertex. */
    if((adjlist = (AdjList *)malloc(sizeof(AdjList))) == NULL)
        return -1;

    adjlist->vertex = (void *)data;
    set_init(&adjlist->adjacent, graph->match, NULL);

    if((retval = list_ins_next(&graph->adjlists, list_tail(&graph->adjlists), adjlist)) != 0)
    {
        return retval;
    }

    /* Adjust the vertex count to account for the inserted vertex. */
    graph->vcount++;
    return 0;
}

/* graph_ins_edge */
int graph_ins_edge(Graph *graph, const void *data1, const void *data2)
{
    ListElmt *element;
    int retval;

    /* Do not allow insertion of an edge without both its vertices in the graph. */
    for(element = list_head(&graph->adjlists); element != NULL; element = list_next(element))
    {
        if(graph->match(data2, ((AdjList *)list_data(element))->vertex))
            break;
    }

    if(element == NULL)
        return -1;

    for(element = list_head(&graph->adjlists); element != NULL; element = list_next(element))
    {
        if(graph->match(data1, ((AdjList *)list_data(element))->vertex))
            break;
    }

    if(element == NULL)
        return -1;

    /* Insert the second vertex into the adjacency list of the first vertex. */
    if((retval = set_insert(&((AdjList *)list_data(element))->adjacent, data2)) != 0)
    {
        return retval;
    }

    /* Adjust the edge count to account for the inserted edge. */
    graph->ecount++;
    return 0;
}

/* graph_rem_vertex */
int graph_rem_vertex(Graph *graph, void **data)
{
    ListElmt *element, *temp, *prev;
    AdjList *adjlist;
    int found;

    /* Traverse each adjacency list and the vertices it contains. */
    prev = NULL;
    found = 0;

    for(element = list_head(&graph->adjlists); element != NULL; element = list_next(element))
    {
        /* Do not allow removal of the vertex if it is in an adjacency list. */
        if(set_is_member(&((AdjList *)list_data(element))->adjacent, *data))
            return -1;

        /* Keep a pointer to the vertex to be removed. */
        if(graph->match(*data, ((AdjList *)list_data(element))->vertex))
        {
            temp = element;
            found = 1;
        }

        /* Keep a pointer to the vertex before the vertex to be removed. */
        if(!found)
            prev = element;
    }

    /* Return if the vertex was not found. */
    if(!found)
        return -1;

    /* Do not allow removal of the vertex if its adjacency list is not empty. */
    if(set_size(&((AdjList *)list_data(temp))->adjacent) > 0)
        return -1;

    /* Remove the vertex. */
    if(list_rem_next(&graph->adjlists, prev, (void **)&adjlist) != 0)
        return -1;

    /* Free the storage allocated by the abstract datatype. */
    *data = adjlist->vertex;
    free(adjlist);

    /* Adjust the vertex count to account for the removed vertex. */
    graph->vcount--;
    return 0;
}

/* graph_rem_edge */
int graph_rem_edge(Graph *graph, void *data1, void **data2)
{
    ListElmt *element;

    /* Locate the adjacency list for the first vertex. */
    for(element = list_head(&graph->adjlists); element != NULL; element = list_next(element))
    {
        if(graph->match(data1, ((AdjList *)list_data(element))->vertex))
            break;
    }

    if(element == NULL)
        return -1;

    /* Remove the second vertex from the adjacency list of the first vertex. */
    if(set_remove(&((AdjList *)list_data(element))->adjacent, data2) != 0)
        return -1;

    /* Adjust the edge count to account for the removed edge. */
    graph->ecount--;
    return 0;
}

/* graph_adjlist */
int graph_adjlist(const Graph *graph, const void *data, AdjList **adjlist)
{
    ListElmt *element, *prev;

    /* Locate the adjacency list for the vertex. */
    prev = NULL;
    for(element = list_head(&graph->adjlists); element != NULL; element = list_next(element))
    {
        if(graph->match(data, ((AdjList *)list_data(element))->vertex))
            break;

        prev = element;
    }

    /* Return if the vertex was not found. */
    if(element == NULL)
        return -1;

    /* Pass back the adjacency list for the vertex. */
    *adjlist = list_data(element);
    return 0;
}

/* graph_is_adjacent */
int graph_is_adjacent(const Graph *graph, const void *data1, const void *data2)
{
    ListElmt *element, *prev;

    /* Locate the adjacency list of the first vertex. */
    prev = NULL;

    for(element = list_head(&graph->adjlists); element != NULL; element = list_next(element))
    {
        if(graph->match(data1, ((AdjList *)list_data(element))->vertex))
            break;

        prev = element;
    }

    /* Return if the first vertex was not found. */
    if(element == NULL)
        return 0;

    /* Return whether the second vertex is in the adjacency list of the first. */
    return set_is_member(&((AdjList *)list_data(element))->adjacent, data2);
}

graph_init

graph_init函数用来初始化图，以便其他的操作能够执行。初始化图是一种简单的操作，我们将vcount和ecount成员设置为0，封装match和destroy所指定的函数，初始化邻接表链表结构。

graph_init的时间复杂度是O(1)，因为初始化图的所有步骤都能在恒定的时间内完成。

graph_destroy

graph_destroy函数用来销毁图。这表示要将每一个邻接表结构移除，销毁其中包含的顶点集合。当destroy参数不为NULL时，还需要调用destroy所指定的函数来释放分配给vertex成员的内存空间。

graph_destroy的时间复杂度为O(V+E)，这里V代表的是图中顶点的个数，而E代表边的个数。这是因为需要调用复杂度为O(1)的list_rem_next操作V次，而所有针对set_destroy的调用的总运行时间是O(E)。

graph_ins_vertex

graph_ins_vertex函数将一个顶点插入图中。具体的步骤是：该函数会将一个AdjList结构体插入邻接表链表结构中，并将AdjList结构体中的vertex成员指向由调用者传入的数据。首先，要确保该顶点不存在于列表中。之后，通过调用list_ins_next将AdjList结构体插入链表的尾部。最后，将图数据结构的vcount成员加1以更新图中的顶点个数。

graph_ins_vertex的时间复杂度是O(V)，这里V代表图中的顶点个数。这是因为在链表中查找顶点是否重复是一个O(V)的操作。list_ins_next的复杂度是O(1)。

graph_ins_edge

graph_ins_edge函数将一条边插入图中。为了插入由顶点data1到顶点data2所指定的边，将data2插入data1的邻接表中。首先，保证这两个顶点都存在于图中。之后，通过调用set_insert将data2所指定的顶点插入data1的邻接表中。如果这条边已经存在的话，set_insert会返回一个错误。最后，将图数据结构的ecount成员加1，以更新图中边的个数。

graph_ins_edge的时间复杂度为O(V)，这里V代表的是图中顶点的个数。这是因为搜索邻接表链表结构以及对set_insert的调用都是O(V)的操作。

graph_rem_vertex

graph_rem_vertex函数将一个顶点从图中移除。具体来讲，该函数将一个AdjList结构体从邻接表链表结构中移除。首先确保该顶点不存在于任何邻接表中，但顶点要存在于邻接表链表结构中，且该顶点的邻接表为空。之后，通过调用list_rem_next从邻接表链表中移除合适的AdjList结构体。最后，使图数据结构的vcount成员递减1，更新图中的顶点计数。

graph_rem_vertex的时间复杂度为O(V+E)，这里V代表图中顶点的个数，而E代表边的个数。这是因为检索每一个邻接表是复杂度为O(V+E)的操作，而检索邻接表链表结构是一个复杂度为O(V)的操作，调用list_rem_next是O(1)的操作。

graph_rem_edge

graph_rem_edge函数将一条边从图中移除。具体来讲，该函数将由data2所指定的顶点从data1所指定的顶点的邻接表中移除。首先确保第一个顶点要存在于图中。一旦经过验证，就通过调用set_remove来将data2所指定的顶点从data1所指定的顶点的邻接表中移除，从而实现移除这条边的功能。如果data2不在data1的邻接表中，则set_remove将返回一个错误。最后，通过递减图数据结构的ecount成员来更新图中的边的个数。

graph_rem_edge的时间复杂度为O(V)，这里V代表图中顶点的个数。这是因为搜索邻接表链表结构和调用set_remove的复杂度都是O(V)的。

graph_adjlist

graph_adjlist函数返回一个AdjList结构体，其中包含指定顶点的邻接顶点集合。为了实现这个操作，检索邻接表链表结构，直到找到其中包含指定顶点的那个AdjList结构体。

graph_adjlist操作的时间复杂度为O(V)，这里V代表图中顶点的个数。这是因为检索邻接表链表结构是复杂度为O(V)的操作。

graph_is_adjacent

graph_is_adjacent函数用来判断指定的顶点data1是否与另一个顶点data2有邻接关系。为了实现操作，首先在邻接表链表结构中定位由data1所指定的顶点，然后调用set_is_member来判断data2是否存在data1的邻接表中。

graph_is_adjacent的时间复杂度为O(V)，这里V代表图中顶点的个数。这是因为检索邻接表链表结构以及对set_is_member的调用都是复杂度为O(V)的操作。

graph_adjlists、graph_vcount、graph_ecount

这些宏实现了一些对图的简单操作。一般来说，这些宏提供了访问和测试结构体Graph中成员的接口。

这些宏的时间复杂度都是O(1)。因为访问结构体中成员的操作都能够在恒定的时间内完成。

4、关于图的应用举例：计算网络跳数

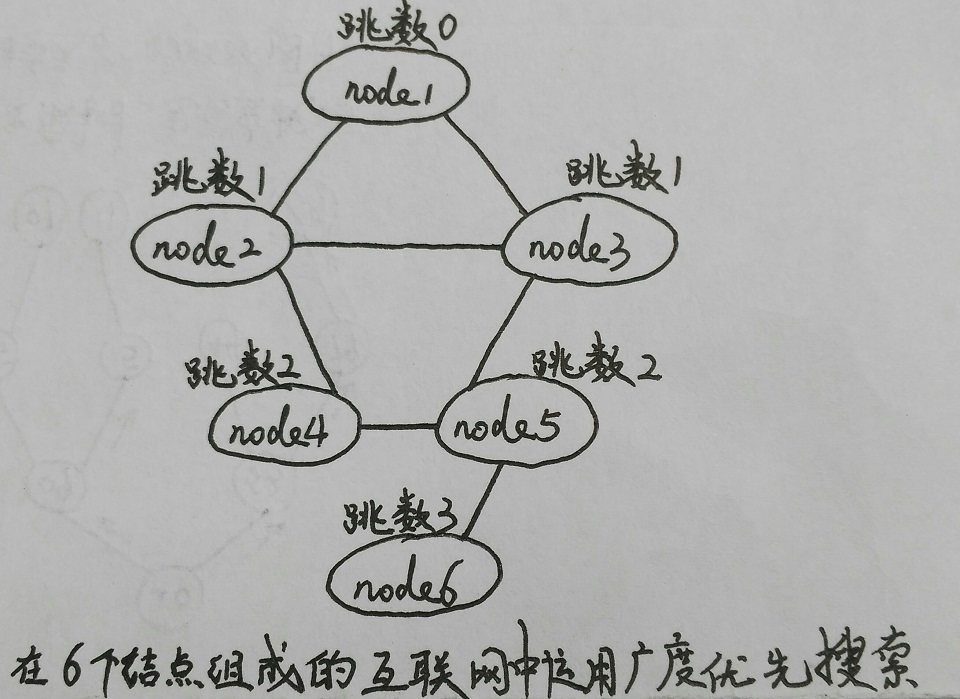
图在解决许多与网络相关的问题时起到了重要的作用。比如，其中一个问题：用来确定在互联网中从一个结点到另一个结点(一个网络到其他网络的网关)的最佳路径。一种建模方法是采用无向图，其中顶点表示网络结点，边代表结点之间的连接。通过这种模型，可以采用广度优先搜索来帮助确定结点间的最小跳数。

比如，考虑一下下图，改图代表Internet中的6个网络结点。以node1作为起点，有不止1条可以通往node4的路径。<node1, node2, node4>，<node1, node3, node2, node4>，以及<node1, node3, node5, node4>都是可行的路径。广度优先搜索可以确定最短的路径选择，即<node1, node2, node4>，一共只需要两跳。

本例给出了广度优先搜索的实现bfs。该函数用来确定互联网中两个结点之间的最小跳数。这个函数有3个参数：graph是一个图，在这个问题中就代表了整个网络；start代表起始的顶点；hops是返回的跳数链表。函数bfs会修改图graph，因此如果有必要的话需要在调用该函数之前先对图创建拷贝。另外，hops中返回的顶点是指向graph中实际顶点的指针，因此调用者必须保证只要访问hops，graph中的存储空间就必须保持有效。graph中的每个顶点都是一个BfsVertex类型的结构体，该结构体有3个成员：data是指向图中顶点的数据域的指针，color在搜索过程中维护顶点的颜色，hops维护从起始结点开始到其他顶点的跳数统计。match函数是由调用者在初始化graph时作为参数传给graph_init的。match应该只对BfsVertex结构体中的data成员进行比较。

bfs函数将按照前面介绍过的广度优先搜索的方式来计算。为了记录到达每个顶点的最小跳数，将每个顶点的hop计数设置为与该顶点邻接的顶点的hop计数加1。对于每个发现的顶点都这样处理，并将其着色为灰色。每个顶点的颜色和跳数信息都由邻接表结构链表中的BfsVertex来维护。最后，加载hops中所有跳数不为-1的顶点。这些就是从起始结点可到达的顶点。

bfs的时间复杂度为O(V+E)，这里V是图中顶点的个数，E是边的个数。这是因为初始化顶点的颜色属性以及确保起始结点存在都需要O(V)的运行时间，广度优先搜索中的循环的复杂度是O(V+E)，加载跳数统计链表的时间是O(V)。

// 广度优先搜索的头文件

/* bfs.h */

#ifndef BFS_H
#define BFS_H

#include "graph.h"
#include "list.h"

/* Define a structure for vertices in a breadth-first search. */
typedef struct BfsVertex_
{
    void *data;
    VertexColor color;
    int hops;
} BfsVertex;

/* Public Interface */
int bfs(Graph *graph, BfsVertex *start, List *hops);

#endif // BFS_H

// 广度优先搜索的实现

/* bfs.c */

#include <stdlib.h>

#include "bfs.h"
#include "graph.h"
#include "list.h"
#include "queue.h"

/* bfs */
int bfs(Graph *graph, BfsVertex *start, List *hops)
{
    Queue queue;
    AdjList *adjlist, *clr_adjlist;
    BfsVertex *clr_vertex, *adj_vertex;
    ListElmt *element, *member;

    /* Initialize all of the vertices in the graph. */
    for(element = list_head(&graph_adjlists(graph)); element != NULL; element = list_next(element))
    {
        clr_vertex = ((AdjList *)list_data(element))->vertex;
        if(graph->match(clr_vertex, start))
        {
            /* Initialize the start vertex. */
            clr_vertex->color = gray;
            clr_vertex->hops = 0;
        }
        else
        {
            /* Initialize vertices other than the start vertex. */
            clr_vertex->color = white;
            clr_vertex->hops = -1;
        }
    }

    /* Initialize the queue with the adjacency list of the start vertex. */
    queue_init(&queue, NULL);
    if(graph_adjlist(graph, start, &clr_adjlist) != 0)
    {
        queue_destroy(&queue);
        return -1;
    }

    if(queue_enqueue(&queue, clr_adjlist) != 0)
    {
        queue_destroy(&queue);
        return -1;
    }

    /* Perform breadth-first search. */
    while(queue_size(&queue) > 0)
    {
        adjlist = queue_peek(&queue);

        /* Traverse each vertex in the current adjacency list. */
        for(member = list_head(&adjlist->adjacent); member != NULL; member = list_next(member))
        {
            adj_vertex = list_data(member);

            /* Determine the color of the next adjacent vertex. */
            if(graph_adjlist(graph, adj_vertex, &clr_adjlist) != 0)
            {
                queue_destroy(&queue);
                return -1;
            }
            clr_vertex = clr_adjlist->vertex;

            /* Color each white vertex gray and enqueue its adjacency list. */
            if(clr_vertex->color == white)
            {
                clr_vertex->color = gray;
                clr_vertex->hops = ((BfsVertex *)adjlist->vertex)->hops + 1;

                if(queue_enqueue(&queue, clr_adjlist) != 0)
                {
                    queue_destroy(&queue);
                    return -1;
                }
            }
        }

        /* Dequeue the current adjacency list and color its vertex black. */
        if(queue_dequeue(&queue, (void **)&adjlist) == 0)
        {
            ((BfsVertex *)adjlist->vertex)->color = black;
        }
        else
        {
            queue_destroy(&queue);
            return -1;
        }
    }

    queue_destroy(&queue);

    /* Pass back the hop count for each vertex in a list. */
    list_init(hops, NULL);

    for(element = list_head(&graph_adjlists(graph)); element != NULL; element = list_next(element))
    {
        /* Skip vertices that were not visited (those with hop counts of -1). */
        clr_vertex = ((AdjList *)list_data(element))->vertex;

        if(clr_vertex->hops != -1)
        {
            if(list_ins_next(hops, list_tail(hops), clr_vertex) != 0)
            {
                list_destroy(hops);
                return -1;
            }
        }
    }

    return 0;
}

5、关于图的应用举例：拓扑排序

有些时候我们会遇到这一类问题：我们必须根据各种事件间的依赖关系来确定一种可接受的执行顺序。想象一下大学里那些需要满足一些先决条件才能选的课程，或者一个复杂的项目，其中某个特定的阶段必须在其他阶段开始之前完成。要为这一类问题建模，可以采用优先级图，其采用的是有向图的思想。在优先级图中，顶点代表任务，而边代表任务之间的依赖关系。要展示一个依赖关系，以必需先完成的任务为起始点，以依赖于此任务的其他任务为终点，画一条边即可。

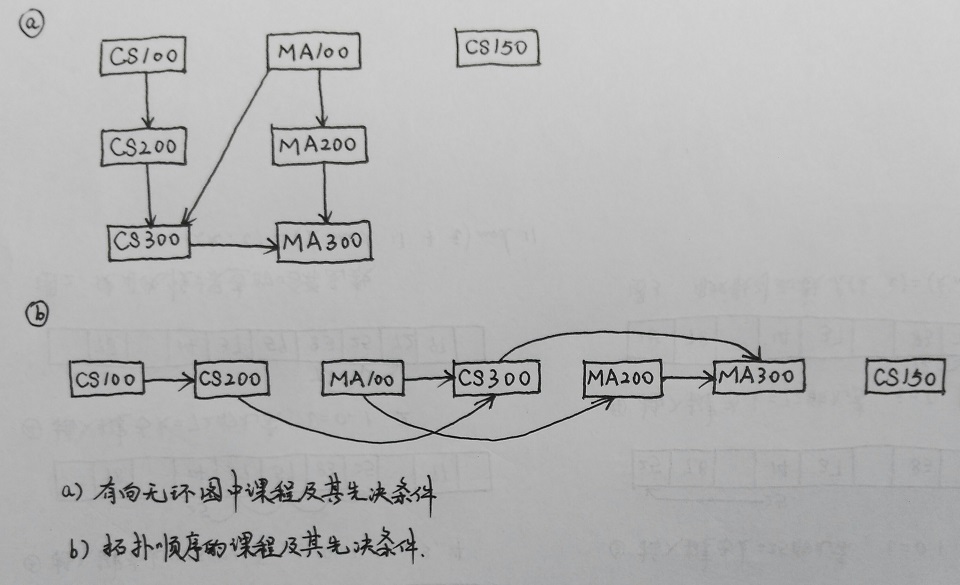
例如，考虑下图a中的有向无环图，它表示7门课程及其先决条件组成的一份课程表：CS100没有先决条件，CS200需要CS100，CS300需要CS200和MA100，MA100没有先决条件，MA200需要MA100，MA300需要CS300和MA200，并且CS150没有先决条件同时也不是先决条件。

通过对这些课程执行拓扑排序，深度优先搜索有助于确定出一种可接受的顺序。拓扑排序将顶点排列为有向无环图，因此所有的边都是从左到右的方向。在有关课程先决条件的问题中，这意味着所有满足先决条件的课程将出现在需要这种先决条件的课程的左边(见上图b)。正规来说，有向无环图G=(V, E)的拓扑排序是其顶点的一个线性排序，以便如果G中存在一条边(u, v)，那么在线性顺序中u出现在v前面，在许多情况下，满足此条件的顺序有多个。

该示例实现了函数dfs，即深度优先搜索。该函数在这里用来对任务做拓扑排序。dfs有两个参数：graph代表图，在这个问题中则代表需要排序的任务，而参数ordered是完成拓扑排序后返回的顶点链表。调用该函数会修改图graph，因此如果有必要的话，需要在调用前先对图graph创建一个副本。另外，函数返回后链表ordered中保存了指向图graph中顶点的指针，因此调用者必须保证，一旦访问ordered中的元素就必须保证graph中的存储空间保持有效。graph中的每一个顶点都是一个DfsVertex结构体，该结构体拥有两个成员：data是指向顶点数据域部分的指针，而color在搜索过程中负责维护顶点的颜色信息。match函数是由调用者在初始化graph时通过参数传递给graph_init的，该函数应该只对DfsVertex结构体中的data成员进行比较。

dfs函数按照之前介绍过的深度优先的方式进行搜索。dfs_main是实际执行搜索的函数。dfs中的最后一个循环保证对图中所有未相连的元素完成了检索。在dfs_main中逐个完成顶点的搜索并将其涂黑，然后插入链表ordered的头部。最后，ordered就包含完成拓扑排序后的顶点。

dfs的时间复杂度为O(V+E)，这里V代表图中顶点的个数，而E代表边的个数。这是因为初始化顶点的颜色需要O(V)的时间，而dfs_main的时间复杂度为O(V+E)。

// 深度优先搜索的头文件

/* dfs.h */

#ifndef DFS_H
#define DFS_H

/* Define a structure for vertices in a depth-first graph. */
typedef struct DfsVertex_
{
    void *data;
    VertexColor color;
} DfsVertex;

/* Public Interface */
int dfs(Graph *graph, List *ordered);

#endif // DFS_H

// 深度优先搜索的函数实现

/* dfs.c */

#include <stdlib.h>

#include "dfs.h"
#include "graph.h"
#include "list.h"

/* dfs_main */
static int dfs_main(Graph *graph, AdjList *adjlist, List *ordered)
{
    AdjList *clr_adjlist;
    DfsVertex *clr_vertex, *adj_vertex;
    ListElmt *member;

    /* Color the vertex gray and traverse its adjacency list. */
    ((DfsVertex *)adjlist->vertex)->color = gray;

    for(member = list_head(&adjlist->adjacent); member != NULL; member = list_next(member))
    {
        /* Determine the color of the next adjacent vertex. */
        adj_vertex = list_data(member);

        if(graph_adjlist(graph, adj_vertex, &clr_adjlist) != 0)
            return -1;

        clr_vertex = clr_adjlist->vertex;

        /* Move one vertex deeper when the next adjacent vertex is white. */
        if(clr_vertex->color == white)
        {
            if(dfs_main(graph, clr_adjlist, ordered) != 0)
                return -1;
        }
    }

    /* Color the current vertex black and make it first in the list. */
    ((DfsVertex *)adjlist->vertex)->color = black;

    if(list_ins_next(ordered, NULL, (DfsVertex *)adjlist->vertex) != 0)
        return -1;

    return 0;
}

/* dfs */
int dfs(Graph *graph, List *ordered)
{
    DfsVertex *vertex;
    ListElmt *element;

    /* Initialize all of the vertices in the graph. */
    for(element = list_head(&graph_adjlists(graph)); element != NULL; element = list_next(element))
    {
        vertex = ((AdjList *)list_data(element))->vertex;
        vertex->color = white;
    }

    /* Perform depth-first search. */
    list_init(ordered, NULL);

    for(element = list_head(&graph_adjlists(graph)); element != NULL; element = list_next(element))
    {
        /* Ensure that every component of unconnected graphs is searched. */
        vertex = ((AdjList *)list_data(element))->vertex;

        if(vertex->color == white)
        {
            if(dfs_main(graph, (AdjList *)list_data(element), ordered) != 0)
            {
                list_destroy(ordered);
                return -1;
            }
        }
    }

    return 0;
}