代价函数和反向传播
代价函数
首先引入一些新的我们即将讨论的变量名称:
- L = 网络的总层数
- sj s j = 网络第 j 层的单元节点数(不包含偏置项)
- K = 最后一层输出的单元数
- m = 样本的个数
在神经网络中,我们可能有很多输出节点,我用
hθ(x)k
h
θ
(
x
)
k
表示
kth
k
t
h
的输出。逻辑回归中,我们只有一个输出 y,因此 K = 1,回顾正则化逻辑回归的代价函数:
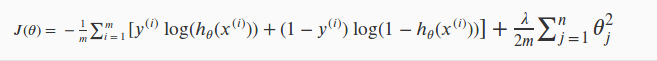
对于神经网络而言,我们的输出一般会大于等于2个节点,因此它的代价函数会比较复杂,如下表示:
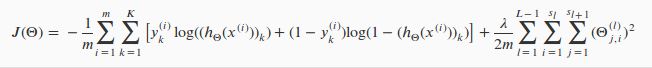
这个看起来复杂很多的代价函数背后的思想还是一样的,方程的第一部分,在方括号之前,我们有一个嵌套求和,主要是将输出层的每个单元的逻辑回归代价都加起来;正则化部分,除了
θ0
θ
0
外,将每一层的每一项
θ
θ
平方再相加。
总结:
- 双重总和只是将输出层中每个单元计算的逻辑回归成本相加
- 三重总和只是将整个网络中所有单个Θ的平方加起来。
反向传播算法
反向传播算法(BP)是神经网络中用来最小化我们的代价函数的一个术语,跟我们前面讲逻辑线性回归模型用梯度下降的方法一样,最终的目的都是:mini
θ
θ
J(
θ
θ
),求它的极值一样通过求它的偏导:
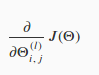
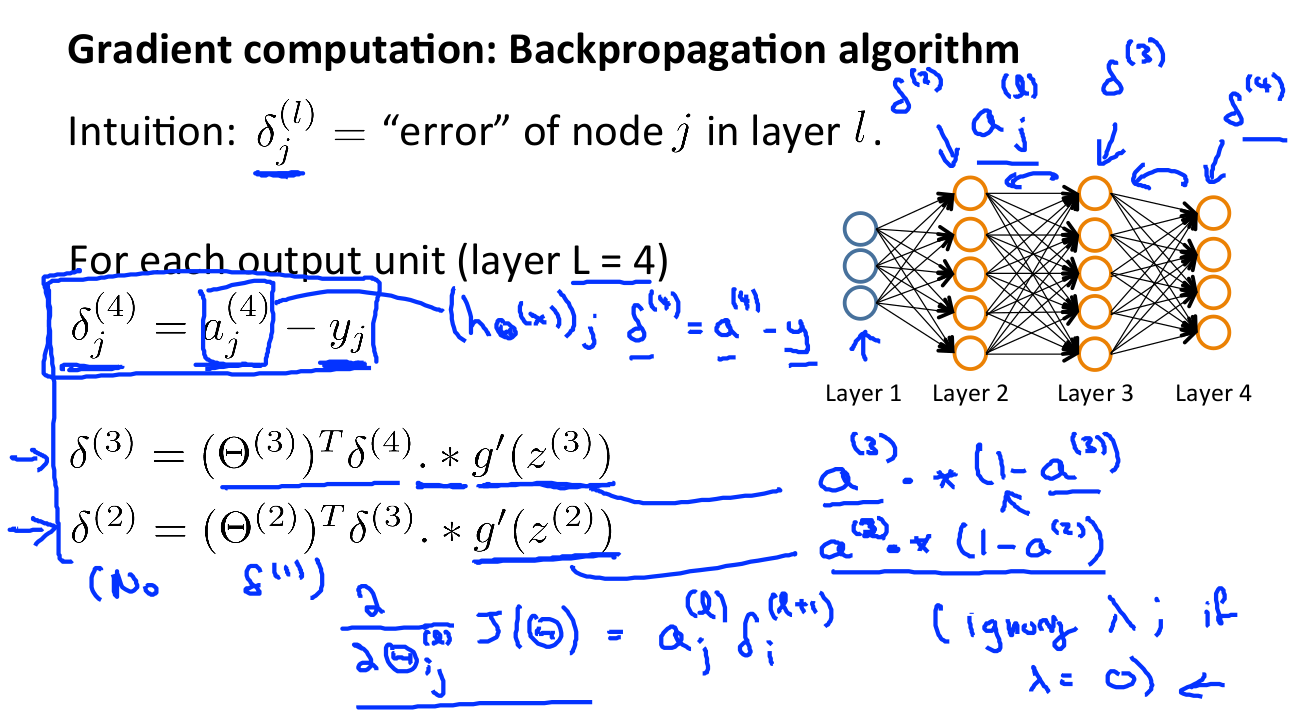
上面的几个公式还是比较难理解的,不过不要急,仔细阅读:https://www.zhihu.com/question/24827633/answer/91489990,阅读后,你应该能明白这些公式的来龙去脉。
BP算法流程如下:

更详细的流程:
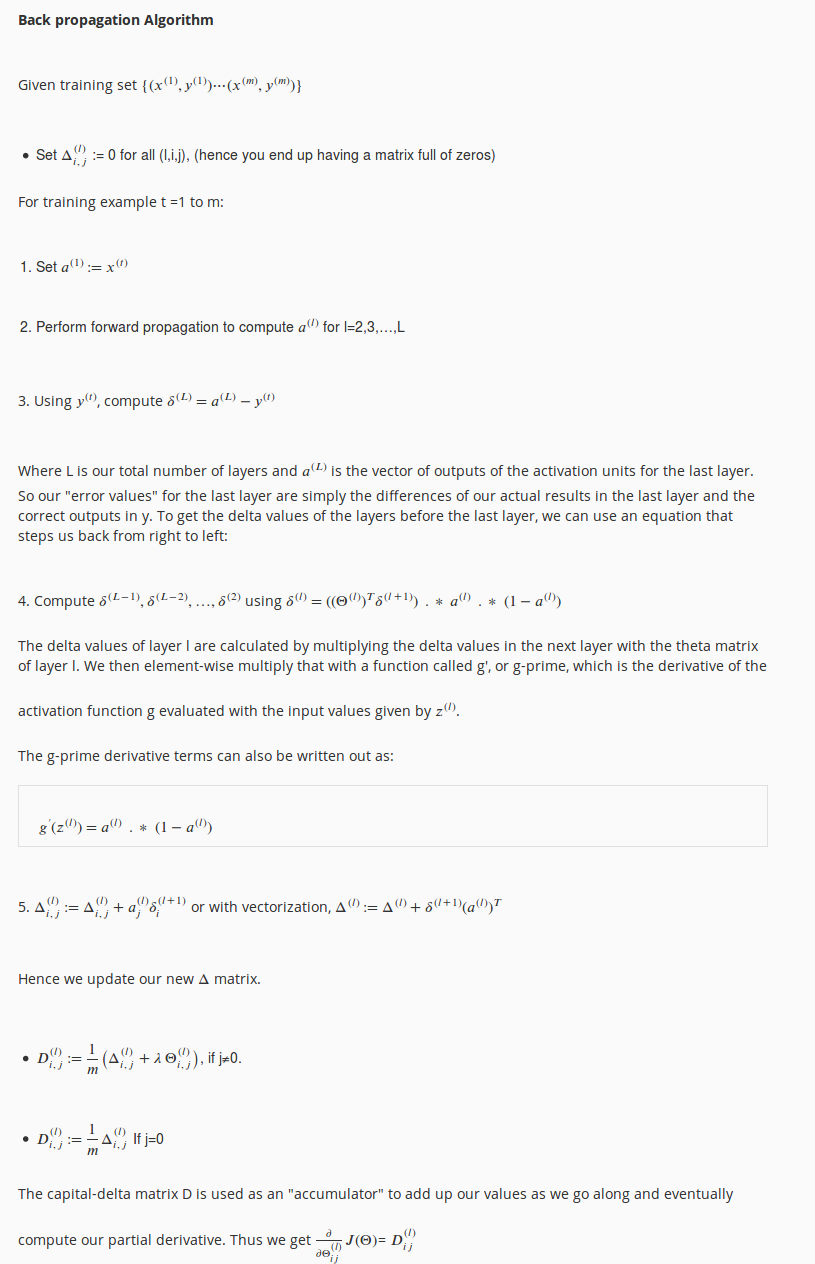
另外这里可以参考:
【1】A Step by Step Backpropagation Example
【2】Unsupervised Feature Learning and Deep Learning Tutorial
尤其是2,建议阅读下,会帮助你理解 BP 算法。
反向传播算法的直观理解
建议直接看A Step by Step Backpropagation Example或知乎上的翻译版https://www.zhihu.com/question/24827633/answer/91489990。
梯度检验
梯度检验会确保我们的BP算法是正常工作的,因为我们对一个复杂模型做梯度下降时,难免存在一些比较难没有发现的bug,导致梯度下降失效,等会过头来发现bug时,时间白白浪费了,为了避免这个问题,我们可以采用一种 Numerical Gradient Checking 的方法来检验我们计算的偏导数是否是正确的。
对梯度的估计采用的方法是在代价函数上沿着切线的方向选择离两个非常近的点然后计算两个点的平均值用以估计梯度。即对于某个特定的
θ
θ
,我们计算出在
θ
θ
-
ϵ
ϵ
处和
θ
θ
+
ϵ
ϵ
的代价值(
ϵ
ϵ
是一个非常小的值,通常选取 0.001),然后求两个代价的平均,用以估计在
θ
θ
处的代价值。
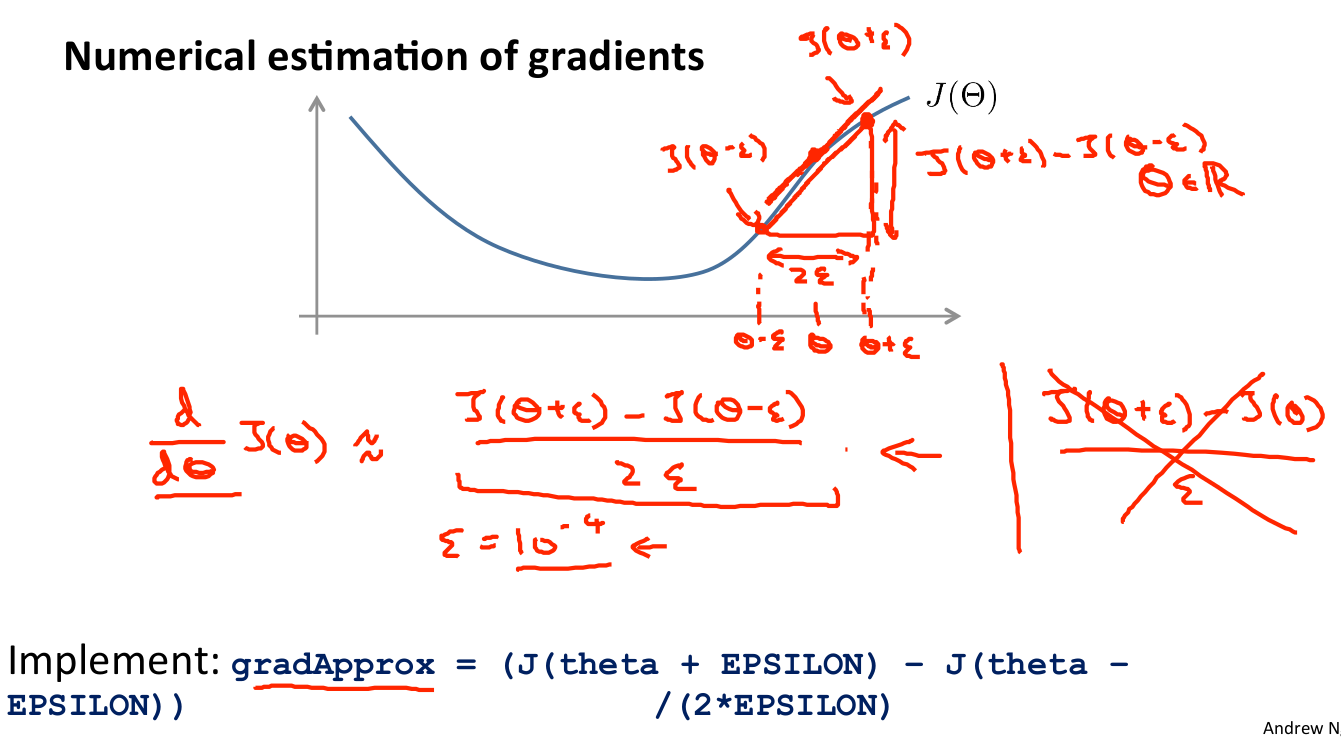
如果
θ
θ
是个向量时,则用如下公式计算,这个公式不难理解。
随机初始化
任何优化算法都需要一些初始的参数。到目前为止我们都是初始所有参数为0,这样的初始方法对于逻辑回归来说是可行的,但是对于神经网络来说是不可行的。如果我们令所有的初始参数都为0,这将意味着我们第二层的所有激活单元都会有相同的值。同理,如果我们初始所有的参数都为一个非0的数,结果也是一样的。
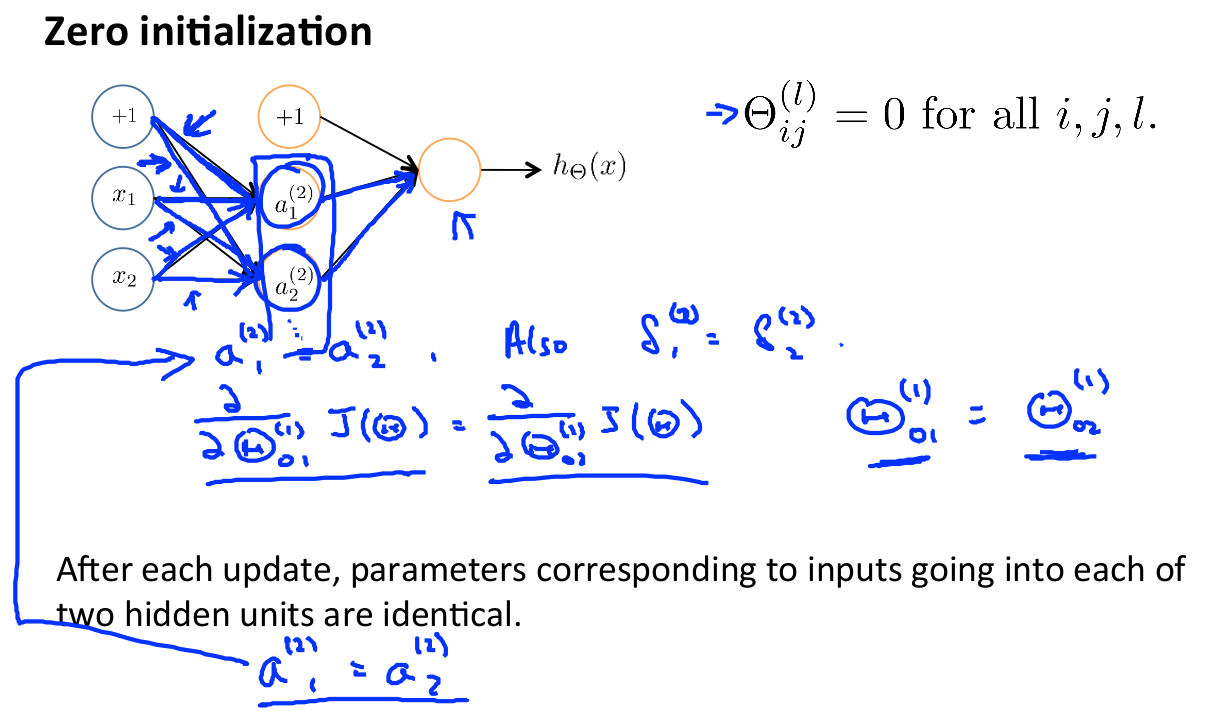
这种线性叫对称现象,我们要打破对称,一般是采用随机初始化权重参数
θ
θ
, 通常初始参数为正负ε之间的随机值,假设我们要随机初始一个尺寸为10×11的参数矩阵,代码如下:
Theta1 = rand(10, 11) * (2*eps) – eps
总结
小结一下使用神经网络时的步骤:
网络结构:第一件要做的事是选择网络结构,即决定选择多少层以及决定每层分别有多少个单元。
第一层的单元数即我们训练集的特征数量。
最后一层的单元数是我们训练集的结果的类的数量。
如果隐藏层数大于1,确保每个隐藏层的单元个数相同,通常情况下隐藏层单元的个数越多越好。
我们真正要决定的是隐藏层的层数和每个中间层的单元数。
训练神经网络:
- 参数的随机初始化
- 利用正向传播方法计算所有的
- 编写计算代价函数 的代码
- 利用反向传播方法计算所有偏导数
- 利用数值检验方法检验这些偏导数
- 使用优化算法来最小化代价函数








 本文介绍了神经网络中的代价函数,包括逻辑回归的代价和神经网络的复杂代价函数,解释了反向传播算法及其直观理解,并强调了梯度检验在验证算法正确性中的重要性。同时,提到了随机初始化参数对于打破神经网络对称性的重要性。
本文介绍了神经网络中的代价函数,包括逻辑回归的代价和神经网络的复杂代价函数,解释了反向传播算法及其直观理解,并强调了梯度检验在验证算法正确性中的重要性。同时,提到了随机初始化参数对于打破神经网络对称性的重要性。
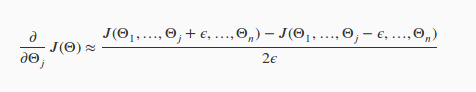














 4946
4946

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








