问题的描述:
有一个一维的无限长棋盘,在棋盘的若干位置上有棋子,每个棋子都能够向棋盘头的方向移动但是不能越过它前面的棋子。问:在给定棋子个数和每个棋子位置的情况下,一共有多少种不同的棋子位置的组合。
解题的思路:
考虑如下情况:
将棋盘从头开始按顺序编号1,2,3....。假设一共有n个棋子,第n个棋子在第m个位置上。这样我们会发现,第n个棋子能够在的合法位置是n到m。分别考虑这m-n+1种情况,则问题化简到分别考虑这些情况下n-1个棋子的可能组合数量。这种n到n-1的递推自然想到了两种算法,递归和动态规划。这里进对动态规划进行讨论。
动态规划的实现:
初始化
为了记录1个棋子到n个棋子的不同组合情况,建立一个二维矩阵。现假设两维分别为x维和y维。x维表示棋子的数目,y维表示棋盘的格子位置。再假设第一个棋子在第k个位置上。
将矩阵初始化如下
递推公式
考虑如下情况,当第n个棋子固定在第i位时,可能的组合数量是第n-1个棋子在第1个位置到第i-1个位置的可能组合数量之和。再进一步考虑,第n个棋子在第i-1位置时,可能的组合情况是第n-1个棋子在第1个位置到第i-2个位置的可能组合数量之和。也就是说,第n个棋子的在第i个位置上的组合情况数量是第n个棋子在i-1位置上的组合的数量加上第n-1个棋子在i-1位置上的组合数量。由上,得到了递推公式:
得到结果
将最后一列相加即可得到结果
C++的简单实现:
#include <iostream>
using namespace std;
int main()
{
//输入总共棋子个数
int count = 0;
cin >> count;
//建立棋子位置一维数组
int *a = new int[count];
//输入棋子起始位置
for(int i = 0; i != count; i++)
{
cin >> a[i];
}
int a_Max = a[count - 1];
//二维动态规划矩阵
int **b = new int*[count];
for(int i = 0; i < count; i++)
{
b[i] = new int[a_Max];
}
//初始化对角线
for(int i = 0; i < count; i++)
{
for(int j = 0; j < a_Max; j++)
{
if(j == i)
{
b[i][j] = 1;
}
else
{
b[i][j] = 0;
}
}
}
//初始化第一列
for(int i = 0; i < a[0]; i++)
{
b[0][i] = 1;
}
//开始
for(int i = 1; i < count; i++)
{
for(int j = i + 1; j < a[i]; j++)
{
b[i][j] = b[i - 1][j - 1] + b[i][j - 1];
}
}
//输出最终结果
int sum = 0;
//将最后一列求和
for(int i = 0; i < a_Max; i++)
{
sum += b[count - 1][i];
}
cout << "sum:" <<sum;
//删除new的空间
delete []a;
a = NULL;
for(int i = 0; i < count; i++)
{
delete []b[i];
b[i] = NULL;
}
delete []b;
b = NULL;
return 0;
}







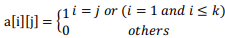
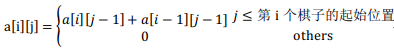














 3117
3117

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








